2024年07月31日
計算が遅い子、計算が速すぎる子。
毎日暑いので、画像は、小仏城山の名物かき氷。
数学を個別指導していて、結果を出すにはかなり時間がかかりそうだと感じるのは、まず、数学の問題を解くのがとても遅い子の場合です。
なぜこんなに時間がかかるのだろう?というほどに解くのが遅いのです。
90分で問題集が1ページ終わらない、ということもあります。
わざとやっている場合もあるのでしょう。
勉強したくない。
沢山問題を解かされたら、損だ。
そういう気持ちが背景にある場合、問題を解くのにのろのろと時間がかかります。
しかし、そういう子も、テストのときは問題を速く解こうとします。
ただ、普段から速く解く練習をしていませんから、テストのときだけ無理をすることになります。
式を丁寧に書かず、暗算をしがちです。
当然、計算ミスが増えます。
テストの結果はあまりよくありません。
ますます勉強する気がなくなります。
練習のときから全力を出していれば、答案を書くスピードも、計算するスピードも上がっていきます。
でも、そういう助言を受けても、やる気がしない。
勉強したくない。
宿題だけは、仕方ないから、やるけど・・・。
テスト前だけは、まあ勉強するけど・・・。
近年、そういう子は、中学受験のボリュームゾーンに多く存在します。
そうして、そのまま中高一貫校の中で温存されていくことがあります。
無理な中学受験で、すっかり学習意欲をなくしてしまったのでしょう。
一方、それ以外ではあまり見かけなくなった気がします。
公立中学の生徒は、真面目で一所懸命な子が多いように感じるのです。
ただし、私立の子も、高校生になればさすがにシャンとしてきます。
一般入試で大学受験するのは嫌だ。
中学受験が本当に本当につらかったから、もうあんな思いはしたくない。
学校推薦か総合型選抜か内部進学で大学に行きたい。
それならば、高校の評定が重要。
そういう判断はできるのです。
そうしてシャンとした後は、問題ありません。
私立の定期テストは、今はとても簡単なことが多いので、本気で勉強すれば何とかなります。
そうではなく、わざとやっているわけではないのに、それでも計算が遅い。
一所懸命だけれど、数学の問題を解くのが遅い。
全力を出しているけれど、遅い。
そういう場合もあります。
計算というのは、ある程度暗記です。
かけ算の九九が代表ですが、たし算・ひき算も、現実には暗記で処理していることがほとんどです。
6+8=14
という計算を、実際に、
「6はあと4をたすと10になるから、1上がって、8から4をひいて4だから、答は14」
とやっているのは、小学校の低学年まででしょう。
6+8=14であることは、今までさんざん計算してきてわかっていること。
だから、もうそれを見た瞬間に、6+8=14 と処理するのが、計算の速い人のやり方です。
しかし、計算が遅い人は、中学生になっても高校生になっても、
6+8=14
を上のような作業をして計算している可能性があります。
あるいは、暗記した計算結果を書こうとはしているが、思い出すのに時間がかかるのかもしれません。
6+8の答は、14だったか、12だったか、何だか自信がなく、どっちだろう、どっちだろう、と考えている時間が、長い。
ペンを持ったまま、計算結果を書くのをためらっている時間の長さは、様子を見ている私からは随分長いなと感じるのですが、本人にとっては一瞬なのだと思います。
計算時間で大差が表れるのは、分数の計算です。
分数の約分や通分は、小学校だけで終わる作業ではなく、中学生になっても高校生になっても、大きく影響します。
高校1年になって、数A「場合の数と確率」の学習をした際に。
考え方が理解できないわけではないけれど、約分にひどく時間がかかるうえに正解が出ない。
高校2年になって、数Ⅱ「積分法」を学習した際に。
やり方を理解できないわけではないけれど、通分に異様に時間がかかるうえに、正解が出ない。
そういうこともあります。
例えば、48/96=1/2 を一度で処理できない。
約分しろと言われると、2で割って、2で割って、2で割って、を繰り返してしまう・・・。
あるいは、48/96をまず6で約分するなど、できるのならば止めないが、何だかちょっとそれは面倒くさくない?と感じる数字を選びがちで、結果、計算ミスをする。
また、通分でいえば、
13/27-5/9+2/3
といった計算に、本当に時間がかかり、しかも、しばしば間違える・・・。
訓練によって獲得するにしろ、生来のセンスであるにしろ、計算力がないと問題を解くのに時間がかかります。
これは、なかなか解消できません。
一所懸命頑張っているけれど、どうしても遅い。
どうやらそれが現状の全力。
それは、見ていればわかります。
全力で頑張っている子に「急げ」と命じ、焦らせたところで、ミスが増えるだけです。
一方、計算だけは異様に速い子も、それはそれで課題を抱えている場合もあります。
おそらく、小学生の頃に計算に特化した訓練を受けたのだと思います。
計算だけはとにかく速い。
ただ、数学的な考え方の理解がそれに追いついていないことがあります。
つまりは、計算しかできない。
人間電卓みたいになってしまっているのです。
そうなると、じっくり分析したり考えたりしなければならない文章題に対しても、計算のときと同じように瞬時に解決しようとすることがあります。
じっくり分析すべき課題を瞬時に解く・・・。
つまりは、「あてずっぽう」で解くのです。
あるいは、式は、問題集の解答解説をすぐ見てしまいます。
式さえ立てば、後は瞬時に計算できます。
計算は速くて正確だから、その点は褒められる。
計算は自分でやっているのだから、これは自分で解いた問題。
算数・数学はそれで大丈夫であるような誤解を本人はしてしまうのかもしれません。
自分が得意なことは重要なことであるというようなバイアスもかかるので、「数学=計算」という間違った観念にとりつかれていることもあります。
テストでは、正しい式を自分で立てられないので、残念な結果となってしまうのです。
なぜ、数学的思考力を同時に伸ばすことができなかったのだろう・・・。
ただ、もし私が小学校の低学年の頃から指導したとしても、同じようになってしまう可能性はあるのです。
周りの大人の誰が悪い、ということはないのです。
結局、どんなに幼くても、子ども自身が判断し選択してしまいます。
計算だけできればいい、解き方だけ覚えればいいと、どこかの段階で、本人が判断してしまうのです。
それを止める手立てが、なかなかないのが実情です。
今年も、全国学力調査の結果が発表され、分析される季節になりました。
日本の子どもたちは、計算能力などの知識・技能は身についている。
しかし、思考力が弱い。
毎度毎度、同じ分析がなされます。
今年は、小学校6年生に出題された、立体に関する文章題が象徴的でした。
直径22㎝の球がぴったり入る立方体の箱の容積を求める問題でした。
そんなの簡単。
22×22×22 で、答は出ます。
しかし、この問題の正答率は37%だったそうです。
22÷3.14などの奇妙な式を立ててしまった子が多かったとのこと。
問題が要求していることを具体的なイメージで理解する力が足りず、記憶の断片をたどって、それらしい計算をしてみた、ということなのかもしれません。
思考する力は、イメージする力。
頭の中だけで上手くいかなければ、実際に手で描いて考えてみる力。
問題に図があるのならば、そこに積極的に数値を書き込んでいく力。
そういうことのできる子が、少ないのです。
手を使って何か描いて考えるということが、できない子が多いです。
高校数学が得意な子は、問題を読みながらすぐ図を描き、あるいはグラフを描きます。
一方、それができない子は、結局、計算問題しか解けません。
純粋な計算問題は、高校数学になるとごく一部です。
模試や入試では、多くて1問か2問しか出題されません。
計算力は必要ですが、計算力だけあっても、壁が立ちふさがります。
考えて問題を解くことができない子。
図やグラフを自分で描くことができない子。
その兆しは、小学生の頃から、もう目に見えて表れています。
普段、考えて算数の問題を解いていないのですから、見たことのない問題に対応することはできないのです。
考えるということが、何をどうすることなのかすら、わからない子もいます。
「自分で考えなさい」
と言われることをひどく嫌う子もいます。
「自分で考えなさい」
「自分で調べなさい」
と言われると、切り捨てられたと感じて、傷ついてしまうようです。
そうではない、ということが、伝わらない・・・。
小学生の頃から、その傾向は見える。
では、それはそのままなのか?
そう決めてかかる必要もありません。
そのままかもしれません。
でも、そうではないかもしれません。
昔、やはりそんな中学受験生がいました。
集団指導塾に通い、うちの教室に補習に来ていた子でした。
「初めて見る問題を、自分で考えろって言うんだよ。習ったことのない問題なんか考えてもわかるわけがないのに」
集団指導塾の授業のやり方を、そのように批判していました。
解き方を覚えるのが勉強。
そう思い込んでいたのでした。
だから、思考力を問われることに腹を立てていました。
これほど弁が立ち、頭のしっかりした子が、こんな考え方なの?
私は、正直、とても驚きました。
しかし、数年後、高校生になって再びうちの教室に通うようになったその子は、かすかにそんな考え方も残り、それで数学の成績がふるわず、再びうちの教室に通うようになったのではありますが、弁が立ち、本質的に頭が良いことも健在でした。
弁が立つ。
それは、自分が何をどうわからないのか、自分が何をどう解釈しているかを語る能力があるということです。
つたない表現でも構わない。
何かを伝えようとしてくれている子には、こちらもやりようがありました。
何がわからないのかを、話しあえる。
数学の問題について、どう解くかを話しあえる。
これは、絶対の強みでした。
会話が可能である限り、勝利への一本道が見えていました。
年月は、多くのことを解決します。
人は成長します。
それを私に学ばせてくれた生徒でした。
数学を個別指導していて、結果を出すにはかなり時間がかかりそうだと感じるのは、まず、数学の問題を解くのがとても遅い子の場合です。
なぜこんなに時間がかかるのだろう?というほどに解くのが遅いのです。
90分で問題集が1ページ終わらない、ということもあります。
わざとやっている場合もあるのでしょう。
勉強したくない。
沢山問題を解かされたら、損だ。
そういう気持ちが背景にある場合、問題を解くのにのろのろと時間がかかります。
しかし、そういう子も、テストのときは問題を速く解こうとします。
ただ、普段から速く解く練習をしていませんから、テストのときだけ無理をすることになります。
式を丁寧に書かず、暗算をしがちです。
当然、計算ミスが増えます。
テストの結果はあまりよくありません。
ますます勉強する気がなくなります。
練習のときから全力を出していれば、答案を書くスピードも、計算するスピードも上がっていきます。
でも、そういう助言を受けても、やる気がしない。
勉強したくない。
宿題だけは、仕方ないから、やるけど・・・。
テスト前だけは、まあ勉強するけど・・・。
近年、そういう子は、中学受験のボリュームゾーンに多く存在します。
そうして、そのまま中高一貫校の中で温存されていくことがあります。
無理な中学受験で、すっかり学習意欲をなくしてしまったのでしょう。
一方、それ以外ではあまり見かけなくなった気がします。
公立中学の生徒は、真面目で一所懸命な子が多いように感じるのです。
ただし、私立の子も、高校生になればさすがにシャンとしてきます。
一般入試で大学受験するのは嫌だ。
中学受験が本当に本当につらかったから、もうあんな思いはしたくない。
学校推薦か総合型選抜か内部進学で大学に行きたい。
それならば、高校の評定が重要。
そういう判断はできるのです。
そうしてシャンとした後は、問題ありません。
私立の定期テストは、今はとても簡単なことが多いので、本気で勉強すれば何とかなります。
そうではなく、わざとやっているわけではないのに、それでも計算が遅い。
一所懸命だけれど、数学の問題を解くのが遅い。
全力を出しているけれど、遅い。
そういう場合もあります。
計算というのは、ある程度暗記です。
かけ算の九九が代表ですが、たし算・ひき算も、現実には暗記で処理していることがほとんどです。
6+8=14
という計算を、実際に、
「6はあと4をたすと10になるから、1上がって、8から4をひいて4だから、答は14」
とやっているのは、小学校の低学年まででしょう。
6+8=14であることは、今までさんざん計算してきてわかっていること。
だから、もうそれを見た瞬間に、6+8=14 と処理するのが、計算の速い人のやり方です。
しかし、計算が遅い人は、中学生になっても高校生になっても、
6+8=14
を上のような作業をして計算している可能性があります。
あるいは、暗記した計算結果を書こうとはしているが、思い出すのに時間がかかるのかもしれません。
6+8の答は、14だったか、12だったか、何だか自信がなく、どっちだろう、どっちだろう、と考えている時間が、長い。
ペンを持ったまま、計算結果を書くのをためらっている時間の長さは、様子を見ている私からは随分長いなと感じるのですが、本人にとっては一瞬なのだと思います。
計算時間で大差が表れるのは、分数の計算です。
分数の約分や通分は、小学校だけで終わる作業ではなく、中学生になっても高校生になっても、大きく影響します。
高校1年になって、数A「場合の数と確率」の学習をした際に。
考え方が理解できないわけではないけれど、約分にひどく時間がかかるうえに正解が出ない。
高校2年になって、数Ⅱ「積分法」を学習した際に。
やり方を理解できないわけではないけれど、通分に異様に時間がかかるうえに、正解が出ない。
そういうこともあります。
例えば、48/96=1/2 を一度で処理できない。
約分しろと言われると、2で割って、2で割って、2で割って、を繰り返してしまう・・・。
あるいは、48/96をまず6で約分するなど、できるのならば止めないが、何だかちょっとそれは面倒くさくない?と感じる数字を選びがちで、結果、計算ミスをする。
また、通分でいえば、
13/27-5/9+2/3
といった計算に、本当に時間がかかり、しかも、しばしば間違える・・・。
訓練によって獲得するにしろ、生来のセンスであるにしろ、計算力がないと問題を解くのに時間がかかります。
これは、なかなか解消できません。
一所懸命頑張っているけれど、どうしても遅い。
どうやらそれが現状の全力。
それは、見ていればわかります。
全力で頑張っている子に「急げ」と命じ、焦らせたところで、ミスが増えるだけです。
一方、計算だけは異様に速い子も、それはそれで課題を抱えている場合もあります。
おそらく、小学生の頃に計算に特化した訓練を受けたのだと思います。
計算だけはとにかく速い。
ただ、数学的な考え方の理解がそれに追いついていないことがあります。
つまりは、計算しかできない。
人間電卓みたいになってしまっているのです。
そうなると、じっくり分析したり考えたりしなければならない文章題に対しても、計算のときと同じように瞬時に解決しようとすることがあります。
じっくり分析すべき課題を瞬時に解く・・・。
つまりは、「あてずっぽう」で解くのです。
あるいは、式は、問題集の解答解説をすぐ見てしまいます。
式さえ立てば、後は瞬時に計算できます。
計算は速くて正確だから、その点は褒められる。
計算は自分でやっているのだから、これは自分で解いた問題。
算数・数学はそれで大丈夫であるような誤解を本人はしてしまうのかもしれません。
自分が得意なことは重要なことであるというようなバイアスもかかるので、「数学=計算」という間違った観念にとりつかれていることもあります。
テストでは、正しい式を自分で立てられないので、残念な結果となってしまうのです。
なぜ、数学的思考力を同時に伸ばすことができなかったのだろう・・・。
ただ、もし私が小学校の低学年の頃から指導したとしても、同じようになってしまう可能性はあるのです。
周りの大人の誰が悪い、ということはないのです。
結局、どんなに幼くても、子ども自身が判断し選択してしまいます。
計算だけできればいい、解き方だけ覚えればいいと、どこかの段階で、本人が判断してしまうのです。
それを止める手立てが、なかなかないのが実情です。
今年も、全国学力調査の結果が発表され、分析される季節になりました。
日本の子どもたちは、計算能力などの知識・技能は身についている。
しかし、思考力が弱い。
毎度毎度、同じ分析がなされます。
今年は、小学校6年生に出題された、立体に関する文章題が象徴的でした。
直径22㎝の球がぴったり入る立方体の箱の容積を求める問題でした。
そんなの簡単。
22×22×22 で、答は出ます。
しかし、この問題の正答率は37%だったそうです。
22÷3.14などの奇妙な式を立ててしまった子が多かったとのこと。
問題が要求していることを具体的なイメージで理解する力が足りず、記憶の断片をたどって、それらしい計算をしてみた、ということなのかもしれません。
思考する力は、イメージする力。
頭の中だけで上手くいかなければ、実際に手で描いて考えてみる力。
問題に図があるのならば、そこに積極的に数値を書き込んでいく力。
そういうことのできる子が、少ないのです。
手を使って何か描いて考えるということが、できない子が多いです。
高校数学が得意な子は、問題を読みながらすぐ図を描き、あるいはグラフを描きます。
一方、それができない子は、結局、計算問題しか解けません。
純粋な計算問題は、高校数学になるとごく一部です。
模試や入試では、多くて1問か2問しか出題されません。
計算力は必要ですが、計算力だけあっても、壁が立ちふさがります。
考えて問題を解くことができない子。
図やグラフを自分で描くことができない子。
その兆しは、小学生の頃から、もう目に見えて表れています。
普段、考えて算数の問題を解いていないのですから、見たことのない問題に対応することはできないのです。
考えるということが、何をどうすることなのかすら、わからない子もいます。
「自分で考えなさい」
と言われることをひどく嫌う子もいます。
「自分で考えなさい」
「自分で調べなさい」
と言われると、切り捨てられたと感じて、傷ついてしまうようです。
そうではない、ということが、伝わらない・・・。
小学生の頃から、その傾向は見える。
では、それはそのままなのか?
そう決めてかかる必要もありません。
そのままかもしれません。
でも、そうではないかもしれません。
昔、やはりそんな中学受験生がいました。
集団指導塾に通い、うちの教室に補習に来ていた子でした。
「初めて見る問題を、自分で考えろって言うんだよ。習ったことのない問題なんか考えてもわかるわけがないのに」
集団指導塾の授業のやり方を、そのように批判していました。
解き方を覚えるのが勉強。
そう思い込んでいたのでした。
だから、思考力を問われることに腹を立てていました。
これほど弁が立ち、頭のしっかりした子が、こんな考え方なの?
私は、正直、とても驚きました。
しかし、数年後、高校生になって再びうちの教室に通うようになったその子は、かすかにそんな考え方も残り、それで数学の成績がふるわず、再びうちの教室に通うようになったのではありますが、弁が立ち、本質的に頭が良いことも健在でした。
弁が立つ。
それは、自分が何をどうわからないのか、自分が何をどう解釈しているかを語る能力があるということです。
つたない表現でも構わない。
何かを伝えようとしてくれている子には、こちらもやりようがありました。
何がわからないのかを、話しあえる。
数学の問題について、どう解くかを話しあえる。
これは、絶対の強みでした。
会話が可能である限り、勝利への一本道が見えていました。
年月は、多くのことを解決します。
人は成長します。
それを私に学ばせてくれた生徒でした。
2024年07月24日
英語長文を何とか読み進めていく力。

例えば、以下のような長文を読むときに。
A consumer walks into a store. They stands in front of hundreds of boxes of laundry detergent. They chooses one brand, pays for it, and leaves. Why dose they pick that specific kind of soap? Is it truly better than the others? Probably not. These days, many products are nearly identical to one another in quality and price. If products are almost the same, what makes consumers buy one brand instead of another? Although we might not like to admit it, commercials and advertisements probably influence us much more than we think they do.
問 下線部の it が表す内容を、句読点を含めて30字以内で述べよ。
さて、繰り返し述べてきていることですが、高校生として知っておくべき基本単語が身についていないために英語長文が読めない場合は、まず単語力強化が課題です。
上の文章で言えば、consumer , product , quality , price , admit , commercials , advertisement などの単語の意味が1つもわからない場合は、この文章は読めません。
わからない単語がある中でも何とか文意を取って問題に正解していく、というのにも限界がありますので、高校生として知っておくべき基本単語は覚えましょう。
さすがに、それくらいは、わかる。
でも、他にわからない単語があるので、もやもやする。
そういう生徒と授業をしていたときのこと。
さて、まず第1文。
A consumer walks into a store.
「わからない単語は、ありますか」
「ありません」
「はい。では、日本語にしてみてください」
「消費者が、店に歩いて入っていく」
「はい。すばらしい」
第1文から、論を展開される文章も意味がとりづらいですが、このように、具体的な話から文章が始まるのも、違和感が強くて、どう読んでいいかわからない、という人がいます。
これは、とにかく慣れが必要です。
そういう書き方の文章もあるんだな、と慣れてしまうことです。
続く第2文。
They stands in front of hundreds of boxes of laundry detergent.
「この they は大丈夫ですか。1文目の主語が a consumer だったので、男か女かわからないんです。少し前は、こういうとき、he or she という代名詞を使いましたが、それも面倒なので、今は、they を使うことがあります。『単数形の they』と呼ばれるものです」
「はい」
「他に、この文で、何かわからない単語はありますか」
「detergent」
「うん。単語集にあまり載っていない単語ですね。品詞は何ですか」
「名詞?」
「はい。では、デタージェントのままで訳してください」
「消費者は、立つ。何百ものランドリー・デタージェントの箱の前に」
「はい。いいですね」
「ランドリー・デタージェントって何ですか」
「では、ランドリーって、何?」
「・・・」
「コイン・ランドリーって、知っている?」
「知りません」
「そうですか・・・」
英語の長文を読み進める際に、日本語の語彙力も重要です。
日本語の語彙が豊かな子ほど有利ではあるのです。
高校生にとっては、コインランドリーはあまり関係がないもの。
生活に密着した言葉ではありません。
自分にあまり関係がないものには関心がない。
知識も語彙も広がらない。
そういうことは、あります。
それでも、自分に全く関係のない文章を読まなければならない・・・。
国語も英語も、文章が読めない子は、そういう弱点を抱えていることがあります。
「まあ、大丈夫。そのままにして、第3文に進みましょう」
They chooses one brand, pays for it, and leaves.
「消費者は1つのブランドを選んで、支払って、去る」
「すばらしい。では、次の文を日本語にしてください」
Why dose they pick that specific kind of soap?
「specific の意味がわかりません」
「じゃあ、スペシフィックのままで」
「なぜ、消費者は、あのスペシフィックで親切な石鹸を刺したのか?」
「お?」
わからないことがたまっていくと、やがて訳が崩れていく・・・。
そして、意味が取れなくなっていく。
そのようなことはよくあります。
「じゃあ、もうスペシフィックを飛ばして、that kind of soap として訳してみよう」
「・・・あ。なぜ消費者は、あの種類の石鹸を刺したのか?」
「刺したんですかね?前の文から推測しましょう。話は急に飛んだりはしないです。2文前で、この消費者は何をしました?」
「1つのブランドを選んで、支払って、去る」
「ですよね。じゃあ、刺してないよね?」
「・・・選んだ?」
「そう。ピックアップと考えるとわかりやすいかな?」
「ああ・・・」
「1つのブランドを選んだんですね。ブランドってわかる?」
「何となく・・・」
「何のブランドを選んだんでしょうか」
「ランドリー・デタージェント」
「はい。そうそう。それは、今の文で、どう言い換えられていますか?」
「え?」
英語は、同じ単語を極力使わないようにする言語です。
同じ表現ばかり使う人は、文章を書くのが下手な人。
教養のない人。
そう思われるので、日本人の感覚からすれば異様なほどに言い換えます。
それを前提に英文を読んでいくことが必要です。
その前提を理解しないまま英文を読む人は、読んでいてすぐに迷子になってしまいますし、四択問題などで、本文と同じ表現のひっかけの選択肢に簡単にだまされます。
英文は、同じことを別の言葉でどんどん言い換えていくのです。
選択肢も、基本的には言い換えてあるものが正解です。
本文と同じ表現が使われている選択肢は、フェイクの可能性が高い。
そういう観点で問題を解いていくだけで、正答率が上がります。
「この消費者は、選んだんですよね。何を選んだの?」
「ランドリー・デタージェント」
「うん。それは、今の文で、何と言い換えられていますか?」
「えー・・・。わからない・・・」
「ほお・・・。では、今の文をもう1回訳して」
「なぜ消費者は、その種類の石鹸を選んだのか」
「うん。つまり何を選んだの?」
「・・・石鹸?」
「そうですよ。ランドリー・デタージェントは、石鹸。正しくは、洗濯洗剤のことです」
「ああっ・・・」
「このように、言い換えてあることが多いので、英文を読むときは、諦めないことです。先を読んでいくと、同じことが別の言葉で表現されているから、諦めない。そこを読み取りましょう」
「はあ・・・」
続く文。
Is it truly better than the others?
「それは他よりも、本当に良いのですか」
Probably not.
「多分、違う」
These days, many products are nearly identical to one another in quality and price.
「わからない単語はありますか?」
「identical」
「うん。でも、似たような単語は知っているはずですが。見覚えはありませんか」
「えー・・・」
「identify は?」
「えーと、えーと・・・」
「identification は?」
「えー・・・」
「国語の授業で読んだ文章に、アイデンティティという単語は出てきませんでしたか?評論でよく使われる単語なので、知っておかないとまずいはずですが」
「よくわかりません・・・」
「では、identical の品詞は?」
「多分、形容詞?」
「はい。それでは、アイデンティカルのままで、文全体の意味を取ると?」
「この頃、多くの製品は、近くアイデンティカルだ。お互いに。質と価格で」
「うん。まあいいですよ。では、次の文の意味は?」
If products are almost the same, what makes consumers buy one brand instead of another?
「もし製品がほとんど同じならば、何が消費者に買わせるのか。1つのブランドを。他の代わりに」
「すばらしい。よく勉強しています。そして、これも、前の文を言い換えていますね。nearly identical の言い換えは、この文のどこかな?」
「あ。 almost the same」
「そうです。こういう言い換えに乗っていけば、少しくらいわからなくても、読み進めていけるんです」
「はあ・・・」
「でも覚えていたほうがより楽に英文を読んでいけます。identify は、『同じものと考える , 同一視する』という意味の動詞。identification は、同一であることの証明、すなわち『身分証明書』という意味の名詞。IDというのはその頭文字です。identity は、自己同一性。すなわち、自分らしさ。自分であることの根拠。よりどころ」
「はあ・・・」
「覚えましょう。他の英文でもよく出てきます。こういう単語は、覚えておけば得をします。多くの文章で出てくるこういう単語は、覚えましょう。単語集に載っている単語は、そういう単語です」
「はい」
「では、次の文の意味は?」
Although we might not like to admit it, commercials and advertisements probably influence us much more than we think they do.
「私たちはそれを認めることが好きではないかもしれないのではあるが、コマーシャルと広告は、多分影響する。私たちに。私たちが思っているよりも」
「すばらしいです。では問題を解きましょう。下線部の it の内容は?」
「1つのブランド?」
「・・・え?」
ここまで読み取っているのに、問題が解けない・・・。
代名詞の指示内容を把握できない。
おそらく、国語も苦手なのだろうと思うのです。
読書習慣がないからだろうなあと根本の原因は容易に思いつくのですが、もう高校生になっていて、今更読書をするわけがない。
文字を読むのは勉強をするときか、スマホを見るときだけ。
指示語の指示内容を読み取らねばならない文章がスマホに出てくるわけがないので、国語が苦手な子は、勉強しない限りは国語が苦手なままです。
そして、とても安易な勉強をしてしまうことがあります。
上の子の間違いは、「指示語の指示内容は、直前に書いてある」という思い込みから発生していました。
it に当たる単数名詞を前の文で探したら、one brand が見つかった。
そういうことだったのでした。
そうやって、機械的に解いていくことでもある程度は正解するのですが、そういう読み取りをしているということは、もしかしたら、文章の意味は全く理解できていないのではないか?
そのような気配も感じて不安になるのです。
Although we might not like to admit it, commercials and advertisements probably influence us much more than we think they do.
「私たちはそれを認めることが好きではないかもしれないのではあるが、コマーシャルと広告は、多分影響する。私たちに。私たちが思っているよりも」
「さきほどの訳、すばらしかったですよ。その意味をよく考えてください。『それ』の中身は何でしょうか」
「・・・」
「国語の文章もそうなんですが、『それ』の中身は、前の文に書かれているとは限らないのです。『それ』の後ろに中身が書かれていることも、たまにあるんですよ」
「ええっ」
「機械的に解くのではなく、意味を理解すれば、わかるんです」
「えー・・・」
「私たちは文章を読んでいるのですから、文章の意味を理解しましょう」
「解き方とか、ないんですか」
「うーん・・・。この文の although 節は従属節ですから、主節の後ろに書くこともできます。だから、本来後ろにあった it が前に来たのだという解釈はできますが、そんな解釈は、むしろ面倒くさいと思います。『それ』の中身を『1つのブランド』だとして、それで文の意味が通るかどうかを確認すると何か変だなと感じることのほうが簡単だと思いますよ」
「えー・・・」
「指示語の指示内容を答えるときは、元の文に入れてみて、本当に意味が通るかどうかを確認しましょう。結局、小学校の頃からそのように教わっていませんか」
「・・・」
あてはめてみましょう。
「私たちは1つのブランドを認めることが好きではないかもしれないのではあるが、コマーシャルと広告は、多分影響する。私たちに。私たちが思っているよりも」
これは、文脈上、おかしい。
だって、実際は、1つのブランドを認めて選んで、買って帰ったのですから。
「私たちはそれを認めることが好きではないかもしれないのではあるが、コマーシャルと広告は、多分影響する。私たちに。私たちが思っているよりも」
それ、の中身は何でしょうか。
この文の後半の内容ですよね。
これを、30字以内でまとめましょう。
字数制限がある場合は、面倒でも下書きをしたほうが完成度の高い答案を書くことができます。
コマーシャルと広告は
私たちが思っているよ
りも私たちに影響する
ということ。
下書きは、36文字になりました。
さて、何を削るか?
この場合、コマーシャルと広告は、ほぼ同じ内容なので、どうしても2つ書かなければならないものではありません。
「広告は私たちが思っているよりも私たちに影響するということ。(29字)」
これはこれで正解です。
ただし、記述答案の正解は1つではありません。
この下書きでは、私たち、という表現がかぶっています。
ここを削れないかなあ、と考えた場合。
「コマーシャルと広告が思っているよりも私たちに影響すること。(29字)」
この答案は無生物主語なので、いっそ、主語を転換した場合は。
「私たちは思っているよりもコマーシャルと広告に影響されること。(30字)」
などとスラスラと書いてきましたが、こういう推敲が苦手な人は多いです。
記述答案を作ってきた経験がほとんどないのだろうと想像されます。
このように、英語の授業なのに、結局、記述答案作成の授業になってしまうことも多いです。
でも、それも必要なことなのです。
2024年07月18日
復習に力を入れてください。

「夏期講習は、どうせ復習でしょう」
と言われて、これはまずい、と思ったことがありました。
いや、復習も予習も、両方やるのが、夏期講習です。
・・・というか、それ以前に、「どうせ復習」とはどういう意味だったのでしょう。
「どうせ復習」という言葉は、重要なヒントだと思います。
復習中心ではあまり意味がない、ととらえているお母様がいらっしゃるのだということ。
それは、「復習するために塾に通わせるのは、意味がない」ということでしょうか。
復習なら家でできる、と思ってしまうのでしょう。
あるいは、お母様としては講習会に参加させても良いのだが、子どもが行きたがらない。
「どうせ復習だから、講習会は参加しない」と子どもが言い出す・・・。
復習軽視。
予習のために塾に行く。
確かに、生徒には、そういう意識の子が多いです。
塾に一番に期待することは、予習。
とにかく、学校の授業がよくわかるように、予習をしたい。
だから、学校の授業がない夏休みや冬休みに、塾に通う意味はない・・・。
個別指導の場合は、予習が少したまると、学期中の普通の授業日も休んでしまう子すらいます。
塾では、勿論、予習をします。
しかし、予習だけが重要なわけではありません。
成績を上げるために重要なのは、むしろ復習です。
予習・予習と言っている子に、成績の良い子はそんなにいないのです。
学校の授業がよくわからなくて不安だから、予習・予習と思ってしまう気持ちはわかります。
その教科が苦手だから、学校の授業がわかるように予習をしてほしがるのだろうと思います。
その要望には勿論応えます。
しかし、それで成績が上がるわけではありません。
「わかる」だけではダメだからです。
問題を自力で正解できるようにならなければ、成績は上がりません。
決め手は、復習です。
復習のやり方がすべてと言っても過言ではありません。
そして、成績のふるわない子は、復習が下手です。
復習することの価値も意味も気づいていない場合もあります。
小学校の勉強は簡単なので、復習などしなくても、学校の授業と宿題だけで大体は身についてしまいます。
だから、復習が必要だということが実感できないまま中学生になっている子がいます。
復習という概念がない。
復習が自分に必要なことだと思っていないのです。
「わかった」と思った瞬間に、それでOKと思っている子も多いです。
それだけでは問題が解けないことに気づいていないのです。
「わかる」ことと、「自力で問題に正解する」こととの間には、大変な距離があります。
復習することの価値がわかっていなかったら、家でも、復習しません。
自分が一度理解したことは、もう永久に自分の頭の中にある、と誤解しているのです。
だから復習を軽視します。
脳はすべての記憶を簡単に消去していきます。
不要な記憶と判断したら、すぐに消します。
脳のその働きに抗うために、繰り返し繰り返し復習する必要があるということが、わかっていません。
だから、実際に問題を解こうとすると解けないことに、本人が一番驚くのです。
復習のやり方を教わり、復習のための良質の教材をもらい、復習の機会を得るために塾に通うのです。
塾の最大の機能です。
むしろ、予習は、1人でもできるのです。
教科書を一度読んでみる。
読んでみて、わかるようなら、大丈夫です。
わからないようなら、何がわからないのか、チェックしておく。
予習の段階で、そんなに何もかもわかる必要はありません。
授業で理解できればよいのですから。
英語なら、教科書本文の音声を、まずは本文を見ないで聴いてみる。
聴くだけで内容をどこまで理解できるか、確認する。
その後、本文を読む。
わからない単語があれば、下線を引くか、書きだしておく。
文意の取れない部分があれば、それも下線を引く。
その先、単語の意味を調べておくかどうかは、それは、学校の先生の指示に従えばよいでしょう。
数学なら、例題を解いてみる。
解けるようなら、大丈夫。
時間がなければ、例題や解説を読んでおくだけでも大丈夫。
もしわからないのならば、学校の授業で、そこを重点的に聞けばよいのです。
こうした予習は、1人でできます。
しかし、復習は、1人ではできない子が多いのです。
何をどう復習すれば成績が上がるのか、わかっていない。
予習予習と予習に追われて、復習の機会がないまま、気がつくとテスト2週間前という子も多いです。
予習のときは、目がキラキラしている。
新しいことを教わるのは好き。
でも、復習にはあまり興味がない。
復習は、同じことの繰り返しなので、つまらない。
そして、定期テストでぱっとしない点をとっても、何が原因なのか、よくわからない・・・。
・・・いや、復習しないからですよ。
成績の悪い子は、予習の習慣がないのではなく、復習の習慣がないのです。
効果的な復習法を身につけていないのです。
復習しましょう。
何度でも。
2024年07月11日
中学数学。方程式の解き方の根拠。

数学のテストは、計算だけできればそれでいいわけではなく、なぜそのように解くことができるのか、根拠も問われます。
例えば、中1で学習する、1次方程式の場合、単なる計算問題としては。
問題 次の方程式を解け。
3x-5=4
これは簡単ですね。
3x-5=4
3x=9
x=3
はい。正解です。
ところが、定期テストでは、これをただ解く問題だけでなく、どのように解いているのか根拠を問う問題がかなりの頻度で出題されます。
問題 以下の( )にあてはまる数を答えよ。
3x-5=4
両辺に(①)を加えて。
3x=9
両辺を(②)で割って。
x=3
これに全く答えられない子がいます。
方程式を解くことはできるのですが、上のような問題には答えられないのです。
そもそも、この問題が何を要求しているのか理解できない様子で、ポカンとしてしまいます。
次のような問題になると、もっと正答率が下がます。
問題
3x-5=4・・・①
3x=9 ・・・②
x=3 ・・・③
上の①から②の間、②から③の間に使われた等式の性質を以下のア~エから選び、それぞれ記号で答えなさい。
ア. A=Bのとき、A+C=B+C
イ. A=Bのとき、A-C=B-C
ウ. A=Bのとき、AC=BC
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
何を問われているのか、意味がわからない・・・。
そういう子たちがいます。
けれど、その子たちは、方程式を解くことはできるのです。
もっと複雑な方程式でも、解くことはできます。
でも、上のような形式の問題は、正答できないのです。
算数もそうなのですが、数学は、ただ計算ができればそれでいいわけではなく、なぜそのように解くのか、なぜそのように解けるのか、根拠や意味を理解することが大切です。
だから、解き方の根拠を問う問題も定期テストに出題されます。
しかし、そのことを理解せず、解き方を覚えるだけで済ませようとする子は多いです。
解き方を覚えればいいと思いこんでいるので、根拠を問う問題を目にすると、何を答えればいいのかわからないのです。
わからない、というだけでなく、そうした問題に対する反感や抵抗感も強いように感じます。
小学生の頃から、
「やり方だけ教えて」
「やり方だけ知りたい」
ということで算数の勉強を済ませてきた子たちにとっては、それが「正義」です。
正解さえ出していれば責められることはなかったのですから、それでいいと思っていても当然です。
この勉強のやり方で間違いない。
そう思って、中学生になったのです。
それでいいと思っていたら、「方程式の解き方の根拠」という、訳のわからない課題にぶつかってしまいます。
そりゃあ、フリーズしますよね。
繰り返し書いてきていることですが、やり方だけ覚えようとする子は、そのほうが合理的だと誤解しています。
根拠まで理解しようとすると、脳のメモリを余計にくってしまって、重い。
やり方だけ覚えて、テストが終われば忘れてしまったほうが、頭が楽。
本人が意識していなくても、そのような学習習慣が身についてしまっている子は多いです。
そして、解き方の根拠に戻ろうとしても、もう理解できなくなってしまっている場合もあります。
高校数学まで進んで、やり方は覚えきれないし、意味もわからないとなった場合、戻るのは大変な苦労が必要です。
中学1年なら、やり直しは可能。
ここから、根拠を理解する学習を始めましょう。
とはいえ、小学校の6年間で蓄積された学習習慣の打破は、それなりに難しいのですが。
3x-5=4
3x=9
x=3
と簡単に書かれている方程式の答案。
実際に解くだけならば、答案としてはこれで十分なのですが、ここには多くの根拠が隠されています。
まず、なぜ、
3x-5=4
3x=9
となるのでしょうか?
「移項したから」
と答えられる子は、移項という数学用語を使えるだけ賢い子ではあるのですが、ではなぜ移項は可能なのか?
なぜ、左辺の-5は、右辺に移項されると+5になるのか?
そこを説明できるか、できないかが、大きな分岐点です。
「移項するときは符号を変える」
というやり方だけ覚えているのか、それとも、意味がわかっているのか?
3x-5 =4
両辺に5を加えて、
3x-5+5=4+5
3x=9
いちいち書き記さないだけで、実際は、このような作業が行われています。
使われているのは、上の等式の性質のうち、
ア. A=Bのとき、A+C=B+C
です。
等式は、左辺と右辺が等しいという関係を表した式。
左辺と右辺に、それぞれ同じものを加えても、等しい関係は変わらないのです。
その性質を利用して、両辺に5を加えると、-5+5=0となります。
方程式を解くのに邪魔だった左辺の-5を消すことができるのです。
続けて、
3x=9
両辺を3で割って、
x=3
ここで使われている等式の性質は、
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
です。
左辺と右辺を同じもので割っても、等しい関係は変わらない。
その性質を利用しています。
しかし、このような解説を、恐ろしいくらいに理解できない子たちもいます。
それは学力が低いためとは限らないのです。
方程式の解き方自体はスラスラと身につけます。
かなり複雑な、( )を含んでいたり、係数が分数な方程式も。
ところが、上のような根拠を問う問題になると、凝固したようになり、全く話が通じなくなります。
「聞いてますか?」
「わかりますか?」
「どこがわからないですか?」
と繰り返し問いかけても、全く反応がなく、呆然としてしまうのです。
何がわからないのかを説明することもできず、ただ黙り込む。
だから、こちらとしては推測するしかないのですが、考えられることは、上のように、方程式の解き方の根拠を問う問題は、その子の考える「算数・数学の問題」の概念から大きく外れているのではないか?
彼らにとって、そうした問題は、宇宙人の話す宇宙語よりも異様であり、理解の範疇を超えている。
何を問われているのか、全く意味がわからない。
彼らにとっては、やり方を覚えることが算数・数学の学習であり、根拠を問う問題など、算数・数学の問題ではないのでしょう。
その間違った固定観念を打破しないと、上のような問題を理解することができないままかもしれません。
正攻法の説明を繰り返しても全く話が通じないときに、最後の手段を講じることがあります。
「この問題は、テストに出ます。
中学の定期テストはそういうもの。
小学校の算数とは違います」
テストに出るぞ。
テストに出るぞ。
テストに出るぞ。
どう考えても、教育的ではありません。
しっかりと意味を伝えることをまず優先するべきです。
しかし、相手の固定観念があまりにも強く、このままでは膠着状態が続く。
テストが近づいている。
そうしたときに、この最後の手段を講じます。
テストに出るぞ。
このあまりにも打算的な言葉が、意味が通じず凝固していた子には響くことがあるのです。
「やり方だけ覚えればいい」という考え方と、「テストに出るぞ」という考え方は親和性が高いからでしょう。
明らかに表情が変わります。
彼らは、計算のやり方の根拠を問う問題などテストに出るわけがないという、これも間違った固定観念に凝り固まり、そのせいで理解する気がそもそもなかったのかもしれません。
しかし、これがテストに出るのなら、このタイプの問題の「解き方」も覚えなければならないのです。
でも、こういう問題の解き方って・・・?
それは、結局、計算のやり方の意味を理解することになるのです。
正攻法では不可能だった、根拠を考える学習が、この形で可能になることがあります。
もう一度、上の問題を。
問題
3x-5=4・・・①
3x=9 ・・・②
x=3 ・・・③
上の①から②の間、②から③の間に使われた等式の性質を以下のア~エから選び、記号で答えなさい。
ア. A=Bのとき、A+C=B+C
イ. A=Bのとき、A-C=B-C
ウ. A=Bのとき、AC=BC
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
「①から②の間に、等式の性質のどれを利用しているんでしょう?」
「・・・イ?」
「あー・・・、-5を消したのだから、ひき算だと思った?
いや、そうじゃないんですよ。
3x-5+5=4+5
というふうに計算しているんです。だから?」
「・・・エ?」
「・・・何で?」
このような会話を交わすことも多いです。
方程式を解くだけならできる子が、こんなにも理解していないのだと、こうした会話を通してわかります。
その子の中の数学に関する底知れない深淵が垣間見えるようです。
その深淵は、その子が、小学校の6年間で作ってきた深淵。
下手をすると、深淵が広がり、乗っている板1枚の下には何もない状態になってしまいます。
実際、高校数学を学習していて、そのような状態の子もいます。
深淵は知識で埋めていく作業が必要です。
やり方だけ覚えてやり過ごしてきたためにできてしまった深淵は、こんな1問だけで埋まるわけではありませんが、一助にはなります。
学年が上がれば、太郎さんと花子さんが、問題の解き方について、べらべらと1ページ以上も会話する問題も定期テストに出ます。
言うまでもなく、大学入試共通テスト型の問題です。
それは、学校によっては、中学の定期テストから始まります。
意味がわからなければ、太郎さんと花子さんの会話の空欄は埋まりません。
例えば、中1で学習する、1次方程式の場合、単なる計算問題としては。
問題 次の方程式を解け。
3x-5=4
これは簡単ですね。
3x-5=4
3x=9
x=3
はい。正解です。
ところが、定期テストでは、これをただ解く問題だけでなく、どのように解いているのか根拠を問う問題がかなりの頻度で出題されます。
問題 以下の( )にあてはまる数を答えよ。
3x-5=4
両辺に(①)を加えて。
3x=9
両辺を(②)で割って。
x=3
これに全く答えられない子がいます。
方程式を解くことはできるのですが、上のような問題には答えられないのです。
そもそも、この問題が何を要求しているのか理解できない様子で、ポカンとしてしまいます。
次のような問題になると、もっと正答率が下がます。
問題
3x-5=4・・・①
3x=9 ・・・②
x=3 ・・・③
上の①から②の間、②から③の間に使われた等式の性質を以下のア~エから選び、それぞれ記号で答えなさい。
ア. A=Bのとき、A+C=B+C
イ. A=Bのとき、A-C=B-C
ウ. A=Bのとき、AC=BC
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
何を問われているのか、意味がわからない・・・。
そういう子たちがいます。
けれど、その子たちは、方程式を解くことはできるのです。
もっと複雑な方程式でも、解くことはできます。
でも、上のような形式の問題は、正答できないのです。
算数もそうなのですが、数学は、ただ計算ができればそれでいいわけではなく、なぜそのように解くのか、なぜそのように解けるのか、根拠や意味を理解することが大切です。
だから、解き方の根拠を問う問題も定期テストに出題されます。
しかし、そのことを理解せず、解き方を覚えるだけで済ませようとする子は多いです。
解き方を覚えればいいと思いこんでいるので、根拠を問う問題を目にすると、何を答えればいいのかわからないのです。
わからない、というだけでなく、そうした問題に対する反感や抵抗感も強いように感じます。
小学生の頃から、
「やり方だけ教えて」
「やり方だけ知りたい」
ということで算数の勉強を済ませてきた子たちにとっては、それが「正義」です。
正解さえ出していれば責められることはなかったのですから、それでいいと思っていても当然です。
この勉強のやり方で間違いない。
そう思って、中学生になったのです。
それでいいと思っていたら、「方程式の解き方の根拠」という、訳のわからない課題にぶつかってしまいます。
そりゃあ、フリーズしますよね。
繰り返し書いてきていることですが、やり方だけ覚えようとする子は、そのほうが合理的だと誤解しています。
根拠まで理解しようとすると、脳のメモリを余計にくってしまって、重い。
やり方だけ覚えて、テストが終われば忘れてしまったほうが、頭が楽。
本人が意識していなくても、そのような学習習慣が身についてしまっている子は多いです。
そして、解き方の根拠に戻ろうとしても、もう理解できなくなってしまっている場合もあります。
高校数学まで進んで、やり方は覚えきれないし、意味もわからないとなった場合、戻るのは大変な苦労が必要です。
中学1年なら、やり直しは可能。
ここから、根拠を理解する学習を始めましょう。
とはいえ、小学校の6年間で蓄積された学習習慣の打破は、それなりに難しいのですが。
3x-5=4
3x=9
x=3
と簡単に書かれている方程式の答案。
実際に解くだけならば、答案としてはこれで十分なのですが、ここには多くの根拠が隠されています。
まず、なぜ、
3x-5=4
3x=9
となるのでしょうか?
「移項したから」
と答えられる子は、移項という数学用語を使えるだけ賢い子ではあるのですが、ではなぜ移項は可能なのか?
なぜ、左辺の-5は、右辺に移項されると+5になるのか?
そこを説明できるか、できないかが、大きな分岐点です。
「移項するときは符号を変える」
というやり方だけ覚えているのか、それとも、意味がわかっているのか?
3x-5 =4
両辺に5を加えて、
3x-5+5=4+5
3x=9
いちいち書き記さないだけで、実際は、このような作業が行われています。
使われているのは、上の等式の性質のうち、
ア. A=Bのとき、A+C=B+C
です。
等式は、左辺と右辺が等しいという関係を表した式。
左辺と右辺に、それぞれ同じものを加えても、等しい関係は変わらないのです。
その性質を利用して、両辺に5を加えると、-5+5=0となります。
方程式を解くのに邪魔だった左辺の-5を消すことができるのです。
続けて、
3x=9
両辺を3で割って、
x=3
ここで使われている等式の性質は、
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
です。
左辺と右辺を同じもので割っても、等しい関係は変わらない。
その性質を利用しています。
しかし、このような解説を、恐ろしいくらいに理解できない子たちもいます。
それは学力が低いためとは限らないのです。
方程式の解き方自体はスラスラと身につけます。
かなり複雑な、( )を含んでいたり、係数が分数な方程式も。
ところが、上のような根拠を問う問題になると、凝固したようになり、全く話が通じなくなります。
「聞いてますか?」
「わかりますか?」
「どこがわからないですか?」
と繰り返し問いかけても、全く反応がなく、呆然としてしまうのです。
何がわからないのかを説明することもできず、ただ黙り込む。
だから、こちらとしては推測するしかないのですが、考えられることは、上のように、方程式の解き方の根拠を問う問題は、その子の考える「算数・数学の問題」の概念から大きく外れているのではないか?
彼らにとって、そうした問題は、宇宙人の話す宇宙語よりも異様であり、理解の範疇を超えている。
何を問われているのか、全く意味がわからない。
彼らにとっては、やり方を覚えることが算数・数学の学習であり、根拠を問う問題など、算数・数学の問題ではないのでしょう。
その間違った固定観念を打破しないと、上のような問題を理解することができないままかもしれません。
正攻法の説明を繰り返しても全く話が通じないときに、最後の手段を講じることがあります。
「この問題は、テストに出ます。
中学の定期テストはそういうもの。
小学校の算数とは違います」
テストに出るぞ。
テストに出るぞ。
テストに出るぞ。
どう考えても、教育的ではありません。
しっかりと意味を伝えることをまず優先するべきです。
しかし、相手の固定観念があまりにも強く、このままでは膠着状態が続く。
テストが近づいている。
そうしたときに、この最後の手段を講じます。
テストに出るぞ。
このあまりにも打算的な言葉が、意味が通じず凝固していた子には響くことがあるのです。
「やり方だけ覚えればいい」という考え方と、「テストに出るぞ」という考え方は親和性が高いからでしょう。
明らかに表情が変わります。
彼らは、計算のやり方の根拠を問う問題などテストに出るわけがないという、これも間違った固定観念に凝り固まり、そのせいで理解する気がそもそもなかったのかもしれません。
しかし、これがテストに出るのなら、このタイプの問題の「解き方」も覚えなければならないのです。
でも、こういう問題の解き方って・・・?
それは、結局、計算のやり方の意味を理解することになるのです。
正攻法では不可能だった、根拠を考える学習が、この形で可能になることがあります。
もう一度、上の問題を。
問題
3x-5=4・・・①
3x=9 ・・・②
x=3 ・・・③
上の①から②の間、②から③の間に使われた等式の性質を以下のア~エから選び、記号で答えなさい。
ア. A=Bのとき、A+C=B+C
イ. A=Bのとき、A-C=B-C
ウ. A=Bのとき、AC=BC
エ. A=Bのとき、A / C=B / C (ただしC ≠ 0)
「①から②の間に、等式の性質のどれを利用しているんでしょう?」
「・・・イ?」
「あー・・・、-5を消したのだから、ひき算だと思った?
いや、そうじゃないんですよ。
3x-5+5=4+5
というふうに計算しているんです。だから?」
「・・・エ?」
「・・・何で?」
このような会話を交わすことも多いです。
方程式を解くだけならできる子が、こんなにも理解していないのだと、こうした会話を通してわかります。
その子の中の数学に関する底知れない深淵が垣間見えるようです。
その深淵は、その子が、小学校の6年間で作ってきた深淵。
下手をすると、深淵が広がり、乗っている板1枚の下には何もない状態になってしまいます。
実際、高校数学を学習していて、そのような状態の子もいます。
深淵は知識で埋めていく作業が必要です。
やり方だけ覚えてやり過ごしてきたためにできてしまった深淵は、こんな1問だけで埋まるわけではありませんが、一助にはなります。
学年が上がれば、太郎さんと花子さんが、問題の解き方について、べらべらと1ページ以上も会話する問題も定期テストに出ます。
言うまでもなく、大学入試共通テスト型の問題です。
それは、学校によっては、中学の定期テストから始まります。
意味がわからなければ、太郎さんと花子さんの会話の空欄は埋まりません。
2024年07月04日
「三か月でマスターする数学」は興味深い番組です。
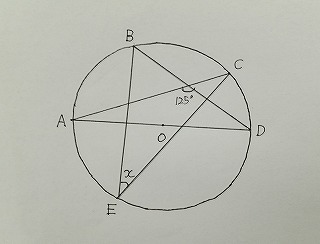
問題 上の図の x の角の大きさを求めよ。
NHK Eテレで「三か月でマスターする数学」という番組が7月から始まりました。
この種の数学番組は、大学数学を扱うことが多いのですが、この番組は、中3の数学から始まりました。
第1回は「円周角の定理」。
数学が苦手な女性アナウンサーに、講師が数学を教えるという形で番組は進行します。
この設定がまず興味深いです。
数学が苦手な子は、数学に対して寡黙です。
「何がわからない?」
と尋ねても、返答がないことがあります。
私が板書を指さしながら、
「この行はわかる?ここは?」
と1行1行確認しようとしても、パニックを起こしているのか、私のそうした意図を察してくれず返答がないことすらあります。
気持ちを落ち着かせ、私の意図を理解してもらい、1行1行、どこがわからないのかを確認していく。
それが私の仕事です。
数学は苦手なのだが、コメント力のある生徒。
これは、数学を教える者から見ると、理想の生徒です。
何がわからないから、数学がわからないのか。
私が知りたいのは、まさにそれです。
しかし、番組は私の予想外の方向に進んでいきました。
番組前半、基本の解説が行われました。
等しい弧の円周角は等しい。
特に、半円の弧の円周角は90度である。
そして、練習問題を解くことになりました。
それが、上の問題です。
数学が苦手なアナウンサーは、やはり、解くことができません。
そこで、講師からヒントが出されました。
「補助線を引いてみましょう」
上の図に戻ってください。
この問題、補助線を1本入れれば、かなりわかりやすくなります。
どこに補助線を入れたらいいでしょうか?
ここで、アナウンサーが入れた補助線は、線分BCでした。
私は天を仰ぎました。
そうだ。
そうなんですよ。
図形が苦手な人は、そうなんですよね。
いや、この番組は、台本があってのことで、そのアナウンサーは狂言回しで、わざとやっているのかもしれませんが、怖いくらいの既視感でした。
そのとき、しかし、講師の人は、こちらのほうがいいですよと、さっさとABに補助線を入れました。
講師の助言を受け、上手く誘導されて、アナウンサーは、そのままやがて正解にたどりつき、満足そうでした。
台本ではなく、本気で満足しているようだと感じるほどに。
そこで、私は再度天を仰いでしまったのでした。
この番組は、大人が数学を少し楽しむ番組だから、それでいいのです。
中学の数学は、今やり直せば案外いけるかも、と思う気持ちが大切。
数学に抵抗感がなくなることが大切。
番組の趣旨はそうなのですが、私の仕事はそうではありません。
生徒に数学のテストで良い点を取ってもらうこと。
目標は、その一点に絞られています。
数学が好きになって、それで得点も上がるなら、それは何より。
ただ、数学は特に好きにはならなくても、得点が上がるのならば、それでもいいのです。
人は、自分が上手くできることには好感を抱くものなので、得点が上がれば今までほどの嫌悪感はなくなります。
得点が上がるのが先でも構わないのです。
つまりは、自力で問題に正解できることが大切。
そして、その観点でこの番組を見ると、感じるのです。
このアナウンサーは、わかったつもりにはなっているが、類題を自力で解くことはできないでしょう。
なぜか?
有効な補助線を入れることが自力でできないからです。
類題ではまた、問題を解く最初の一歩でつまずくでしょう。
そして、図形問題が苦手な人の多くが、そうなのです。
もう一度、上の図に戻ってください。
アナウンサーは、線分BCを補助線として入れたのです。
・・・何で、そこに補助線を入れるかなあ?
でも、図形が苦手な子は、確かに、線分BCのような、あまり役に立たない補助線を入れることが多いのです。
予想外のところに補助線を入れます。
何でなのかなあ?
図形の問題が自力で解けないというのは、結局、そこなのです。
BCに補助線を入れていては、この問題は解けないのです。
そして、番組の講師は、補助線はなぜBCではなくABなのかについては解説せず、そこはさっと通り過ぎて、アナウンサーが自力で解いているかのような雰囲気を作っていました。
正しい補助線を自力で入れられない限り、テストで類題は解けないのですが。
学校や塾の集団授業はしっかり聞いているのに、数学の成績が上がらない・・・。
評判のいい数学動画を見て、理解した気がするのに、数学の成績が上がらない・・・。
その理由をあえて描いているような番組でした。
私は、図形に特別な才能を持っているわけではないので、上のような問題を見たときに、一瞬で最後まで解法を見通すことはできません。
先は見えないまま、とりあえず補助線を入れてみるのが常です。
番組を見ていたときも、そうでした。
補助線は線分ABだなあとテレビ画面を見ながらぼんやり思っていました。
それは、勘です。
長年、この種の問題は沢山解いていますから、経験の多さから勘が働きます。
しかし、勘ではダメです。
生徒に教えるならば、そこを理論化しなければなりません。
補助線はどう入れるのか。
補助線の入れ方の原則。
①結ばれていない点と点とを結ぶ。
②既に存在する線分を延長させる。
③既に存在する線分と平行な線を引く。
④既に存在する線分に垂線を下ろす。
勘で解けないのならば、理屈で解く。
そうはいっても、結ばれていない点と点とを結ぶのならば、線分BCも、そうなのです。
なぜ、線分BCを真っ先に思いついてしまうのか。
数学が苦手だけれどコメント力のあるアナウンサーには、そこを語ってほしかった。
なぜBCに補助線を入れたのか。
どういう考えでそうしてしまうのか。
私が知りたいのは、そこなのです。
線分BCを書き込んで、△BCEを作っても、それでは図は動きません。
それが x の角に一番関係があると思って書き込んでしまうのでしょうか。
そこに対して自覚的になれば、自分の思考の癖に気づくことができます。
それが改善への道です。
シンプルに、x の角を円周角の定理でどこかに移したいな、という発想だけでも、補助線はABが有力です。
さらに言えば、直前に、半円の弧の円周角は90度と学習したばかりなのだから、どうせ作るならば直角三角形を作りましょう。
円周角の問題は、直角三角形が作れるのならば、作る。
図中に円の直径が描かれているのならば、必ず直角三角形が作れます。
それが鉄則。
しかし、そう指示すると、今度は、頂点Bから直径ADに垂線を下ろす、という荒業を繰り広げる子もいます。
円周角を学習したのだから、それを活かすことを考えよう。
半円の弧の円周角は90度であることを、どこかで使えないか。
そういう発想で問題に向かえば、有効な補助線を引けるはずなのですが、図形が苦手な子は、学習したことを、それはそれとして、問題を解くときにはポンと脇に置いてしまいます。
学んだことを使って問題を解くという発想がない。
そこが脳の中で繋がっていないように感じます。
わかったつもりになっただけでは、実際の問題は解けません。
自分で解いて、間違えて。
正解を知って、そこから重要なことを吸収して。
その繰り返しで、図形問題への「勘」「センス」は養われます。
生徒たちの「予想外の補助線」と格闘し、何でそんなところに補助線を入れたいのか、その傾向を分析し、そこへの経路を塞ぎ、何とか類題でも正解できるように経験値を高めていく。
それが私の仕事です。
最後に、上の問題の解答を。
上の図を書き写して、補助線ABを入れてください。
弧BCに対する円周角は等しいから、∠BEC=∠BAC。
すなわち、∠BAC=x です。
また、線分ADはこの円の直径ですから、∠ABDは、半円の弧の円周角。
すなわち、∠ABD=90°
ここで、△ABDだけに目を奪われないことがコツです。
ここも、生徒が苦手とするところです。
着目する三角形が頭の中で固定され、そこから離脱できないことがありますが、乗り換えていくのが図形問題の常。
ACとBDの交点、125°のところの点を点Fとし、新しく△ABFに着目します。
∠BAF=x
∠ABF=90°
そして、∠AFBは、125°のところの外角ですから、
180-125=55 で、
∠AFB=55°
三角形の内角の和は180°ですから、求める角xは、
180-90-55=35
x=35 です。
NHK Eテレで「三か月でマスターする数学」という番組が7月から始まりました。
この種の数学番組は、大学数学を扱うことが多いのですが、この番組は、中3の数学から始まりました。
第1回は「円周角の定理」。
数学が苦手な女性アナウンサーに、講師が数学を教えるという形で番組は進行します。
この設定がまず興味深いです。
数学が苦手な子は、数学に対して寡黙です。
「何がわからない?」
と尋ねても、返答がないことがあります。
私が板書を指さしながら、
「この行はわかる?ここは?」
と1行1行確認しようとしても、パニックを起こしているのか、私のそうした意図を察してくれず返答がないことすらあります。
気持ちを落ち着かせ、私の意図を理解してもらい、1行1行、どこがわからないのかを確認していく。
それが私の仕事です。
数学は苦手なのだが、コメント力のある生徒。
これは、数学を教える者から見ると、理想の生徒です。
何がわからないから、数学がわからないのか。
私が知りたいのは、まさにそれです。
しかし、番組は私の予想外の方向に進んでいきました。
番組前半、基本の解説が行われました。
等しい弧の円周角は等しい。
特に、半円の弧の円周角は90度である。
そして、練習問題を解くことになりました。
それが、上の問題です。
数学が苦手なアナウンサーは、やはり、解くことができません。
そこで、講師からヒントが出されました。
「補助線を引いてみましょう」
上の図に戻ってください。
この問題、補助線を1本入れれば、かなりわかりやすくなります。
どこに補助線を入れたらいいでしょうか?
ここで、アナウンサーが入れた補助線は、線分BCでした。
私は天を仰ぎました。
そうだ。
そうなんですよ。
図形が苦手な人は、そうなんですよね。
いや、この番組は、台本があってのことで、そのアナウンサーは狂言回しで、わざとやっているのかもしれませんが、怖いくらいの既視感でした。
そのとき、しかし、講師の人は、こちらのほうがいいですよと、さっさとABに補助線を入れました。
講師の助言を受け、上手く誘導されて、アナウンサーは、そのままやがて正解にたどりつき、満足そうでした。
台本ではなく、本気で満足しているようだと感じるほどに。
そこで、私は再度天を仰いでしまったのでした。
この番組は、大人が数学を少し楽しむ番組だから、それでいいのです。
中学の数学は、今やり直せば案外いけるかも、と思う気持ちが大切。
数学に抵抗感がなくなることが大切。
番組の趣旨はそうなのですが、私の仕事はそうではありません。
生徒に数学のテストで良い点を取ってもらうこと。
目標は、その一点に絞られています。
数学が好きになって、それで得点も上がるなら、それは何より。
ただ、数学は特に好きにはならなくても、得点が上がるのならば、それでもいいのです。
人は、自分が上手くできることには好感を抱くものなので、得点が上がれば今までほどの嫌悪感はなくなります。
得点が上がるのが先でも構わないのです。
つまりは、自力で問題に正解できることが大切。
そして、その観点でこの番組を見ると、感じるのです。
このアナウンサーは、わかったつもりにはなっているが、類題を自力で解くことはできないでしょう。
なぜか?
有効な補助線を入れることが自力でできないからです。
類題ではまた、問題を解く最初の一歩でつまずくでしょう。
そして、図形問題が苦手な人の多くが、そうなのです。
もう一度、上の図に戻ってください。
アナウンサーは、線分BCを補助線として入れたのです。
・・・何で、そこに補助線を入れるかなあ?
でも、図形が苦手な子は、確かに、線分BCのような、あまり役に立たない補助線を入れることが多いのです。
予想外のところに補助線を入れます。
何でなのかなあ?
図形の問題が自力で解けないというのは、結局、そこなのです。
BCに補助線を入れていては、この問題は解けないのです。
そして、番組の講師は、補助線はなぜBCではなくABなのかについては解説せず、そこはさっと通り過ぎて、アナウンサーが自力で解いているかのような雰囲気を作っていました。
正しい補助線を自力で入れられない限り、テストで類題は解けないのですが。
学校や塾の集団授業はしっかり聞いているのに、数学の成績が上がらない・・・。
評判のいい数学動画を見て、理解した気がするのに、数学の成績が上がらない・・・。
その理由をあえて描いているような番組でした。
私は、図形に特別な才能を持っているわけではないので、上のような問題を見たときに、一瞬で最後まで解法を見通すことはできません。
先は見えないまま、とりあえず補助線を入れてみるのが常です。
番組を見ていたときも、そうでした。
補助線は線分ABだなあとテレビ画面を見ながらぼんやり思っていました。
それは、勘です。
長年、この種の問題は沢山解いていますから、経験の多さから勘が働きます。
しかし、勘ではダメです。
生徒に教えるならば、そこを理論化しなければなりません。
補助線はどう入れるのか。
補助線の入れ方の原則。
①結ばれていない点と点とを結ぶ。
②既に存在する線分を延長させる。
③既に存在する線分と平行な線を引く。
④既に存在する線分に垂線を下ろす。
勘で解けないのならば、理屈で解く。
そうはいっても、結ばれていない点と点とを結ぶのならば、線分BCも、そうなのです。
なぜ、線分BCを真っ先に思いついてしまうのか。
数学が苦手だけれどコメント力のあるアナウンサーには、そこを語ってほしかった。
なぜBCに補助線を入れたのか。
どういう考えでそうしてしまうのか。
私が知りたいのは、そこなのです。
線分BCを書き込んで、△BCEを作っても、それでは図は動きません。
それが x の角に一番関係があると思って書き込んでしまうのでしょうか。
そこに対して自覚的になれば、自分の思考の癖に気づくことができます。
それが改善への道です。
シンプルに、x の角を円周角の定理でどこかに移したいな、という発想だけでも、補助線はABが有力です。
さらに言えば、直前に、半円の弧の円周角は90度と学習したばかりなのだから、どうせ作るならば直角三角形を作りましょう。
円周角の問題は、直角三角形が作れるのならば、作る。
図中に円の直径が描かれているのならば、必ず直角三角形が作れます。
それが鉄則。
しかし、そう指示すると、今度は、頂点Bから直径ADに垂線を下ろす、という荒業を繰り広げる子もいます。
円周角を学習したのだから、それを活かすことを考えよう。
半円の弧の円周角は90度であることを、どこかで使えないか。
そういう発想で問題に向かえば、有効な補助線を引けるはずなのですが、図形が苦手な子は、学習したことを、それはそれとして、問題を解くときにはポンと脇に置いてしまいます。
学んだことを使って問題を解くという発想がない。
そこが脳の中で繋がっていないように感じます。
わかったつもりになっただけでは、実際の問題は解けません。
自分で解いて、間違えて。
正解を知って、そこから重要なことを吸収して。
その繰り返しで、図形問題への「勘」「センス」は養われます。
生徒たちの「予想外の補助線」と格闘し、何でそんなところに補助線を入れたいのか、その傾向を分析し、そこへの経路を塞ぎ、何とか類題でも正解できるように経験値を高めていく。
それが私の仕事です。
最後に、上の問題の解答を。
上の図を書き写して、補助線ABを入れてください。
弧BCに対する円周角は等しいから、∠BEC=∠BAC。
すなわち、∠BAC=x です。
また、線分ADはこの円の直径ですから、∠ABDは、半円の弧の円周角。
すなわち、∠ABD=90°
ここで、△ABDだけに目を奪われないことがコツです。
ここも、生徒が苦手とするところです。
着目する三角形が頭の中で固定され、そこから離脱できないことがありますが、乗り換えていくのが図形問題の常。
ACとBDの交点、125°のところの点を点Fとし、新しく△ABFに着目します。
∠BAF=x
∠ABF=90°
そして、∠AFBは、125°のところの外角ですから、
180-125=55 で、
∠AFB=55°
三角形の内角の和は180°ですから、求める角xは、
180-90-55=35
x=35 です。
Posted by セギ at
12:47
│Comments(0)






















