2017年11月30日
三角比と測量の問題。図だけで問題を解くのはむしろ難しいです。
今回も、「三角比」の学習。
測量への利用です。

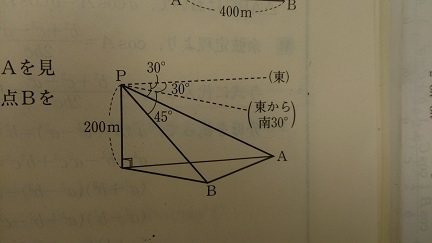
問題 図のように、高さ200mの山頂Pから東方にある地点Aを見たら、俯角が30°であった。また、東から南30°にある地点Bを見たら、俯角が45°であった。
2地点A、B間の距離を求めよ。
この問題は、まず問題の意味を理解できるかどうかが1つ目のハードルです。
2地点A、B間の距離を求めよ。
この問題は、まず問題の意味を理解できるかどうかが1つ目のハードルです。
こうやってネットに書いた場合、図の画像の粗さとネットの文字の読みにくさと、どちらがより強く影響するかという問題もあると思います。
しかし、これをテキストで見た場合、図を先に見るか活字を先に見るかは、その人の普段の傾向がそのまま表れるのではないでしょうか。
図の情報を優先する人と、文字情報を優先する人と。
高校生の中には、図しか見ない子がいます。
それではこの問題は解けないでしょう。
図の上のほうの点線と、それぞれの示す角度が何を意味しているのか、図だけではわからないです。
むしろ、問題文だけのほうがまだ情報を整理しやすいかもしれません。
ただ、それにはある程度の読解力が必要なのも事実です。
文字情報を頭の中で具体的なイメージにすることができないと、問題文だけでは理解しづらいと思います。
つまりは「ちゃんと両方見なさいよ」という当たり前の話なのですが、それができない高校生は意外に多いのです。
ここで言う読解力・イメージ力とは、上の問題文を読んだとき、イメージとして自分が山頂Pに立てるかどうか、です。
図を見る場合でも、自分がスモールライトを浴びて山頂Pに立つと、問題の構造が理解しやすくなると思いす。
これは中学3年生に理科の「天体」の授業をしているときもそう感じることです。
月の見え方や金星の見え方に関する問題は、図の中の地球に自分が立って月や金星がどう見えるかをイメージできれば易しいです。
しかし、それができず、外から地球を眺めているままですと、何でそう見えるのかうまく理解できません。
さあ、イメージします。
山頂Pに立ってみましょう。
標高200m。里の低山でしょうか。
埼玉県飯能の天覧山が標高197m。
寄居の羅漢山が標高247m。
毎日のお散歩コースにこのくらいの山があったらいいなあ。
それはともかく。
この山は、南面の見晴らしが良いようです。
だから、南を向いて立っています。
すると、東の方向俯角30°にA地点が見えました。
俯角というのは、水平から下に30°の角度で見えたということです。
ここで目を転じ、水平に30°南方向に目を向けると、今度は俯角45°にB地点が見えました。
さて、AB間の距離は?
という問題なのですね。
ここで、山頂PとAとBを結んで、△PABで解こうとしてしまうと間違えます。
∠APB=30° と誤解しそうですが、そうではないからなんです。
AとBの間が30°なのは水平での話で、斜めになると角度は変わります。
山頂Pの真下、標高0mの地点をHとしましょう。
△HABに着目すると、AB間の距離を求めることができます。
∠AHB=30° です。
AHの長さは?
これは△PHAに着目します。
30°、60°、90°の直角三角形ですね。
PHが200mなので、AHは200√3mです。
次に、BHの長さは?
これは△PHBに着目しましょう。
45°、45°、90°の直角三角形です。
PHが200mなので、BHも200mです。
これで、△HABにおいて2辺とその間の角がわかりました。
これならABの長さは計算で求められますね。
余弦定理より、
AB2=AH2+BH2-2・AH・BH・cos∠AHB
=(200√3)2+2002-2・200√3・200・√3/2
=40000・3+40000-40000・3
=40000
AB>0より
AB=200
よって答えは200mとなります。
2017年11月28日
上川乗から笹尾根を歩いてきました。2017年11月。
2017年11月26日(日)、笹尾根を歩いてきました。
ホリデー快速あきかわ3号に乗って、終点武蔵五日市駅下車。
2週間前も同じ電車に乗りましたが、乗客が随分減っています。
楽に座っていくことができました。
紅葉シーズンも終わり、これから、山は静かになっていきます。
駅前から、数馬行きのバスに乗車。9:00。
2台で発車。
上川乗バス停下車。9:40。
降りたのは、私1人。
これは観光シーズンでもそうなので、あまり気になりません。
バスの進行方向に少し歩き、三叉路でバスと別れて左折します。
大きな橋で秋川を渡り、そのまま、道なりに舗装道路を登っていきます。
ほどなく、左手に上川乗登山口。9:50。
道しるべはありますが、登山口は狭く、最初に歩いたときは心細かったなあと思い出しながら、歩いていきました。
夏草が邪魔しないので、細い山道も意外に歩きやすく、楽に尾根に乗ることができました。
紅葉はもうほとんど終わっていますが、たまに朝の日差しに明るく輝く木があります。
上の画像がそれです。
尾根に乗った少し先、登山道は尾根から一段下がった道が続きます。
やがて、尾根を乗り越えて、そのすぐ先が、浅間峠。11:00。
あずまやとベンチがあります。
ここから笹尾根に合流です。
まずは上り坂。
風があり、落ち葉が舞っていました。
斜面は落ち葉がとどまらず常に動いているので、登山道もそれ以外のところも同じように見えてしまいます。
足元の固さをよく確認しながら先に進みました。
アップダウンを繰り返し、日原峠。11:50。
古道らしい小さな石像があり、手を合わせました。
落ち葉かさらに深くなり、尾根が広いところは登山道がわかりません。
地形を考えて、尾根から外れないように注意しながら先に進みました。
熊鈴の音。
カサカサと落ち葉を踏む音。
人のいない、晩秋の山道です。
登っていくと、土俵岳。12:10。
御前山と大岳山がよく見えました。
景色を眺めながら、汗を拭きました。
追い付いてきた人。
向こうから来る人。
この道を今日歩くのは自分だけではないとわかり、ほっとしました。
南側の樹間から富士山が見えます。
笹尾根は、これまでよく夏に歩いていました。
歩く途中にも、富士山は見えるんだなあ。
先程追い越していった人が、樹木が切れて富士山のよく見える場所で休憩していました。
日向が気持ちよさそうです。
丸山が見えてきました。
名前の通り、こんもりとなだらかに丸い山です。
単なる笹尾根の途中の山としては予想外に大きい円かな山。
ゆっくりと登っていきます。
山頂まであと少し。
でも、山頂に何もないのは知っているから、まき道をいこう。
笛吹峠。13:15。
ここだけ尾根が広くなり、丸太がいくつか並べてあります。
その1つに座って休憩。
ここは見晴らしはないですが、晩秋の林の様子を眺めながらのお昼にします。
今日は大洗町漁業協同組合協力の、しらすおにぎりセットをコンビニで購入しました。
封を開くと、3種類のしらすおにぎりが入っています。
おいしい。
おかずが漬物だけなのは、少し寂しいかな。
おにぎり2つで、少しおかずがついているといいなあ。
熱いカフェオレを飲んで、チョコレートを食べて。
ちょっとのんびりしすぎました。
さて、出発。
道が尾根道とまき道の二又に別れるところでは、尾根道にトレイルランニング大会用の赤い矢印がつけられていました。
12月2日(土)に開かれる大会です。
南高尾山稜から、関東ふれあいの道を通って、笹尾根を数馬まで行く全長42km。
もう準備が進んでいるんだなあ。
数馬峠に到着。14:00。
南面の見晴らしの良い峠です。
富士山の青い姿がくっきりと見え、前景はススキが揺れています。
しっかりしたベンチもあり、休憩はここでも良かったかもしれません。
ここから登山道は尾根と離れ、斜面のまき道になります。
道が細く、ところどころ崩壊していたり、霜が降りていたり。
用心して歩いていくと、西原峠。14:35。
そこから5分登って、槇寄山。
本日の最高点です。
晴れ晴れとした山頂です。
ここにもベンチがあり、富士山が見えました。
三頭山までは急登をあと2時間。
時間的にもう無理ですね。
西原峠に戻って、そこから、道しるべに従い、仲の平バス停へと下りました。
夏の頃は、道が泥んこで踏ん張りがきかないところが少しある、林の中の道です。
晩秋の今は、霜柱が午後になっても融けずに残っていました。
そして、枯葉の堆積。
枯葉の下に段差や石が隠れていることがあるので、歩きにくい下り道でした。
トレッキングポールでさぐりながら歩を進めます。
ときおり、鮮やかな紅葉に出会います。
この時間の光では、写真に撮ってもきれいに写らないでしょう。
スマホは出さず、ただ見上げ、眺めて楽しむ。
それも贅沢な気がします。
急な山道からあっけなく農地に出て、さらに下っていくと、舗装路に。
そこからは、とにかく下りの道を選んでいくと、檜原街道に出ます。
街道の手前で、大会の赤い矢印を設置している人と遭遇。
土俵岳で追い抜いていった人です。
今日1日、山の中で矢印の設置作業をされていたのですね。
長い42kmを分担して、この作業をされていた方が各地にいるのでしょう。
ご苦労さまです。
さて、温泉センター数馬の湯。16:00。
温泉に入っていくつもりで、お風呂セットも持ってきたのですが、16:08のバスに乗ると、17:21のホリデー快速に間に合って、三鷹に早く帰れるなあ。
その誘惑に勝てず、今日は温泉はパスしました。
バス停の行列も、2週間前と比べると半減しています。
バスは2台。
座っていくことができました。
檜原街道を駅へと向かうバスの車窓からも、夕陽の中で赤く輝く紅葉をたくさん見ることができました。
2017年11月24日
三角比と余弦定理。上手な利用の仕方。
「三角比」の学習。いよいよ佳境です。
今回は、余弦定理の学習をしましょう。
△ABCにおいて、
a2=b2+c2-2bc cosA
b2=c2+a2-2ca cosB
c2=a2+b2-2ab cosC
公式としては、きちんとサイクリックで覚えておいたほうが良いです。
今回は、余弦定理の学習をしましょう。
△ABCにおいて、
a2=b2+c2-2bc cosA
b2=c2+a2-2ca cosB
c2=a2+b2-2ab cosC
公式としては、きちんとサイクリックで覚えておいたほうが良いです。
サイクリックとは、ab、bc、ca、といった循環のことです。
caを見ると、必ず「ac」と直そうとする人が、数学が苦手な人の中にときどきいるのですが、それは不要なこと。
a、b、cしか文字がない式の場合、caのほうがサイクリックで美しいのです。
そして、普段からそのような意識を持って文字を見ていれば、余弦定理は、3本あるように見えて、実は1本の公式であることが理解できると思います。
文字を順番に使っているだけなのがわかりますね。
余弦定理の証明はここでは省略しますが、使うのは、三角比と三平方の定理です。
そう難しいものではないですので、興味があれば、検索してみてください。
課題は、やはり余弦定理をどう利用するか、です。
問題 △ABCにおいて、b=1、c=√2、A=45°のとき、aを求めよ。
a2=b2+c2-2bc cosA
に代入すれば良いですね。
というわけで、答案としては、
余弦定理より
a2=1+2-2・1・√2・1/√2
=1+2-2
=1
a>0 より
a=1
問題 △ABCにおいて、a=√2、b=2、c=√3-1のとき、Bを求めよ。
角の大きさを求める場合、余弦定理を変形させた式を覚えておくと楽です。
それも含めて余弦定理です。
今回利用するのは、
cosB=(c2+a2-b2)/2ca
という式です。
b2=c2+a2-2ca cosB
を、cosBについて解いた式ですね。
余弦定理より
cosB={(√3-1)2+2-4}/2・(√3-1)・√2
=(3-2√3+1+2-4)/2√2(√3-1)
=(2-2√3)/(2√6-2√2)
=(1-√3)/(√6-√2)
=(1-√3)(√6+√2)/(6-2)
=(√6+√2-3√2-√6)/4
=-2√2/4
=-√2/2
0°<B<180°より
B=135°
これは、一番地道な解き方で解きました。
しかし、この計算過程を正しくたどれない高校生は多いです。
複雑な式の中で、2乗の乗法公式を忘れてしまう人。
分母が2種類のルートのとき、どうやって有理化するのかわからない人。
単純な符号ミスを起こしやすい人。
複雑な計算をしているとストレスが強くかかるのか、数字の書き間違いをしてしまう人。
エラーの原因は無数に存在します。
一方、数学が得意な人は、答えをある程度予想し、それにそって式を変形します。
上の問題は、「Bを求めよ」と言われています。
Bは角度です。
cosBを求めよと言われているわけではありません。
三角比の表を使わない限り、三角形の角度は、30°、45°、60°、90°、120°、135°、150°のどれかでなければ計算では求められません。
15°や75°などの特殊な角度の三角比を暗記している人もいますが、その暗記を前提とした問題が出題されることはまずありません。
ということは、角度を求める問題ならば、コサインの値は、見慣れた数字のどれかになるものです。
それを見越してまとめていくと、計算はかなり楽になります。
cosB={(√3-1)2+2-4}/2・(√3-1)・√2
=(3-2√3+1+2-4)/2√2(√3-1)
=(-2√3+2)/2√2(√3-1)
=-2(√3-1)/2√2(√3-1)
ここで、分母・分子を(√3-1)で約分して、
=-2/2√2
=-1/√2
分母の√3-1 は、三角比としては必要のない数字です。
これは、おそらく約分できるでしょう。
だから、最初から( )を開かないのです。
その方向で分子をまとめていくと、確かに、同じ√3-1の要素が出てきます。
そういうまとめ方です。
地道な解き方でも良いのですが、地道な解き方ほど煩雑な計算に耐えられる計算力が必要です。
しかも、地道に計算すると答えは-√2/2となります。
これが-1/√2 と等しいことがわからず、B=135°と求められない人もいます。
いろいろなことが悲しい結果に終わりがちなのが、余弦定理です。
( 一一)
ところで、cosB= などで始まる余弦定理について、数学が得意な人は、
「こんな式、覚えていなくても、必要になったらいつでも復元できる」
と簡単に言うのですが、四則計算に今ひとつ習熟しきれていない高校生の場合、普通の余弦定理をこの形にすぐに変形できるかというと、残念ながらできない場合があります。
式の変形はなぜそれほどハードルが高いのでしょうか。
方程式なら計算できるのに。
例えば、
3x=2
を解けない高校生はほとんどいないと思います。
数字とxだけの方程式なら解くことができるのです。
けれど、それは解き方を覚えているだけで、等式の原則を理解して操作しているわけではないのかもしれません。
だから、極端な話、
2=3x
という見た目になっただけで、もう計算できなくなる子もいます。
手順を暗記しているだけの人の計算力は脆弱で、少しの揺さぶりに耐えられないのです。
cosB= の形の式を別に暗記しておくのが安全でしょう。
同時に、中学の数学に戻って、「式の変形」を復習すると良いと思います。
苦手だから、嫌いだからと言って、避けていなかったでしょうか。
式の変形の仕方さえ理解できていれば、確かに、cosB= の公式なんてすぐに復元できるのです。
ところで、もっと応用問題になって、複雑な図形の中で余弦定理を利用する場合に、aにあたる長さを求めるのに、どちらがbでどちらがcにあたるかわからなくて、混乱してしまう人がいます。
実は、そんなことは、考える必要がないのです。
bとcなんて、どっちがどっちだっていいのです。
余弦定理は、3本も式があることもあって、初めて見ると動揺しがちなのですが、これは、三角形の合同条件と連動して考えれば、とてもシンプルな式です。
一番上のa2から始まる式を例にとって考えてみると、Aというのはその対角、bとcは残る2辺であることがわかります。
すなわち、右辺にあるのは、「2辺とその間の角」なのです。
つまり、余弦定理は、2辺とのその間の角がわかれば、残る1辺の長さは計算できる、という定理です。
bとcが逆転しても、計算の結果には全く影響しません。
どうせ、図を裏返せば、bとcはひっくり返るのですから。
とにかく、2辺とその間の角から残る1辺の長さを計算できるのです。
そういうことが把握できると、余弦定理はざっくりと、そして快適に利用できるようになります。
bとcなんて、どっちがどっちだっていいのです。
余弦定理は、3本も式があることもあって、初めて見ると動揺しがちなのですが、これは、三角形の合同条件と連動して考えれば、とてもシンプルな式です。
一番上のa2から始まる式を例にとって考えてみると、Aというのはその対角、bとcは残る2辺であることがわかります。
すなわち、右辺にあるのは、「2辺とその間の角」なのです。
つまり、余弦定理は、2辺とのその間の角がわかれば、残る1辺の長さは計算できる、という定理です。
bとcが逆転しても、計算の結果には全く影響しません。
どうせ、図を裏返せば、bとcはひっくり返るのですから。
とにかく、2辺とその間の角から残る1辺の長さを計算できるのです。
そういうことが把握できると、余弦定理はざっくりと、そして快適に利用できるようになります。
2017年11月22日
三角比と正弦定理。
「三角比」の学習も佳境。
今回は、「正弦定理」を学習しましょう。
⊿ABCにおいて、
a/sinA=b/sinB=c/sinC=2R
(ただし、Rは三角形の外接円の半径)
今回は、「正弦定理」を学習しましょう。
⊿ABCにおいて、
a/sinA=b/sinB=c/sinC=2R
(ただし、Rは三角形の外接円の半径)
∠Aの対辺がa、∠Bの対辺がb、∠Cの対辺がcです。
これが正弦定理です。
高校数学の定理としては比較的簡単に証明できるものです。
これが正弦定理です。
高校数学の定理としては比較的簡単に証明できるものです。
図が必要なので、ここでは説明しませんが、検索すればすぐに証明は出てくると思います。
鋭角三角形、直角三角形、鈍角三角形に場合分けして証明しなければならないのが多少わずらしいでしょうか。
証明の根拠は、中学三年生で学んだ「円周角の定理」です。
鋭角三角形、直角三角形、鈍角三角形に場合分けして証明しなければならないのが多少わずらしいでしょうか。
証明の根拠は、中学三年生で学んだ「円周角の定理」です。
証明を理解し、納得したら、あとは定理の利用。
こちらのほうが重要です。
正弦定理が凄いのは、三角形の合同条件と連動していることです。
三角形の合同条件の1つに、「1組の辺とその両端の角がそれぞれ等しい」というものがあります。
その条件を満たす三角形は合同だということ。
すなわち、そのような三角形は、この世に1つしかないということです。
この世に1つしかない三角形ならば、残る1つの角の大きさと2つの辺の長さは定まっているでしょう。
それを計算できるのが、正弦定理です。
残る1つの角は、三角形の内角の和が180°であることから、楽々と計算できます。
あとは、正弦定理を用いれば、残る2辺の長さは簡単に出てきます。
ヽ(^。^)ノ
正弦定理が凄いのは、三角形の合同条件と連動していることです。
三角形の合同条件の1つに、「1組の辺とその両端の角がそれぞれ等しい」というものがあります。
その条件を満たす三角形は合同だということ。
すなわち、そのような三角形は、この世に1つしかないということです。
この世に1つしかない三角形ならば、残る1つの角の大きさと2つの辺の長さは定まっているでしょう。
それを計算できるのが、正弦定理です。
残る1つの角は、三角形の内角の和が180°であることから、楽々と計算できます。
あとは、正弦定理を用いれば、残る2辺の長さは簡単に出てきます。
ヽ(^。^)ノ
問題 ⊿ABCにおいて、a=3、A=60°、B=45°のとき、bおよび外接円の半径Rを求めよ。
A=60°、a=3がわかっていますから、正弦定理を用いますと、他の辺の長さを求めることができます。
正弦定理により、
3/sin60°=b/sin45°
これをbについて解けば良いのですね。
しかし、分数計算が苦手な子は、この先で苦労しがちです。
教科書や問題集の解説は、この後の計算過程の解説が雑です。
まさか高校生が分数が苦手とは思っていないからでしょうか。
でも、多くの高校生は、正弦定理がわからないわけではないのです。
その先の分数計算が上手くできないのです。
絶対安全なやり方としては、分数=分数 の形の式になったときは、
左辺の分子×右辺の分母=右辺の分子×左辺の分母
という、たすきにかけた形の等式に直すと、あとの処理が楽です。
a/b=c/d のとき、ad=bc です。
これは、比例式、a:b=c:d のとき、内項の積=外項の積で、
ad=bc
とするのと同じ考え方です。
上の問題で言えば、
b・sin60°=3・sin45°
と書き換えます。
sin60°=√3/2、sin45°=1/√2 ですから、
√3/2・b=3・1/√2
b=3/√2×2/√3
=6/√6
=√6
この通りの計算手順でなければならないわけではないのです。
計算ルールとして間違っていなければ、他のやり方でも良いのです。
しかし、計算が苦手な子ほど、なぜかsinの値を早めに代入してしまい、分数の分母がさらに分数という繁分数に自分でしてしまう傾向があります。
そして、その処理方法がわからなくて行き詰まってしまうのです。
そんなときには、
「分数は、割り算に直せるよ。分子÷分母だよ。上÷下だよ」
とアドバイスするのですが、既にパニックを起こしていて、2を3と書き間違えるようなケアレスミスを繰り返し、何度解き直しても、どうにもこうにも正答に至らないということが起こりがちです。
あるいは、この問題は分子であるbがわからないのでまだ楽なのですが、分母であるsinの値を求める問題になると、式をどのように変形して良いかわからなくなる人は多いです。
そうした人のためにも、上のように、「分数=分数」の式を「かけ算=かけ算」の式に変形しておくことをお薦めします。
そうすれば、その先は、どの問題も同じ解き方になるので、いちいち考えなくて済むのです。
もしも、うっかり繁分数にしてしまい、行き詰まって、しかも分子÷分母を忘れてしまったら、1/3を思い出してください。
1/3は、1÷3ですか?それとも、3÷1でしょうか?
1÷3ですよね。
それで、「分子÷分母だ」と思い出すことができます。
(*^^)v
さて、外接円の半径Rも求めるのでした。
これも正弦定理により、
2R=3/sin60°
=3÷√3/2
=3×2/√3
=6/√3
=6√3/3
=2√3
R=√3
この辺りも、代入後の分数の処理、そして、分母の有理化で手間取る高校生は多いです。
でも、計算しやすいように式を変形することを覚えるだけで、随分楽になります。
計算が得意な人は、楽に計算できる方法で計算しています。
困難で複雑な計算方法に立ち向かっていったりはしていないのです。
2017年11月20日
高尾山から南高尾を歩いてきました。2017年11月
2017年11月19日(日)、高尾山から南高尾を歩いてきました。
朝、高尾山口駅を降りたときからもう混雑しています。
今は高尾山が1年で一番混雑するシーズン。
朝のうちに高尾山頂を通り抜けないと、渋滞に引っかかるぞー。
リフトの切符売り場も大行列でした。
PASMOで切符を購入できる販売機に並んだのですが、3人ほど前の人が、「大人片道2枚、子ども1枚」の切符を購入するのに5分ほどもかかっていました。
観光シーズンの観光地には、世慣れていない人がいます。
前の人がどのように購入しているか、見ておくと良かったのになあ。
購入ボタンを押してからPASMOをかざすというやり方は、初めてだと確かに戸惑います。
販売機にその説明は書いてあるのですが、焦ると説明は目に入らなくなるし。
2種類の切符を複数枚買うのなら、人が手売りしてくれる窓口に並んだほうが楽に購入できたでしょう。
でも、そういうことを即断即決で的確に判断する社会性というものは、観光地には似つかわしくないのかもしれません。
このようにして、観光シーズンの観光地の混雑がさらに激化していくのは、まあ仕方ないか。
急な階段を上がっていくと、リフトはそれほど長い行列にはなっていませんでした。
前に並ぶカップルの女の子が、
「私、リフトから落ちたことある。リフトが全部止まっちゃって、恥ずかしかったー」
ええ?と思い、きき耳をたてますと、スキー場のリフトでのことのようです。
スキーを落として流してしまう人はいるけど、本人が落ちるのはレアケースでは?
無事で良かったなあ。
そんなことが起こるくらいなら、切符の自動販売機で5分くらい余計に待たされるのは、何でもありませんね。
「リュックは前に提げてください」
「ベルトに立ったら、そのまま、歩かないでください」
係員さんは二人体制で指示していました。
さて乗車。
高尾山のエコーリフトは、登りよりも下りのほうが見晴らしがよくて好きなのですが、帰りはいつも大行列になっていて、なかなか下りには乗れません。
6分ほどで山頂駅。
リフトを降りるときは、いつも少し緊張します。
つまずいて転んだら、どうしよう。
でも、今回も無事に降り立つことができました。
リフト山頂駅。8:55。
支度をして出発。
1号路も朝から混雑しています。
山頂近くの、3号路との分岐にある大きなトイレも行列ができていました。
観光シーズン、凄いなあ。
山頂。9:40。
富士山は尖った雲をまとって、険悪な様相。
現地は荒れた天候でしょう。
丹沢は晩秋の色。
秋の朝の明瞭な視界の下、深い紫に茶色が混じった山肌は、少し怖いような印象でした。
紅葉は、今年はやはりダメですね。
それでも、肉眼で見る限りはきれいです。
朝の光に透かして見れば特に。
若い女の子2人が、撮った写真を見ながら、大声で喋っています。
「わあ、きれいだよ。こんなに大勢人がいるのに、主役感、凄いよ」
・・・若い女の子の感覚は、面白いなあ。
周りはモブ扱いかあ。
今日だけは自分が主役とか、写真の中では自分が主役とか、そういうことは、いつかどうでもよくなるよ。
人はいつでも主役だし、また、常に脇役だよ。
なんてね。
さて、石段を下りて、ここより奥高尾。
急に人が少なくなり、紅葉台からの下りの木段を淡々と降りていきました。
一丁平。10:10。
上の画像は、一丁平のベンチから奥を撮ったものです。
ここから、今日は南高尾に回ります。
まずは大平林道へ。
あずまやを左に見て、細い道を行きます。
突当りを左に折れて、あと道なりに進みます。
9月には夏草で塞がれていた道も、草が枯れ、歩きやすい良い道に変わっていました。
大平林道に降り立つと、すぐ右手に道しるべがありました。
「大垂水」と示す方向の通りに大平林道と別れ、斜面につけられた細い道に入りました。
やがて道が少し広くなり、コンクリートの階段が現れ、そこから甲州街道を渡る歩道橋と直接つながって、南高尾への道へ。10:40。
甲州街道が樹間から透けて見えるのでちょっと怖い崖っぷちの細い道をしばらく進み、そこから上り坂が続きます。
春夏は暑くてつらい道ですが、気温の低い今日は、気持ちよく登っていけました。
大洞山。11:05。
ここから先は、秋は特にしみじみとして好きな道です。
茶色の落ち葉に赤や黄色の葉が彩りを添える道を踏みしめて、ゆっくりと歩いていきました。
少し前を行く登山者の、つばの狭い生成りの帽子と、なで肩に古い型のザックを背負った後ろ姿が、秋の道に似合っていました。
展望台。11:45。
津久井湖とその周辺が箱庭のように見渡せるベンチで昼食。
ぽかぽかと日差しか暖かく、1枚羽織る必要もなく食事ができました。
ポットには熱いコーヒーを詰めてきました。
担いでいるスポーツドリンクの分量も少なくて済むし、秋から冬の山歩きはいいなあ。
さて、再び出発。
細い道をトレイルランナーとすれ違います。
今日の南高尾は、登山客は少ないけれど、トレイルランナーが多いです。
三沢峠。12:45。
ここはまき道も含めて5叉路の道。
ベンチもあって、休憩適地です。
「高尾山口」の道しるべの通りに上り坂を行くと、東高尾の遊歩道と合流します。
道は広く、階段が整備されています。
急な階段をどんどん降りて、最後に登ると、草戸山。13:15。
ここは、いつも通りに人で賑わっていました。
ベンチに座って見上げると、葉の落ちた木に柿の実がいくつか残っています。
青い空と柿の実に見とれていると、お尻に何か気配があり、振り返ると、あ、犬だ。
「すいませんっ」
と飼い主さんが、リードを縮めました。
さて、下山。
高尾山口へは、植林帯の暗い下りから始まりますが、すぐに日差しの明るい尾根道へと変わります。
この時間に登ってくる人が意外に多いのは、混雑を避けてのことでしょうか。
時差登山。フレックスかな。
途中の道しるべに、
「四辻より先、高尾駅を示す誤った落書きによる道迷いが発生しています」
という掲示が提げられていました。
四辻から京王線高尾山口駅に降りる道と別れ、まっすぐ進むJR高尾駅への道があります。
随分前に私も一度歩きました。
下山口を見つけるのが難しかった記憶があります。
人があまり歩かないので、この季節は落ち葉が積もり、もっと不明瞭でしょう。
そういうときに間違った落書きを残していくのは、ひどいなあ。
四辻まで来ると、12月2日(土)、南高尾を回り、笹尾根を登って数馬がゴールのトレイルランニングの大会が行われるという掲示がありました。
だからトレイルランナーが多かったんですね。
距離は、42km。
外秩父七峰と同じ距離だけど、アップダウンから考えると、これは走れるところでは走らないと1日では無理だろうなあ。
四辻から、高尾山口へ。
あっという間に高尾の信号前に出て、観光客でごった返す駅前へと戻ってきました。14:35。
2017年11月17日
三角比と関数の融合問題。

三角比と関数の融合問題を今回は扱ってみましょう。
問題 0°≦x≦180°のとき、 y=2sin2x-2cosx-1 の最大値と最小値を求めよ。
小学生や中学生は、文章題を見ると、
「問題が6行も書いてある。こんなの解けるわけない」
と、問題文の長さだけで解くのを諦めたりします。
あるいは、中学数学の関数や図形問題で、前提となる問題文を読まず、(1)の短い設問とグラフや図だけを見て、
「わからない、わからない。難しい」
とうんうんうなっている子も、珍しくありません。
問題文を読む習慣のない子は、かなりの割合で存在します。
どうせ大したことは書いていないと思っているのでしょうか。
文字を読み取ること自体が苦痛なので、できるだけ省略したいのでしょうか。
そういうタイプの問題は、問題文を読まないと解けるわけないんですけど。
(^-^;
しかし、高校の数学には、もっと別の怖さがあります。
しかし、高校の数学には、もっと別の怖さがあります。
こういう問題文が1行だけの問題が増えてくるのです。
何行も問題文が書いてあれば、どこかにヒントがありますが、こんなふうに1行で終わられたら、何もとっかかりがありません。
何をどうしたらいいのかわからない、という事態に至ります。
何行も問題文が書いてあれば、どこかにヒントがありますが、こんなふうに1行で終わられたら、何もとっかかりがありません。
何をどうしたらいいのかわからない、という事態に至ります。
問題が何を言っているのか、わからない。
何を要求しているのか、わからない。
何をどうすることがこの問題を解いたことになるのか全くわからない、ということが起こりうるのです。
教わったときだけは何とか解き方を暗記しても、2か月も経って、校外実力テストや模試でこういう問題が出ていると、この1行を見つめたまま固まることになります。
そんな高校生は、多いです。
高校数学に白紙答案があるのは、そういう理由です。
わざと解かないわけではない。
どう解いたら良いのか、本当に何もわからないのでしょう。
そんな高校生は、多いです。
高校数学に白紙答案があるのは、そういう理由です。
わざと解かないわけではない。
どう解いたら良いのか、本当に何もわからないのでしょう。
この問題は、
「最大値・最小値って、関数で出てくる用語だよね」
と気づくと、問題がほぐれてきます。
そう思って見ると、
y=2sin2x-2cosx-1
って、関数ですよね。
これと似ている関数のイメージは、
y=2x2-2x-1
だから、ああ、これは2次関数なのだと気づきます。
しかし、普通の2次関数と違うのは、xではなく、sinxとcosxが使われていること。
うん?
それは、書き換えられたんじゃなかったでしたっけ?
サインはコサインに、コサインはサインに、転換する方法がありましたよね。
ここで、三角比の相互関係の公式を用いるのだと気づけば、もう先は見えてきました。
公式は、こうです。
sin2θ+cos2θ=1 (2は指数)
すなわち、
sin2θ=1-cos2θ
今回は、角度はθではなく、xが使われていますから、
sin2x=1-cos2x
これを代入します。
y=2sin2x-2cosx-1
=2(1-cos2x)-2cosx-1
y=2sin2x-2cosx-1
=2(1-cos2x)-2cosx-1
=2-2cos2x-2cosx-1
=-2cos2x-2cosx+1
ああ、これは2次関数ですねえ。
慣れてくるとこのままでも先に進めますが、見やすくするため、cosx=t と置き換えてみましょう。
すなわち、
y=-2cos2x-2cosx+1
=-2t2-2t+1
これの最大値と最小値を求めたらいいんだー。
ヽ(^。^)ノ
しかし、その先もそう簡単にはいかない人がいます。
「三角比」の学習に入る頃には「2次関数」で学んだことの大半を忘れてしまっている子が多いのです。
数学は積み上げ科目なので、一度学習したことは忘れたらダメなのですよー。
2次関数の最大値と最小値の求め方?
何をどうするんでしたっけ?
2次関数のグラフは放物線です。
まずは定義域を無視して考えるのなら、頂点の y 座標が最小値か最大値になります。
下に凸の放物線ならば、頂点の y 座標が最小値。
上に凸の放物線ならば、頂点の y 座標が最大値。
頂点の座標を求めるためには、平方完成をします。
平方完成のやり方、覚えていますか?
高校生が相手ですと、ここでまたドタバタ。
平方完成という言葉すら忘れていたりします。
y=-2t2-2t+1
=-2(t2+t)+1
=-2(t+1/2)2+1/2+1
=-2(t+1/2)2+3/2
すなわち、頂点の座標は、(-1/2 , 3/2) となりますから、
t=-1/2のとき、最大値3/2となります。
ところで、これは、定義域にある数なのか?
y=-2cos2x-2cosx+1
=-2t2-2t+1
これの最大値と最小値を求めたらいいんだー。
ヽ(^。^)ノ
しかし、その先もそう簡単にはいかない人がいます。
「三角比」の学習に入る頃には「2次関数」で学んだことの大半を忘れてしまっている子が多いのです。
数学は積み上げ科目なので、一度学習したことは忘れたらダメなのですよー。
2次関数の最大値と最小値の求め方?
何をどうするんでしたっけ?
2次関数のグラフは放物線です。
まずは定義域を無視して考えるのなら、頂点の y 座標が最小値か最大値になります。
下に凸の放物線ならば、頂点の y 座標が最小値。
上に凸の放物線ならば、頂点の y 座標が最大値。
頂点の座標を求めるためには、平方完成をします。
平方完成のやり方、覚えていますか?
高校生が相手ですと、ここでまたドタバタ。
平方完成という言葉すら忘れていたりします。
y=-2t2-2t+1
=-2(t2+t)+1
=-2(t+1/2)2+1/2+1
=-2(t+1/2)2+3/2
すなわち、頂点の座標は、(-1/2 , 3/2) となりますから、
t=-1/2のとき、最大値3/2となります。
ところで、これは、定義域にある数なのか?
そもそも定義域ってあったっけ?
この確認は大切です。
t の定義域って?
cosx=t としたのですから、その定義域を考えればよいわけです。
問題の最初に書いてある通り、0°≦x≦180°なので、
cosxの変域は、-1≦cosx≦1。
すなわち、-1≦t≦1。
高校生は、ここでさらにドタバタ。
コサインの変域ということが、どうにもこうにも理解できない人が現れます。
そこで、単位円を描いて、もう一度、コサインの定義から説明し直しとなる場合が多いです。
この確認は大切です。
t の定義域って?
cosx=t としたのですから、その定義域を考えればよいわけです。
問題の最初に書いてある通り、0°≦x≦180°なので、
cosxの変域は、-1≦cosx≦1。
すなわち、-1≦t≦1。
高校生は、ここでさらにドタバタ。
コサインの変域ということが、どうにもこうにも理解できない人が現れます。
そこで、単位円を描いて、もう一度、コサインの定義から説明し直しとなる場合が多いです。
半径1の単位円上の点をP(x,y)とし、動径OPとx軸の正の方向とのなす角をθとすると、
cosθはxの値そのものでした。
ですから、θ=0°のとき、すなわち、OPはx軸が重なっているときは、P(1,0)ですから、
cos0°=1
θ=90°のときは、P(0,1)ですから、
cos90°=0
θ=180°のときは、P(-1,0)ですから、
cos180°=-1
このように、0°≦θ≦180° のとき、-1≦cosθ≦1 です。
さて、コサインの変域が理解できたので。
定義域は、-1≦t≦1。
おお、t=-1/2は、定義域内に入っていますね。
これで、最大値は確定です。
ところで、最大値を答えるときは、xが何の値のときにyが最大値になるのかも答えなければなりません。
t=-1/2
すなわち、cosx=-1/2
頭の中で単位円を想像して。
それがまだ無理なら、実際に単位円を描いて。
cosx=-1/2
すなわち、x=120°
次に最小値を考えます。
放物線は、左右対称です。
今、放物線は上に凸。
頂点から離れるほどに、急激に y の値は小さくなっていきます。
tの変域の内部で、頂点の t の値-1/2から距離があるほうの端の値が、最小値となります。
-1と1。
-1/2から遠いのはどちらか?
もちろん、1ですね。
ですから、t=1のとき最小値です。
t=1を代入して、
y=-2t2-2t+1
=-2-2+1
=-3
さて、t=1すなわち cosx=1のとき、
またまた、単位円をイメージして。
x=0°
したがって、
x=120°のとき最大値3/2
x=0°のとき最小値-3
これが最終解答となります。
問題に出てくるxとyと、コサインの定義に出てくるxとyとで混乱が起こる人もいます。
cosθならばわかるけれど、cosxと書いてあるだけで、何のことかわからなくなる人もいます。
「そんなところでxを使っていいんですか?」
と不安になり、納得できない様子なのです。
「きちんと定義してあれば、どんな文字だって使っていいでしょう」
そう説明しても、頭の中の霧は晴れない様子です。
数学が苦手な人の頭の中を覆うこうした「霧」の正体は何なのか。
xやyなど、文字が数学に登場した頃から、実は納得できていなかったのではないか?
何か使い方にルールがあるはずなのに、自分だけそのルールが理解できないでいる。
そんな不安があるのだろうかと想像してみるのですが、まだよくわからないことが多いです。
生徒の言葉の端から想像してみるしかないのです。
わからないことの何がどのようにわからないのかを明確に語ることができるのなら、それは「わかっている」のと同じでしょう。
何がわからないのかわからないから、本人も悩んでいるのだと思います。
不安は、比較的理解力のある高校生の中にもあるようです。
わからないわけではない。
説明を聞けばわかるのです。
でも、自分で解こうとすると、途中で詰まってしまう。
あれ、何のことだっけ?
今、何をやっていたんだっけ。
そうやって何度も詰まる。
そんな感想の人もいると思います。
でも、自分で解こうとすると、途中で詰まってしまう。
あれ、何のことだっけ?
今、何をやっていたんだっけ。
そうやって何度も詰まる。
そんな感想の人もいると思います。
わからなくなる度、なぜそれで解けるのかを考え直し、頭の中に明瞭な筋道を作っていきましょう。
作業手順だけ覚えてやり過ごそうとしても、作業手順が長すぎて、覚えきれないです。
作業手順だけ覚えてやり過ごそうとしても、作業手順が長すぎて、覚えきれないです。
覚えることは、これだけではないのですから。
思うに、希望はあるものとも言えぬし、ないものとも言えない。
歩く人が多くなれば、それが道になるのだ。
歩くのが自分一人ならば、何回も歩けば、それは道になります。
ヽ(^。^)ノ
2017年11月13日
払沢の滝から浅間尾根を歩きました。2017年11月。
2017年11月12日、久しぶりに山を歩いてきました。
ホリデー快速あきがわ3号に乗車し、終点武蔵五日市下車。
駅前発の数馬行きのバスは3台同時発車でした。9:00。
本宿役場前下車。9:20。
三叉路を左に曲がっていくバスを見送り、横断歩道を渡って右のゆるい坂道を登ると、有名なお豆腐屋さん。9:30。
車を誘導する人が立っていました。
観光シーズンですね。
看板の矢印通りに、まずは払沢の滝を見物。
整備された遊歩道を奥へと歩いていきます。
今年は夏の日照時間が不足していましたから、紅葉はそれほどきれいではないでしょう。
でも、あまり期待しないで行くと、赤が鮮やかに出ている木もあり、何だか得をした気分になりました。
少ないものをしみじみと味わう気持ちになります。
遊歩道の突当りが、払沢の滝。9:40。
写真好きの人たちが三脚を立て、既にスタンバイ完了の状態で待機していました。
これから滝に陽が差してきたら、シャッターチャンスなのでしょうか。
滝壺まで岩の階段を上がって行くことができます。
近場でじっくり滝を見物。
その後、あずまやでひと休み。
そうして、のんびり来た道を戻りました。
遊歩道の入り口まで戻ると、浅間尾根への道しるべがあります。
その通りに歩いていくと、まずは駐車場。
ペーパーの設置されたきれいなトイレがありました。
駐車場の端から山道の始まりです。
林道と、林道をショートカットする細い山道が繰り返され、高度を上げていきます。
向こうに見える隣りの尾根の山の色も、秋の色。
赤紫に霞んでいました。
時坂峠を越えて、さらに林道を行くと、峠の茶店。
その先、徒歩5分ほどで、そば処みちこ。
今日はここでお昼ご飯です。11:00。
山道を徒歩1時間の蕎麦屋というとかなり秘境の印象です。
でも、ここまで舗装された林道が通り、駐車場もありますので、車で来ている人も多いようです。
2年ほど前に通りかかったときと比べ、表の垣根の色合いも随分ひなびて良い雰囲気でした。
しかし、店内は、アンジャッシュ渡部の写真入り色紙などが壁にずらっと飾られてありました。
ああ、こういう感じかあ。
ちょっとがっかり。
「秘境飯」系のテレビ番組の取材を受けることが多いのでしょうか。
ちょっとがっかり。
「秘境飯」系のテレビ番組の取材を受けることが多いのでしょうか。
メニューは冷たいお蕎麦が3種類。季節限定の温かいきのこ蕎麦が1種類。
全て、天ぷら付きにできます。
私は、手打ち二八蕎麦、天ぷら付。1200円を注文。
私の前に立て続けに3組、客が入っていたこともあり、店に入ってからお蕎麦がテーブルに出てくるまで、所要時間40分。
全て、天ぷら付きにできます。
私は、手打ち二八蕎麦、天ぷら付。1200円を注文。
私の前に立て続けに3組、客が入っていたこともあり、店に入ってからお蕎麦がテーブルに出てくるまで、所要時間40分。
ぶつ切りの太目の蕎麦でした。
味は普通においしいお蕎麦と天ぷらでした。
浅間尾根に登るときには、また寄ろうかな。
さて、12:00、出発。
ここからは、ずっと山道です。
まずは沢に沿い、やがて沢と離れ、高度を上げていきます。
陽の光が差すと、赤い葉がきれいです。
黄色い葉のほうは、どの年も安定してきれい。
落ち葉の積もった山道を向こうからやってくる登山者と、挨拶を交わしてすれ違います。
しみじみと、秋です。
展望台との分岐。
このまま直進しても浅間尾根の休憩園地に到着しますが、展望がいいのは「展望台」と道しるべに記されている尾根道のほうです。
道しるべに従い、そちらへ。
しかし、広くなだらかな斜面に落ち葉が深く積もっていて、途中で登山道がよくわからなくなりました。
道のように見えてはいるけれど正規の登山道ではないところに、気がつくと迷い込んでいました。
落ち葉に覆われた足元は、まあまあ固いので、人が歩いていないところではなさそうです。
作業道かな。
それでも、日差しが明るいので、あまり慌てずに済みました。
尾根は見えている。
あそこに上がれる道を探そう。
無理はせずに、足元を確かめながら、歩ける道を行こう。
登っていくと、遠くに道しるべが見えて、安全にそこまでたどりつくことができました。
ああ、正規の道は、やはりずっと固い。
浅間尾根展望台。13:00。
向いの尾根の大岳山と御前山を山座同定できる杭は変わらずです。
ベンチやテーブルが新しく設置されていました。
煮炊きが楽にできるようになったので、登山者でにぎわっています。
2年来ないと山は変わりますね。
便利なんだけれど、ふっと寂しくなったりします。
ごつごつした石に座ってお昼を食べた、あまり人のいない浅間尾根も好きだったな。
ベンチに座り、山を眺めました。
秋の色です。
上の写真はそこで撮りました。
さて下山。
下り道も整備されて歩きやすくなっていました。
前回は園地に降りて、そこからまき道を行きましたが、今回は尾根通しに歩いてみることにしました。
多少わかりにくいところもありましたが、さっき迷ったので慎重に踏み跡を探したこともあり、迷わず降りていけました。
その先、崖っぷちの細い道もときどきあり、注意してそろそろと通過する箇所もありましたが、概ねよく整備された道が続きます。
数馬分岐。14:30。
ここで浅間尾根と別れ、檜原街道へと降りていきます。
この下り道も整備された歩きやすい道でした。
やがて舗装道に出て、道なりにぐっと下っていくと、檜原街道に合流。
そこからは、バス停2つ分歩いて、檜原温泉センター数馬の湯へ。15:30。
靴を脱いで、下駄箱に入れようとして、あれ?
100円を投入して、後で戻ってくるタイプの下駄箱でした。
前からそうでしたっけ?
うわあ、財布に100円玉がない。
まずは両替をしてもらうために受付の行列に並び、その後、下駄箱の鍵を手にもう一度受付に並ぶという二度手間になってしまいました。
お蕎麦屋さんで、おつりなしで支払いしなければ良かったー。
というより、もっと小銭の用意を、ということですね。
お風呂は、シャンプーとボディソープの質が良くなっていました。
泡立ちがいい。
湯舟は安定の快適さです。
ここは、内風呂が良いんです。
高窓から見える山を眺めながら、深めの浴槽に首までしっかりつかります。
はあ、山の温泉も久しぶりだあ。
お風呂から上がり、缶ビール500mL420円。
飲み終わって、温泉センター前のバス停の行列に並びました。
「都民の森」発のバスは、4台同時にやってきました。
4台目で座ることができました。16:09。
観光シーズンなので、十里木を過ぎたあたりから道は渋滞しましたが、終点武蔵五日市駅でバスを降りると、ちょうどホリデー快速あきかわ6号に間に合いました。17:21。
三鷹まで1本で、18:09、予想外に早く帰宅できました。
2017年11月09日
三角比の拡張。ここで三角比は生まれ変わります。
三角比の始まりは、直角三角形の辺の比です。
非常に便利なのですが、直角三角形である限り、∠θは鋭角なので、限定的です。
何とか鈍角でも三角比は使えないでしょうか?
はあ?
直角三角形に鈍角なんてあるわけないし!
そんな反応も予想できます。
それは当然そうなのですが、とにかく便利なので、使えるようにしたいのです。
その発想が原点です。
とにかく、1つのことが言えたら、それを一般化したいのです。
特殊相対性理論が言えたら、一般相対性理論。
何事においても、限定解除が理想です。
鈍角の三角比は、単位円を描いて考えます。
高校1年の数Ⅰ「三角比」では、まだ∠θは0°から180°までなので、上半分だけで大丈夫です。
単位円とは、座標平面上に描いた、原点を中心とした半径1の円です。
この円周上を動く動点Pの座標を(x,y)とします。
中心と結んだ線分OPを動径と呼びます。
「動く半径」ですね。
Pを円周上のどこにとってもOPは円の半径ですから常に1です。
Pからx軸に垂線を下ろします。
そうすると、上の図のような直角三角形を座標平面上に描くことができます。
斜辺は半径ですから、長さは1です。
P(x,y)ですから、この直角三角形の対辺の長さはy、底辺の長さはxとなります。
動径とx軸の正の方向との成す角をθとすると、
sinθ=y/1=y
cosθ=x/1=x
tanθ=y/x
となります。
これは便利です。
サインがy座標そのもの、コサインがx座標そのものになりますから。
このように、三角比を定義し直します。
原点Oを中心として半径rの円において、x軸の正の向きから左まわりに大きさθの角をとったとき定まる半径をOPとし、点Pの座標を(x,y)とする。このとき、
sinθ=y/r , cosθ=x/r 、tanθ=y/x と定める。
というのが、拡張した三角比の定義です。
実際には、
上のようにr=1のとき、サインがy座標そのもの、コサインがx座標そのもの、タンジェントは直線OPの傾きそのものになり、とても便利なので、この単位円で話を進めていきます。
数学が苦手な高校生は、中学の頃から関数が苦手なことが多いです。
上の説明では、直角三角形の対辺がyになり、底辺がxになるところが理解しにくい様子です。
座標と線分の長さとが頭の中で上手くつながらないようなのです。
中学の数学の座標平面と図形に関する問題も、そこが頭の中でつながらないせいでほとんど得点できない子が多いです。
「これは応用問題だから、自分はできなくても仕方ないやあ」
などと軽く考えて避けていると、高校生になるとそこが基本になるので、訳がわからなくなっていきます。
理解できないので、ただ暗記するだけになるのです。
つい先日も、中学生との数学の授業で、点Pのx座標をtと置いて、座標平面上の正方形の辺の長さをtを用いて表し、最終的にPの座標を求めるという典型題の解説・演習をしていたのですが、
「勝手にtと置いたのに、何でtの値がわかるんですか?」
「tは定まっていないのに、何でtを求めていいんですか?」
という、わかるようなわからないような疑問で頭がねじれてメビウスの輪になっている子と議論しました。
ここのところがどうしてもわからない子と、一度でスルッと理解する子との違いは何なのだろうといつも不思議に思います。
単位円の話に戻りましょう。
「単位円上の動点Pの座標を(x,y)とする」というのは定義であるのに、
「どうしてそうなるんですか?」
「点Pが円周上にないときはどうするんですか?」
といった不要な質問で頭がいっぱいになって、理解できなくなる人がいます。
それは定義なんだから、疑義を挟むところではないんです。
定義というのは決めたことで、理由はないんです。
あえて言えば、そう定義することで後々便利だからです。
しかし、そう言っても、納得できない様子です。
xやyというのは、もっと使い方に別のルールがあって、そこで勝手に使ってはいけないのではないか?
そういう思い込みがあるのかもしれません。
繰り返しますが、これは定義です。
単位円上の動点Pの座標を(x,y)とすることには、何の問題もありません。
「単位円上の動点」と決めたので、点Pは、そこから外れることもありません。
話を戻しましょう。
sinθ=y
cosθ=x
tanθ=y/x
このように定義し直したら、もう直角三角形から離れ、三角比は1人歩きできます。
座標平面の第2象限、すなわち、単位円の半円の左側に動径OPが来ても、同じ定義が可能です。
それで鈍角の三角比を求めることができます。
サインは、点Pのy座標そのもの。
コサインは、点Pのx座標そのもの。
タンジェントは、直線OPの傾き。
そう把握できるのです。
点Pが第2象限にあるとき、反対向きの直角三角形を描き、その辺の比を求めようとしてサインとコサインがグチャグチャになってしまう高校生がいます。
うんうんうなりながら、鏡の中で反転している直角三角形と格闘しているのですが、そういうことではないんです。
∠θはあくまでも、x軸の正の方向と動径OPとの成す角です。
考えるヒントとして反対向きの直角三角形を描いて解説するのは、第1象限の直角三角形とy軸に対して線対称であることを示すためです。
線対称だから、第1象限に置き換えて考えましょうと説明しているのですが、ノートに第2象限の直角三角形が残るせいか、そっちで求めるのだと誤解している人がいます。
第2象限の三角比は、絶対値を第1象限の直角三角形で把握し、それにプラス・マイナスの符号をつけて求めていくと楽です。
拡張された定義から明らかですが、サインはyの値ですから、相変わらず正の数です。
コサインはxの値ですから、負の数。
タンジェントもxの値が負の数であることが影響し、負の数となるでしょう。
考えるヒントとして反対向きの直角三角形を使いたい人は使えばよいのですが、それで混乱するのは無駄なことだと思います。
あげく、「鈍角の左側の直角三角形の辺の比を求めること」と思い込み、「三角比とは直角三角形の辺の比である」というところから全く飛翔できず、三角形の面積を求める頃になって「直角三角形以外では、三角比は使えないですよっ」と言い張る高校生と不毛な議論をしたこともあります。
実際の問題で考えてみましょう。
例えば、∠θ=120°のとき。
P(x,y)は、∠θ=60°のときのPと、y軸について線対称です。
∠θ=60°のとき、特別な比の直角三角形をイメージして解くと、
sinθ=√3/2 , cosθ=1/2 , tanθ=√3 /1=√3 ですから、
∠θ=120°のときは、
sinθ=√3/2 , cosθ=-1/2 , tanθ=-√3 となります。
慣れてしまえば、いちいち描かなくても、頭の中で特別な比の直角三角形をイメージするだけで解けます。
上手くイメージできない間は、第1象限に直角三角形を描いて解いても良いでしょう。
スラスラっと説明してきましたが、ここら辺になると、つまずく石は無数に存在し、
「足元に気をつけて!」
と注意し続けながら授業を先に進めるような状況となってきます。
いったん理解したはずなのに、ここでパニックを起こし、三角比は角度のことだと錯誤し、混乱し始める子もいます。
「苦手な図形」と「大嫌いな関数」が合体したのですから、地獄巡りの心境の子がいるのも無理からぬところです。
すぐに定義が曖昧になり、何でそれで求められるかわからなくなってしまう子が続出します。
とにかく学校の問題集だけ解きたい、学校の問題集を解いて提出しなければならないから、その問題だけを解きたい。
そんな高校生がどんどん増えていきます。
でも、敗退にはまだ早い。
まだ、常人に理解できる範囲の数学です。
繰り返し繰り返し、意味に戻って理解し直せば、三角比は必ずマスターできます。
非常に便利なのですが、直角三角形である限り、∠θは鋭角なので、限定的です。
何とか鈍角でも三角比は使えないでしょうか?
はあ?
直角三角形に鈍角なんてあるわけないし!
そんな反応も予想できます。
それは当然そうなのですが、とにかく便利なので、使えるようにしたいのです。
その発想が原点です。
とにかく、1つのことが言えたら、それを一般化したいのです。
特殊相対性理論が言えたら、一般相対性理論。
何事においても、限定解除が理想です。
鈍角の三角比は、単位円を描いて考えます。
高校1年の数Ⅰ「三角比」では、まだ∠θは0°から180°までなので、上半分だけで大丈夫です。
単位円とは、座標平面上に描いた、原点を中心とした半径1の円です。
この円周上を動く動点Pの座標を(x,y)とします。
中心と結んだ線分OPを動径と呼びます。
「動く半径」ですね。
Pを円周上のどこにとってもOPは円の半径ですから常に1です。
Pからx軸に垂線を下ろします。
そうすると、上の図のような直角三角形を座標平面上に描くことができます。
斜辺は半径ですから、長さは1です。
P(x,y)ですから、この直角三角形の対辺の長さはy、底辺の長さはxとなります。
動径とx軸の正の方向との成す角をθとすると、
sinθ=y/1=y
cosθ=x/1=x
tanθ=y/x
となります。
これは便利です。
サインがy座標そのもの、コサインがx座標そのものになりますから。
このように、三角比を定義し直します。
原点Oを中心として半径rの円において、x軸の正の向きから左まわりに大きさθの角をとったとき定まる半径をOPとし、点Pの座標を(x,y)とする。このとき、
sinθ=y/r , cosθ=x/r 、tanθ=y/x と定める。
というのが、拡張した三角比の定義です。
実際には、
上のようにr=1のとき、サインがy座標そのもの、コサインがx座標そのもの、タンジェントは直線OPの傾きそのものになり、とても便利なので、この単位円で話を進めていきます。
数学が苦手な高校生は、中学の頃から関数が苦手なことが多いです。
上の説明では、直角三角形の対辺がyになり、底辺がxになるところが理解しにくい様子です。
座標と線分の長さとが頭の中で上手くつながらないようなのです。
中学の数学の座標平面と図形に関する問題も、そこが頭の中でつながらないせいでほとんど得点できない子が多いです。
「これは応用問題だから、自分はできなくても仕方ないやあ」
などと軽く考えて避けていると、高校生になるとそこが基本になるので、訳がわからなくなっていきます。
理解できないので、ただ暗記するだけになるのです。
つい先日も、中学生との数学の授業で、点Pのx座標をtと置いて、座標平面上の正方形の辺の長さをtを用いて表し、最終的にPの座標を求めるという典型題の解説・演習をしていたのですが、
「勝手にtと置いたのに、何でtの値がわかるんですか?」
「tは定まっていないのに、何でtを求めていいんですか?」
という、わかるようなわからないような疑問で頭がねじれてメビウスの輪になっている子と議論しました。
ここのところがどうしてもわからない子と、一度でスルッと理解する子との違いは何なのだろうといつも不思議に思います。
単位円の話に戻りましょう。
「単位円上の動点Pの座標を(x,y)とする」というのは定義であるのに、
「どうしてそうなるんですか?」
「点Pが円周上にないときはどうするんですか?」
といった不要な質問で頭がいっぱいになって、理解できなくなる人がいます。
それは定義なんだから、疑義を挟むところではないんです。
定義というのは決めたことで、理由はないんです。
あえて言えば、そう定義することで後々便利だからです。
しかし、そう言っても、納得できない様子です。
xやyというのは、もっと使い方に別のルールがあって、そこで勝手に使ってはいけないのではないか?
そういう思い込みがあるのかもしれません。
繰り返しますが、これは定義です。
単位円上の動点Pの座標を(x,y)とすることには、何の問題もありません。
「単位円上の動点」と決めたので、点Pは、そこから外れることもありません。
話を戻しましょう。
sinθ=y
cosθ=x
tanθ=y/x
このように定義し直したら、もう直角三角形から離れ、三角比は1人歩きできます。
座標平面の第2象限、すなわち、単位円の半円の左側に動径OPが来ても、同じ定義が可能です。
それで鈍角の三角比を求めることができます。
サインは、点Pのy座標そのもの。
コサインは、点Pのx座標そのもの。
タンジェントは、直線OPの傾き。
そう把握できるのです。
点Pが第2象限にあるとき、反対向きの直角三角形を描き、その辺の比を求めようとしてサインとコサインがグチャグチャになってしまう高校生がいます。
うんうんうなりながら、鏡の中で反転している直角三角形と格闘しているのですが、そういうことではないんです。
∠θはあくまでも、x軸の正の方向と動径OPとの成す角です。
考えるヒントとして反対向きの直角三角形を描いて解説するのは、第1象限の直角三角形とy軸に対して線対称であることを示すためです。
線対称だから、第1象限に置き換えて考えましょうと説明しているのですが、ノートに第2象限の直角三角形が残るせいか、そっちで求めるのだと誤解している人がいます。
第2象限の三角比は、絶対値を第1象限の直角三角形で把握し、それにプラス・マイナスの符号をつけて求めていくと楽です。
拡張された定義から明らかですが、サインはyの値ですから、相変わらず正の数です。
コサインはxの値ですから、負の数。
タンジェントもxの値が負の数であることが影響し、負の数となるでしょう。
考えるヒントとして反対向きの直角三角形を使いたい人は使えばよいのですが、それで混乱するのは無駄なことだと思います。
あげく、「鈍角の左側の直角三角形の辺の比を求めること」と思い込み、「三角比とは直角三角形の辺の比である」というところから全く飛翔できず、三角形の面積を求める頃になって「直角三角形以外では、三角比は使えないですよっ」と言い張る高校生と不毛な議論をしたこともあります。
実際の問題で考えてみましょう。
例えば、∠θ=120°のとき。
P(x,y)は、∠θ=60°のときのPと、y軸について線対称です。
∠θ=60°のとき、特別な比の直角三角形をイメージして解くと、
sinθ=√3/2 , cosθ=1/2 , tanθ=√3 /1=√3 ですから、
∠θ=120°のときは、
sinθ=√3/2 , cosθ=-1/2 , tanθ=-√3 となります。
慣れてしまえば、いちいち描かなくても、頭の中で特別な比の直角三角形をイメージするだけで解けます。
上手くイメージできない間は、第1象限に直角三角形を描いて解いても良いでしょう。
スラスラっと説明してきましたが、ここら辺になると、つまずく石は無数に存在し、
「足元に気をつけて!」
と注意し続けながら授業を先に進めるような状況となってきます。
いったん理解したはずなのに、ここでパニックを起こし、三角比は角度のことだと錯誤し、混乱し始める子もいます。
「苦手な図形」と「大嫌いな関数」が合体したのですから、地獄巡りの心境の子がいるのも無理からぬところです。
すぐに定義が曖昧になり、何でそれで求められるかわからなくなってしまう子が続出します。
とにかく学校の問題集だけ解きたい、学校の問題集を解いて提出しなければならないから、その問題だけを解きたい。
そんな高校生がどんどん増えていきます。
でも、敗退にはまだ早い。
まだ、常人に理解できる範囲の数学です。
繰り返し繰り返し、意味に戻って理解し直せば、三角比は必ずマスターできます。
2017年11月06日
中間テスト結果出ました。2017年2学期。

2017年2学期中間テストの結果が出ました。
数学 90点台 1人 80点台 1人 70点台 1人
60点台 1人 50点台 3人 30点台 1人
英語 100点 1人 90点台 1人 80点台 2人
60点台 1人 50点台 1人
50点未満が常連の人たちが、今回、50点を突破し、やったーと思っていたら、最後の最後で数学に30点台が1人出てしまい、予想外の展開でした。
でも、今回は、病気だったので仕方ないです。
また次回。
今回、良かったなあと思うことの1つは、
「テストまで、学校の問題集を1回解いてノートを完成させるだけ」
という学習習慣からの脱却が成功しつつあることです。
学校の問題集を1回解いたのが数学の勉強の全てで、成績が上がるわけないのですから。
そうでない授業を徹底すれば良いだけなんじゃないの?
と言われると、本当にその通りなのですが、なかなかそれが難しいのです。
入塾してくる生徒のうち、中高一貫校の生徒の大半は、数学の「体系問題集」を教えてほしくてやってくるのです。
中高一貫校の多くは「体系数学」という特殊な教科書を採用しています。
5年間で数Ⅲまでを終える、特別な構成の教科書です。
「三角比」と「三角関数」を一気に学習してしまうなど、類似の単元を一気にやるため、学習上の「無駄」が省かれます。
言い換えれば、反復がなされない教科書です。
一度つまずくと、それっきりです。
それでも、教科書「体系数学」は読み物としてなかなか丁寧な作りで、数学を独学する大人の人にはこの教科書の注文購入を勧めたいくらいです。
しかし、準拠問題集「体系問題集」は厄介です。
レベルAの問題は教科書「体系数学」で扱っている例題の類題が多いので、特に問題ありません。
しかし、レベルB、レベルCは、教科書で扱っていないパターンの難問が多数含まれています。
これを自習してノートを提出するのが学校の宿題となります。
詳しい解答・解説は学校から配られていますが、数学が苦手な子は、解説を読んでもわからないのです。
だから、個別指導で教えてほしい。
そういう生徒が入塾してきます。
つまり、入塾の目的が「体系問題集の解説」です。
「学校の問題集は扱いませんよ」
と言いにくい、というより、言えない。
そんな事情が最初に発生しています。
うちの塾で、数学で高得点をマークしている子たちは、中学生にしろ高校生にしろ、学校の問題集を塾で扱うことはありません。
体系問題集でも、それ以外でも、どんな問題集でどんなレベルのものがその子の学校の問題集であるかは把握していますが、内容を扱うことはありません。
学校の宿題は自分で解きます。
その他に塾テキストで学習し、塾の宿題を解きます。
余裕があれば、さらに自分で市販の問題集を買って解きます。
進度は学校に合わせて塾の授業を行っていますが、学校の教材は扱いません。
そのほうが、結果が出るからです。
立体的な学習となり、その単元の重要ポイントがわかります。
テストにどんな問題が出題されるかも、わかるようになっていきます。
何より、演習量の差は、露骨に得点に反映されます。
一方、体系問題集での授業を望んで入塾してくる数学が苦手な子たちは、
学校の宿題がわからないので解説してほしい。
一緒に解いてほしい。
それ以外のことはやりたくない。
とにかく宿題のノートを完成させたい。
そういう幅の狭い、視野の狭い学習に陥りがちです。
保護者の方は数学の成績が良くなることもあわせて希望していらっしゃるのですが、子どもは楽ができるとなると、どんどん甘えてきます。
ちょっとわからないと「塾で教わればいいや」と思い、深く考えなくなります。
宿題のノートが完成すると、理解できているように思ってしまう子もいます。
教わって解いた問題は全部自力で解けるような気がするのでしょうか。
家で解き直したり、別の問題集で類題を解いたりということは、なかなか自発的には行いません。
宿題のノートさえ完成すれば良いのです。
もともと、数学の勉強は嫌いなので、それ以上はやりたくないのです。
その意識のズレに、保護者の方はなかなか気づきません。
実際、この数年の間には、ちょっと困った生徒もいました。
先まで予習が進むと、塾を休むのです。
こちらは、先に先に学習を進めて、テスト前に復習の時間を作りたいと頑張ります。
そうやって必死に作った時間的余裕を、生徒が休んで空費してしまうのです。
学校の問題集の件が大丈夫である限り、塾を休むことが増えていきます。
何でそんなことを保護者が許可しちゃうのかなあ・・・・と思いますが、子どもが「大丈夫」と言う限り大丈夫と思いたい気持ちもわからないではありません。
これまで、テスト前の最後の授業も、体系問題集の中でもテストに出そうにない応用問題のページを解くことで終了することもありました。
テスト当日に提出する宿題ノートを完成させることが、数学のテスト勉強の全てでした。
そんなことですと、やがて成績が下がっていきます。
結果、塾をやめてしまうことにもつながったこともありました。
入会の目的が「体系問題集を教えてほしい」である子に、どうにか体系問題集以外のテキストをメインとした授業を行い、成績を上げ、納得してもらう。
体系問題集もできるだけ自力で解ける学力を養成する。
この難しい課題に、ようやく少しずつ解決策が見つかってきました。
授業中に、体系問題集も勿論扱います。
それでいて、演習量も確保します。
それをどうするかが解決できるようになってきました。
それが、今回の成績上昇につながったと思います。
期末は、さらに頑張っていきましょう。
2017年11月01日
三角比の相互関係の公式。覚えましょう。
三角比の当面の目標は、三角形の辺や角を計算せずに求めていくことです。
ならば、まずは三角比が1つわかれば残る2つが求められると便利です。
サインがわかれば、コサインやタンジェントは計算で求められる。
コサインがわかれば、サインやタンジェントは計算で求められる。
タンジェントがわかれば、サインやコサインは計算で求められる。
そのためにあるのが、三角比の相互関係の公式です。
tanθ=sinθ/cosθ
sin2θ+cos2θ=1
1+tan2θ=1/cos2θ
(2は指数として読んでください。三角関数の倍角みたいに見えて嫌なんですけど)
この公式は物凄く重要で、以後、度々登場します。
使わないと解けない問題が多数あります。
以後もずっと使い続けます。
高2の「三角関数」でも、この公式を使います。
三角比は、地道に計算で解くなどありえない単元です。
公式を使えるかどうかが全てといっても過言ではありません。
そういう意味で、公式を覚えるのが苦手な子は、「三角比から拒絶されている」という感覚を抱くことがあるようです。
「三角比」という単元を無機質に感じ、全く親しみを覚えないようなのです。
逆に公式さえ覚えれば、三角比は何でもないものなのです。
と、これくらい強調しても公式を覚えない子がいるのが高校数学の不可解なところです。
ちょっと努力しないと覚えられないような公式が多いからでしょうか。
確かに、小学校の頃の三角形の面積の公式のように楽にスルスル覚えられるものではありませんよね。
そのためか、
「まあ、今は教科書を見ながら解いて、テスト前に暗記します」
と悠長に構えている子が多いのです。
しかし、以後の問題にはこれらの公式を使います。
問題集の解答・解説は、この公式を使ったことは、いちいち解説されていません。
解説が省略されていて、何のことかわからない。
それは、公式を覚えていないことからきている場合が大半です。
公式は忘れた頃にまた使います。
「三角比」は「三角比」だけで終わる単元ではありません。
高校二年になると、「三角関数」という単元があります。
これは、「三角比」で学習した内容を前提として先に進みます。
三角比の公式を短期記憶にしかせず、全部忘れていると、翌年えらい目にあいます。
公式は、早め早めに覚えて、覚えた状態で使い、長期記憶にすることをお勧めします。
とりあえず、上の3つの公式を証明してみましょう。
まずは1本目。
tanθ=sinθ/cosθ から。
tanθ=sinθ/cosθ から。
三角比の定義より、上の図で
sinA=a/c
両辺をc倍すると、a=c・sinA
同様に、
cosA=b/c
よって、b=c・cosA
ゆえに、
tanA=a/b=c・sinA/c・cosA=sinA/cosA
次に、2本目。
sin2θ+cos2θ=1
sin2θ+cos2θ=1
これを証明します。
三平方の定理より a2+b2=c2
よって、(c・sinA)2+(c・cosA)2=c2
c2・sin2A+c2・cos2A=c2
両辺をc2で割って、
sin2A+cos2A=1
3本目はこの sin2A+cos2A=1 の両辺をcos2Aで割ります。
sin2A/cos2A+1=1/cos2A
tan2A+1=1/cos2A
なお、実際に計算する際には、上の公式の両辺を逆数にして、
cos2θ=1/(1+tan2θ)
を活用しても良いでしょう。
また、1本目の公式、tanθ=sinθ/cosθ
の両辺にcosθをかけて、
sinθ=tanθ・cosθ
と変形した式を活用すると計算が楽です。
では、実際に問題を問いてみましょう。
問題 sinθ=3/5 を満たす鋭角θの、cosθとtanθの値を求めよ。
sin2θ+cos2θ=1より
cos2θ
=1-sin2θ
=1-(3/5)2
=1-9/25
=16/25
θは鋭角なので、cosθ>0より
cosθ=4/5
cosθ>0 なんて当たり前なのになあと感じるかもしれませんが、この直後に、cosθが負の数になる場合を学習します。
だから、これは書いておく必要のある1行なんです。
数学の答案は、何を書いて何を書かないのかよくわからなくて混乱する人がいます。
数学の答案で必要なのは、なぜそのように解けるのか、その根拠を示していくこと。
数学の答案で必要なのは、なぜそのように解けるのか、その根拠を示していくこと。
今回は、2乗が16/25なのに、なぜ-4/5は答えではないのかは説明しておく必要があります。
説明の仕方は多様です。
一字一句にこだわるようなものではありません。
さて、問題に戻りましょう。
sinθは問題の通り、3/5、cosθは4/5 と出ました。
では、tanθは?
tanθ
=sinθ/cosθ
=sinθ÷cosθ
=3/5÷4/5
=3/5×5/4
=3/4
簡単ですね。
あとは練習して慣れていけば大丈夫です。





















