2025年05月09日
1次関数の利用。動点に関する問題をついに理解した中学生の話。
例えば、こんな問題。
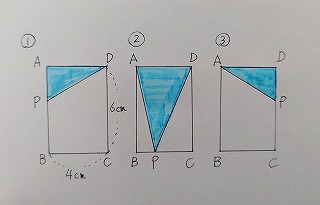
中2の「1次関数」の問題です。問題 AB=6㎝、BC=4㎝の長方形ABCDがあり、点Pは頂点Aを出発して、毎秒1㎝の速さで長方形ABCのDの辺上をB、C、Dの順に頂点Dまで動く。
点Pが頂点Aを出発してから x 秒後の△APDの面積を y ㎠として、次の問いに答えよ。
(1) 点Pが次の辺上を動く場合に分けて、y を x の式で表せ。また x の変域を示せ。
① 辺AB上
② 辺BC上
③ 辺CD上
(2) 点Pが頂点Aを出発してから12秒後の△APDの面積を求めよ。
(3) △APDの面積が10㎠になるのは、点Pが頂点Aを出発してから何秒後か。すべて求めよ。
問題には、実際には上の図①が描いてあります。
図②、③は問題には描いてなく、自分で描く必要があります。
さて、この問題は典型題です。
定期テストに出ると思って備えておいたほうがよい問題ですが、単純な計算問題とは違い、問題の「規模」が大きいので、苦手なままやり過ごしてしまう子が多いのです。
問題がスペースをとりますので、問題集に1問か2問しか載っていないこともあり、自力で解けないまま終わるのです。
何回でも自分で解き直してマスターすればいいのですが、数学が苦手な子は、そういうことはやらないのも、よくある話です。
ある生徒が中2のとき、この問題を解説演習したのですが、全く理解している様子を見せない、ということがありました。
問題文のここまではわかるか、解説のここまではわかるかと確認をとると、全部「はい」と答えていたのです。
しかし、設問に入ると、暗礁に乗り上げました。
私とのやりとりは、大体こんなふうでした。
「まず(1)の①です。
これは問題の図にある通りですね。
△APDの面積を求めましょう。
底辺をADとしましょう。
ADの長さは?」
「・・・」
「三角形が逆立ちしていると考えてください。
底辺が上にあってもいいのです。
底辺ADは、何㎝ですか」
「・・・6㎝」
「・・・何で?ADの長さですよ」
「ABに聞こえました」
「・・・ADがABに聞こえた?」
「はい」
BとDの音は、確かに聞き分けにくいのです。
だから、数学の先生の中には、Dを「デー」とあえて発音する人もいます。
テレビCMでも、タウリン1000mg配合の栄養剤の商品名は、思い切り「デー」と発音していますよね。
だから、そういう誤解は、理解できました。
「ADですよ。えー・でー」
最初から、私はADを指さしていたのでした。
「ADの長さは何㎝ですか」
「・・・」
「長方形の向かいあう辺の長さは等しいですよ?」
「・・・」
ADだと理解しても、結局、わからない・・・。
こうしたやりとりが続き、この問題を1題解くのに授業時間を全部費やすことになりました。
類題を宿題に出しましたが、勿論解いてこられるはずもありませんでした。
定期テストに類題が出ましたが、やはり、解けませんでした。
予想はしていたことでした。
基礎学力に不安のある子でしたので、こうした応用問題にそんなに時間をかけられなかったのでもあります。
まずは、直線の式の求め方などの基本問題で得点できるようにすることが優先でした。
約1年後の夏期講習でのことでした。
中3になったその子に、今度は入試対策として、上の問題を解説しました。
都立入試には、このような1次関数の文章題は出題されませんが、動点ということでいえば、大問5の空間図形に動点が出てくることがあります。
また、内申が決まる大事な2学期のテスト範囲は2次関数であることが予想され、それにも動点の問題は出題されます。
今度こそ、理解してほしい・・・。
その子を長く教えているうちに、教え方もわかってきました。
その子に教えるにしては、私の教え方はスピードが速かったのです。
話し方にも課題がありました。
「まず(1)の①です」
ここでしばらく間をおかないと、その子の気持ちがついてこないことが、わかってきました。
他の生徒なら、
「え?何の時間?」
と問い返してくるほどの長い間が必要なのでした。
「①は問題の図にある通りです」
これとかそれといった指示語は、できるだけ避けることが必要でした。
文脈がわからなくなるのです。
「△APDの面積が y です。
△APDは、三角形です。
わかりますか」
長い間の後、その子はうなずきました。
「三角形の面積を求めます。
三角形の面積の公式を、言ってください」
長い間の後、その子は答えました。
「・・・底辺×高さ÷2」
「底辺×高さ×1/2としましょう。
いいですか」
その子は、うなずきました。
「この公式に数字や文字をあてはめましょう。
底辺を、ADとします。
底辺ADの長さは何㎝ですか」
私の話し方の癖として、「底辺ADの長さは?」と済ませてしまうことが多く、実際、たいていの場合はそれで通じるのですが、それでは伝わらない子もいます。
文は、最後まで言わないと意味が伝わらないのです。
「底辺ADの長さは何㎝ですか」
この問を発した後は、先刻よりも長時間待つ必要があります。
じっくり考える時間が必要なのでした。
「底辺ADは、何㎝ですか」
「・・・6㎝」
「・・・何で?」
「ABに聞こえました」
6㎝と誤答するまでには非常に時間がかかるのに、「ABに聞こえました」という言い訳は間髪を入れずなのが、教える者を混乱させるところです。
言い訳のスピードがおそろしく速いのです。
頭の回転が速い子と、誤解するじゃないですか?
でも、そうとは限らないのです。
いや、ある意味、頭の回転は速いのでしょう。
むしろ、頭が回転しすぎて、混乱している状態なのだと、私は徐々に理解してきました。
「・・・ADが、ABに聞こえた?」
「はい」
「・・・ちょっと待って。あなたとは、1年前にも、同じ会話をしましたよ?」
「・・・」
「再放送なの、この授業は?」
あのとき、私は、ADがABに聞こえたということのリアリティーに納得したけれど、それは、本質ではなかったのではないか?
ADがABに聞こえたのは、事実だったでしょう。
しかし、私は、ずっと△APDの話をしていたのです。
底辺ADと、説明していました。
ボードに図を描き、ADを指さしていたのです。
ABは、△APDからは離れている線分です。
音が似ていても、普通、混同はしないのです。
なぜ、そこで混同するのか?
・・・この子は、全体の流れを理解していないのではないか。
私の解説の文脈が読めていないのではないか。
何か問われたら、反射的に答えているけれど、なぜそれを問われているのかは理解していないのではないか・・・。
では、なぜ、そんなことが起こるのか?
そもそも、私の話のほとんどを聞き取れていないからではないのか?
だから、聞き取れた部分だけに必死に反応して、わかっているふりをしているのではないか?
そうだとすると、では、どうすれば、解決するのだろう・・・。
私は、問題文をその子に音読してもらいました。
その後、
「今、読んだ問題文で、わからないところは、ありますか。
あったら、質問してください」
「・・・下・・・」
「下?」
「・・・下がわからない・・・」
「下とは何のことですか。
わからないところを音読してください」
「・・・点Pが頂点Aを出発してからx秒後の△APDの面積をy㎠として、次の問いに答えよ」
問題文が2行あるうちの下の行、と言いたかったのでした。
もう一度、問題文を見てみましょう。
問題 AB=6㎝、BC=4㎝の長方形ABCDがあり、点Pは頂点Aを出発して、毎秒1㎝の速さで長方形ABCDの辺上をB、C、Dの順に頂点Dまで動く。
点Pが頂点Aを出発してからx秒後の△APDの面積をy㎠として、次の問いに答えよ。
下がわからない・・・。
点Pが頂点Aを出発してからx秒後の△APDの面積をy㎠として、次の問いに答えよ、がわからない・・・。
・・・なぜだろう?
1次関数の最初の学習のときにも、このように、x と y の関係を表す式を求める問題はあり、そのときには、わからないとは言わなかったのです。
この文のどこがわからないのだろう?
いや、むしろ、わからない原因は、1文目のほうなのではないか?
「まず、1文目を見てください。
点Pは頂点Aを出発して、毎秒1㎝の速さで長方形ABCDの辺上をB、C、Dの順に頂点Dまで動く、というのは、わかりますか」
「・・・わかりません」
「・・・そうですか」
ここからが、正念場でした。
「点Pは頂点Aを出発して、毎秒1㎝の速さで長方形ABCDの辺上をB、C、Dの順に頂点Dまで動くのです。
わかりますか」
「わかりません」
「では、主語と述語だけ取り出します。
点Pは、動く。
わかりますか」
「・・・わかりません」
・・・そうか。
ああ、そうか。
文章を読んで理解するのが苦手な子は、図やグラフのある問題は、そればかり見てしまう傾向があります。
そのとき、問題にある図の点Pは止まっています。
だから、点Pが動くということを、理解していない・・・。
一方、この問題で三角形の面積を求めよと言われても、APの長さに関する情報は、図の中にはない・・・。
x は、図に全く出てこないのです。
「点Pは、動く。
点Pは、動くんです。
点Pは、実は、動くんです。
動くんです。
頭の中で、点Pを動かしてください。
動画だと思って。
アニメだと思って。
点Pは、動くんですよ」
「・・・」
待つこと1分ほど。
その子に、驚愕の表情が浮かびました。
「わかりましたか?
点Pは、動くんです」
動点の問題がわからない子の中には、点Pが動くことを問題文から読み取っていない子たちがいます。
そもそも、そんなことはあり得ないから、考えたこともない子もいます。
問題文を読解できないので、点Pが動くという情報を得ていない子もいます。
主語と述語が遠い文は、途中の大量の修飾語に阻まれて、意味を理解できないのです。
問題に書いてあるのに、読み取れない。
そして、挿絵に過ぎない図ばかりを眺めて、困惑してしまう・・・。
図の中では止まっている点P。
点Pについての情報は、図の中には何もない。
だから、x と y の関係を表す式を求めよと言われても、何のことかわからない・・・。
私の出すヒントが、どういう文脈で出されているものなのか、理解できない・・・。
なぜADの長さを訊くのか理解できないので、ABと聞き違えることも普通に起こる・・・。
「問題に描いてある図は、点Pが、辺ABの上を動いている途中を描いたものです。
点Pは、いつもここにいるわけではないのです。
辺BC上にも、いきます。
辺、CD上にも、いきます。
それぞれで、x 秒後の面積 y ㎠の求め方は変わってくるので、場合に分けて、その式を求めなさいと問題は言っているんです」
その子は、無表情のままでした。
もともと表情に乏しく、いつも、何もわかっていない顔をしているのですが、わかっていない顔でわかっているときもあり、判断が難しいのでした。
「わかりましたか」
「はい」
という会話に、あまり意味はなく、わかっていないのに「はい」と返事をすることは常態でした。
それでも、問題の意味は理解したと仮定して、進むしかありません。
「(1)の①を解きます。
点Pは、辺AB上にいます。
△APDの底辺をADと考えます。
三角形が逆立ちしているんです。
ADが底辺です」
ゆっくり、ゆっくり説明しました。
「底辺ADの長さは?」
「4㎝」
「そうです!
では、△APDの高さは何㎝ですか」
「・・・」
「高さは、APですね」
「・・・動く・・・」
「・・・はい?」
「・・・動く・・・」
その子のほうから何か反応があるのは、ありがたいことでした。
常に沈黙し、最後まで聞いて、結局、何もわからない、ということもありました。
「・・・点Pが動くから、わからない、ということですか」
「はい」
「動く長さを x を使って表すのです」
「・・・」
その子に限らず、関数の本質を理解していない中学生は、多いのです。
わかっている顔をし、基本問題だけは解きますが、関数とは何であるのか、本質は理解していません。
関数なんて何の役に立つのか、と思っているので、理解しようとする気持ちが薄い場合もあります。
関数の式なんか立てたところで、x も y も結局定まらない。
こんな無価値なものを理解しても仕方ない、と思ってしまうようです。
価値を認めていないので、理解しようというモチベーションが低い。
こんなものは理解しない自分のほうが正しいのだと思っている場合もあります。
はっきり自覚していなくても、関数についての情報をシャットアウトしがちで、関数については解説が耳に届かなくなる子たちがいます。
もう1つの課題。
これは、速さの問題でもあるのです。
点Pは、毎秒1㎝の速さで動いています。
速さの問題としては非常にわかりやすいものですが、速さの問題について小学生の頃から結局理解できていない子たちには、やはり大きな課題です。
速さ×時間=道のり
この公式の意味を実感として理解できず、速さの単元のときだけ公式を丸暗記して、テストが終わればすぐに忘れてしまった子たちは、中学数学で随所に出てくる速さの要素に対応できないことがあります。
この問題では、点Pは、点Aを出発し、毎秒1㎝の速さで動きます。
速さ×時間=道のり
速さが毎秒1㎝で、時間が1秒ならば、
1×1=1
つまり、1秒後のAPの長さは、1㎝。
同様に、2秒後には、2㎝動きます。
つまり、2秒後のAPの長さは、2㎝。
使っている公式は、
速さ×時間=道のり
今は、速さが1ですから、
1×時間=道のり
だから、x 秒後のAPの長さは、x ㎝です。
時間の数値がそのまま道のりになります。
速さの復習を行って、ようやくその理解にたどりつきました。
「APの長さは、x ㎝とわかりましたね」
「はい」
「では、△APDの面積 y ㎠を表す式は?」
「・・・」
長い沈黙がありました。
「・・・計算して何か数字を答えろと言っているのではないのですよ。
x を使って表すんです。
式は、どうなるでしょうか。
底辺ADが4㎝。高さが x ㎝の三角形の面積が y です」
長い時間待って、ようやくその子の口から出た式は、
y=4×x÷2
数学が苦手な中学生は、3年生になっても、小学校の知識が顔を出します。
アップデートできていないことがあります。
「・・・割り算は、もうやめましょう。
自分で計算を難しくするだけです。
÷2は、×1/2に直せます。
三角形の面積の公式は、底辺×高さ×1/2です」
「はい」
y=4×x×1/2
これを整理すると。
y=2x
ようやく、正解にたどりつきました。
それでは、次に x の変域を求めます」
「・・・」
変域のこともその子は忘れていたので、復習が必要でした。
「最初に点Pはどこにいたのでしょう。x はいくつですか」
「1」
「1から始まると思うのは、やめてください。
0から始まるのです」
「・・・」
数学が苦手な子は、なぜか共通の発想をもっていることが多いです。
数字は1から始まると思っています。
数に対する感覚が自然数なのです。
数は、必ず1から始まることになっているようです。
0と言われれば理解できるのですが、自力では発想できないことがあります。
「では、点Pが、点Bの位置に来たとき、x はいくつですか」
「・・・」
また速さの問題です。
毎秒1㎝の速さですから、本当はすごく簡単なのですが、速さが苦手な子にとっては、難問です。
道のり÷速さ=時間
点Pが点Bの位置に来たときの道のりは、AB=6㎝。
速さは、毎秒1㎝。
6÷1=6
点Pが点Bに来るのは、6秒後です。
・・・そんなの見ればわかるじゃないか。
毎秒1㎝の速さならば、時間と道のりが同じ数字なんだから。
しかし、見てもわからないのが、数学が苦手ということの実態です。
速さの3公式に対して実感がないので、いちいち公式にあてはめないと、わからないのです。
ここを省略すると、わからないままで終わります。
時間が x 秒のとき、道のりが同じ x ㎝になる理由がわからないので、混乱するのです。
ともかく、(1)の①は、できました。
y=2x (0≦x≦6)
が答えです。
何とかここまでくると、②は順調でした。
点Pが、辺BC上を動いている間は、△APDの面積は一定。
そのことは、比較的すんなり理解できました。
底辺AD=4㎝
その底辺から見た高さは、常に辺ABの長さと同じ6㎝です。
よって、面積は、
y=4×6×1/2
y=12
変域は、
点Pが点Bにいるときは6秒後。
点Pが点Cにいるのは、6+4=10(秒後)ですから、
6≦x≦10
さて、③です。
これは、数学がある程度まで理解できる子も、自力では解けないまま終わってしまうことのある問題です。
考え方が少しだけ難しいのです。
点Pが辺CD上にあるときの△APDの面積。
底辺はやはりAD=4㎝
では、高さは?
高さは③の図のDPです。
これは、x でしょうか?
違いますよね。
では、どう表しましょうか。
これが、難しいのです。
「引き算の発想をしましょう。
全体の道のりから、要らない部分を引くと、DPの長さを求めることができます。
点Pは、点Aを出発して、点Bの角を曲がり、さらに点C角を曲がって、今、辺CD上にいます。
そこまでの道のりが、x ㎝です。
DPは、残りの道のりです。
何マイナス何をすればいいでしょうか?」
図で指さしながら、点Pのたどる道のりを何度も示しました。
長い沈黙の後、その子は答えました。
「20-x」
「20?」
私が問い返すと、不安になったようで、
「10-x」
「10?」
「6-x」
「・・・いや、答を連発するのはやめて、よく考えてください。全部不正解ですよ」
「20-x」
・・・いかん。
その場しのぎの即答モードに入ってしまったのでした。
私の問うことに何か反射的に答えることで、わかっているふりをするのです。
何も答えないか、何かを即答するか。
そして、何かを即答しているときのほうが、実は混乱しているのです。
「・・・即答しなくていいから、よく考えて。どんな式で20という数字が出たのですか?」
「6+4+6+4」
「・・・それは、長方形の周の長さですね。
DAの長さは必要ないです。
点Pは、辺DAは通りません」
「・・・」
点Pは、Aから出発し、Bを曲がってCを曲がってDに到達して止まります。
それは、問題に書いてあります。
しかし、こういう「規模」の大きい問題を解いた経験のあまりない子は、解いているうちに問題の条件を忘れてしまいます。
全体ならば、長方形の周の長さ。
そういう、昔、どこかで使った知識の記憶が頭を横切って、それを使ってしまうのだと思います。
Dまでの全体の道のりは、
AB+BC+CD
=6+4+6
=16
です。
その全体の道のりの中で、今、点Pは、CDの途中まで来ています。
毎秒1㎝の速さで、x 秒進んできました。
その道のりは、
1×x=x
その道のりを引けば、残りの道のりDPの長さがわかります。
DP=16-x
です。
悲しいことに、この話が長引けば長引くほど、何のためにDPを求めていたのかわからなくなります。
△APDの面積を求めようとしていた、ということを忘れてしまうのです。
「それでは、△APDの面積、y を表す式を言ってください」
「y=16-x」
「いや、それは、DPの長さです」
・・・やばい。
混乱がきた!
表情から、パニックが起こりかけているのがわかりました。
「y=ax+b」
「・・・いや、その話はしていないです」
「y=16-x」
「・・・落ち着きましょう」
ゆっくり説明しないと、高さDP=16-x が理解できない。
しかし、それに時間がかかると、何のためにそれを求めていたのか忘れてしまい、戻れない・・・。
そこで最初から問題を見直していると、今度は、DP=16-x がなぜそう表せるのか、忘れてしまう。
図に書き込んであるのに、忘れてしまって、不安になって、使えない・・・。
もともと、DPを x を使って表す発想は、そのときは理解できても、またすぐ忘れてしまう子も多いです。
③の問題を自力で解けるようになるには、深い理解が必要です。
さらに、この後も、また1つ壁がありました。
三角形の面積で、最初に1/2を書く習慣がある子は大丈夫なのです。
中学数学では、三角形の面積の公式は、
1/2×底辺×高さ
です。
しかし、小学校の公式の印象が強すぎる子は、
底辺×高さ×1/2
に直すだけでも大変で、その順番までは変えられない子が大半です。
私も、そこまでは強く要求できません。
中学の公式通りに、
y=1/2×4×(16-x)
という式を立てていれば、それを整理するときミスは少ない。
しかし、上のように、最後に×1/2を書く習慣のある子は、この式をうまく展開できないことがあります。
y=4×(16-x)×1/2
=64-1/2x
としてしまう子は、数学の成績が5段階で「3」の子に、ざらにいます。
四則演算と( )の関係の理解は、永遠の課題です。
そのことを心配して、私は解説しました。
「( )を開くのは、最後にしましょう。
まず( )の外側をかけます。
4×1/2を先に計算します。
わかりますか」
「わかりません」
「何がわかりませんか」
「・・・外側」
「( )の外側です。4と1/2のことです」
その子は、首を傾げていました。
・・・自分は「下」なんて意味不明の言い方を唐突にしたくせに、「( )の外側、4と1/2」と具体的に説明していることの何がわからないんだろう・・・。
頭を抱えたくなりますが、言語体系が違うのです。
主観が強く、自分の言葉は万能だと思っているが、他人の言葉は理解しづらい。
それは、程度こそあれ、誰でもそうです。
私もそうかもしれません。
怒っても仕方ありません。
「とにかく、y=4×(16-x)×1/2 を計算してください」
諦めて、間違ったら直そうと思っていると、
「できました」
「はい。整理した式を言ってください」
「y=32-2x」
・・・何でできるんだろう・・・。
できることとできないこととの違いが、いつになっても、よくわからない・・・。
学力の安定している子なら、この子はこれならできるだろう、これは難しいだろうと把握できるのですが、簡単なことが全く理解できないのに、こういうことはするっとやり遂げたりします。
日によって、それは違うこともあります。
「y=32-2x で、そこまでは合っています。次に、1次関数らしく項の順番を整えましょう。x を含む項が先です」
「y=2x-32」
「・・・なんで?」
何で、これは出来ないのだろう・・・。
数学が苦手な子の足元に広がる深淵は、暗く深い・・・。
彼らを飲み込む深淵はそこら中に口を開けています。
中学3年生になっても、マイナスを「引き算の計算記号」としか認識できない子は多く、符号ごと項を移動するということが上手くできないことがあります。
日によっては、1次方程式の移項もすべて符号ミスをすることがあるのですが、できる日もあるのです。
安定しない・・・。
ともあれ、③の正解は、
y=-2x+36 (10≦x≦16)
です。
すべてが上手くいくわけではありません。
ミスの原因はそこら中にあります。
この問題を自力で正解できるようになるには、大変な努力が必要です。
テスト前に、やり方だけ丸暗記してやり過ごし、見た目は正解する子もいるでしょう。
しかし、時間が経てば、またわからなくなってしまうことが多いのです。
それでも、その子は、「点Pは動く」ということは、理解しました。
それは、大きな一歩でした。
そのことについては、わかっているふりから脱却したのでした。
そして、宿題に出した類題は、やはり細かいミスはあったのですが、点Pは動く、ということだけは理解した答案を書いてきました。
数週間後、都立入試の過去問を解いたときのこと。
空間図形の問題で動Pが四角錐の辺上を動く問題が出題されていました。
その子は、動点Pに関する問題は、正解できました。
まるで、それまでのつまずきなど、存在しなかったかのように。
以後も、動点についての根本的な誤解は、消え失せたのでした。
Posted by セギ at 12:01│Comments(0)
│算数・数学
※このブログではブログの持ち主が承認した後、コメントが反映される設定です。



























