2022年09月29日
都立野川公園のヒガンバナ。2022年9月。

2022年9月28日(水)、自転車で都立野川公園に行きました。
武蔵境通りをひたすら南に走り、東八道路で右折。
またひたすら走っていくと、都立野川公園です。
都立野川公園の自然観察園の前で自転車を停めて、中へ。
平日ですが、それなりに人がいます。
やはり、花の季節は人気がありますね。
普段はむしろ花は少ない自然観察園の西側の一画が、ヒガンバナの群落のある場所。
入口からも、もう赤いじゅうたんが見えていました。
やはり、まずそこが気になるので、とことこと歩いていきました。
もう最盛期は過ぎ、色はややさめているのだと思いますが、それでもこれだけ集まると見ごたえがありました。
パシャパシャと撮影。
上の画像がその1枚です。
気持ちも落ち着いたので、いつもの東側へと木道を歩いていきました。
早速見つけたのが、キバナアキギリの群落。
正直、山にはこんな群落はありません。
ぽつぽつと咲いているのを見つけると嬉しいのがキバナアキギリ。
小さいバナナが3つ集まったような、黄色い不思議な花です。
山は、鹿が食べちゃうから、本当に、花が少ないです。
こうした公園のほうが、大群落を見ることができます。
そういう意味ではいいんだけど、でも、やはり山で見たいなあ。
シュウカイドウのピンク色の花。
ヤブミョウガの黒い実。
キツリフネも咲いていました。
赤いツリフネソウも。
ヤブラン。
知らない花は、グーグルレンズで調べます。
小さな紫色の花は、カリガネソウ。
野川公園にときどきやってくるようになってもうすぐ2年になるのですが、こんなに秋の花が咲いているのを見るのは初めてです。
なんでかなあと思ったら、去年の今頃は、コロナ感染者が劇的に減ったので、山を歩いていたんですよね。
久しぶりに高尾山にいったのが、ちょうど1年前でした。
あの時期、東京都の感染者が1日で100人台まで下がっていました。
今は下がったといっても、1日5000人。
コロナウィルスが発見された初期の頃だったら、戦慄する数字です。
これで収束している感覚があるのだから、慣れとは恐ろしいものです。
うちの塾でも、濃厚接触者や陽性になったため欠席という連絡がたまに入るようになりました。
学校で文化祭をやれば、外部の見学者も多いので、それは当然そういうことに帰結します。
けれども、いつまでも学校行事を全面中止というのも、では、いつになったらこれは終わるのか?
もともと塾は週に1度の授業で、文化祭などコロナ感染の契機となったのだろう学校行事の前は、その準備を理由に生徒が授業を振り替えていました。
私がその生徒と接触したのは10日以上前の場合ばかりで濃厚接触者の範囲に含まれることはなく、相変わらずせっせと机やドアを除菌し教室を換気して、日々無事に過ごしています。
隔離期間を終えて、無事に塾にやって来た子の授業中の反応が今1つなのは、単なる文化祭ボケなのか、コロナの後遺症なのか?
ただの文化祭ボケでしょう。
そうであってほしい。
後遺症は、脳に霧がかかったようになり思考力が甚だしく衰える場合があるとの情報もあります。
やはり、コロナは感染しないほうがいいのです。
私1人のことなら、ええい、行っちゃえーと山に行くこともあるかと思います。
そもそも、山に行くことそのものがリスクの高い行為で、いつ落ちるかわからない崖っぷちなんか歩かないほうがいいに決まっています。
でも、それは私1人のこと。
コロナは、生徒に感染させます。
生徒に感染させる可能性を考えれば、用心に用心を重ねたほうがいい。
最後までマスクと除菌にこだわる人になろうと思います。
さて、都立野川公園を出て、野川沿いの遊歩道を自転車で進み、深大寺に向かいました。
お目当ては、神代植物公園水生植物園。
ここは年間を通して無料開放されています。
入口から入ってすぐのところに自転車を置いて、さてとことこと木段を降りていくと、ここも、遠くに赤いじゅうたんが見えました。
水田があり、稲穂が実って、鳥よけの網が張られています。
その周りに、ヒガンバナが咲いていました。
ここでも、パシャパシャと撮影。
さて、城址のほうに行ってみようと樹木に覆われて鬱蒼とした木段を上っていったら、侵入禁止となっていました。
そしてスズメバチの看板。
完全に侵入禁止とするほどの巨大な巣でもできているのでしょうか。
恐ろしいことである。
いったん入口付近に戻り、そこから舗装された坂道を登って、城址へ。
途中の細道に、やはり進入禁止の黄色いテープが張られてあり、スズメバチの表示がありました。
城址には登っていくことができました。
ソバ畑。
大きなフヨウの木が2本。
白い花とピンクの花。
前に来たときは、小学生の遠足で大騒ぎでしたが、今日は人影もまばらな静かな城址でした。
気温は25度。
こんなに長く自転車を走らせても、平気な気温になってきました。
秋が来ています。
山は、東京の感染者が1日1000人を切ったら、行ってみようかなあ?
そんな日は、果たして来るのかという気もしますが、とりあえず、1000人。
武蔵境通りをひたすら南に走り、東八道路で右折。
またひたすら走っていくと、都立野川公園です。
都立野川公園の自然観察園の前で自転車を停めて、中へ。
平日ですが、それなりに人がいます。
やはり、花の季節は人気がありますね。
普段はむしろ花は少ない自然観察園の西側の一画が、ヒガンバナの群落のある場所。
入口からも、もう赤いじゅうたんが見えていました。
やはり、まずそこが気になるので、とことこと歩いていきました。
もう最盛期は過ぎ、色はややさめているのだと思いますが、それでもこれだけ集まると見ごたえがありました。
パシャパシャと撮影。
上の画像がその1枚です。
気持ちも落ち着いたので、いつもの東側へと木道を歩いていきました。
早速見つけたのが、キバナアキギリの群落。
正直、山にはこんな群落はありません。
ぽつぽつと咲いているのを見つけると嬉しいのがキバナアキギリ。
小さいバナナが3つ集まったような、黄色い不思議な花です。
山は、鹿が食べちゃうから、本当に、花が少ないです。
こうした公園のほうが、大群落を見ることができます。
そういう意味ではいいんだけど、でも、やはり山で見たいなあ。
シュウカイドウのピンク色の花。
ヤブミョウガの黒い実。
キツリフネも咲いていました。
赤いツリフネソウも。
ヤブラン。
知らない花は、グーグルレンズで調べます。
小さな紫色の花は、カリガネソウ。
野川公園にときどきやってくるようになってもうすぐ2年になるのですが、こんなに秋の花が咲いているのを見るのは初めてです。
なんでかなあと思ったら、去年の今頃は、コロナ感染者が劇的に減ったので、山を歩いていたんですよね。
久しぶりに高尾山にいったのが、ちょうど1年前でした。
あの時期、東京都の感染者が1日で100人台まで下がっていました。
今は下がったといっても、1日5000人。
コロナウィルスが発見された初期の頃だったら、戦慄する数字です。
これで収束している感覚があるのだから、慣れとは恐ろしいものです。
うちの塾でも、濃厚接触者や陽性になったため欠席という連絡がたまに入るようになりました。
学校で文化祭をやれば、外部の見学者も多いので、それは当然そういうことに帰結します。
けれども、いつまでも学校行事を全面中止というのも、では、いつになったらこれは終わるのか?
もともと塾は週に1度の授業で、文化祭などコロナ感染の契機となったのだろう学校行事の前は、その準備を理由に生徒が授業を振り替えていました。
私がその生徒と接触したのは10日以上前の場合ばかりで濃厚接触者の範囲に含まれることはなく、相変わらずせっせと机やドアを除菌し教室を換気して、日々無事に過ごしています。
隔離期間を終えて、無事に塾にやって来た子の授業中の反応が今1つなのは、単なる文化祭ボケなのか、コロナの後遺症なのか?
ただの文化祭ボケでしょう。
そうであってほしい。
後遺症は、脳に霧がかかったようになり思考力が甚だしく衰える場合があるとの情報もあります。
やはり、コロナは感染しないほうがいいのです。
私1人のことなら、ええい、行っちゃえーと山に行くこともあるかと思います。
そもそも、山に行くことそのものがリスクの高い行為で、いつ落ちるかわからない崖っぷちなんか歩かないほうがいいに決まっています。
でも、それは私1人のこと。
コロナは、生徒に感染させます。
生徒に感染させる可能性を考えれば、用心に用心を重ねたほうがいい。
最後までマスクと除菌にこだわる人になろうと思います。
さて、都立野川公園を出て、野川沿いの遊歩道を自転車で進み、深大寺に向かいました。
お目当ては、神代植物公園水生植物園。
ここは年間を通して無料開放されています。
入口から入ってすぐのところに自転車を置いて、さてとことこと木段を降りていくと、ここも、遠くに赤いじゅうたんが見えました。
水田があり、稲穂が実って、鳥よけの網が張られています。
その周りに、ヒガンバナが咲いていました。
ここでも、パシャパシャと撮影。
さて、城址のほうに行ってみようと樹木に覆われて鬱蒼とした木段を上っていったら、侵入禁止となっていました。
そしてスズメバチの看板。
完全に侵入禁止とするほどの巨大な巣でもできているのでしょうか。
恐ろしいことである。
いったん入口付近に戻り、そこから舗装された坂道を登って、城址へ。
途中の細道に、やはり進入禁止の黄色いテープが張られてあり、スズメバチの表示がありました。
城址には登っていくことができました。
ソバ畑。
大きなフヨウの木が2本。
白い花とピンクの花。
前に来たときは、小学生の遠足で大騒ぎでしたが、今日は人影もまばらな静かな城址でした。
気温は25度。
こんなに長く自転車を走らせても、平気な気温になってきました。
秋が来ています。
山は、東京の感染者が1日1000人を切ったら、行ってみようかなあ?
そんな日は、果たして来るのかという気もしますが、とりあえず、1000人。
2022年09月23日
三角方程式の難問。

問題 0≦x<π/2 のとき、
1+cos x-sin x-tan x=0 を解け。
難問というほどのことはないと感じる人もいるかもしれませんが、はまってしまうと意外と厄介なのがこうした問題です。
これは三角方程式。
このタイプの問題は、cosの2乗の項かsinの2乗の項が1つ含まれていることが多く、そこからどう解くのか見えるのですが、すべての項が1乗で、しかも、サイン、コサイン、タンジェントがそろっています。
こういうのっぺりした、とっつきにくい問題は、解きにくいですね。
どこから手をつけましょうか?
三角方程式は、すべてサインか、すべてコサインに揃えてしまえば、あとは簡単です。
何に揃えましょうか。
とりあえず、タンジェントだけでも、まずは消しましょうか。
tan x=sin x / cos x ですから、それを代入して、
1+cos x-sin x-sin x / cos x=0
うーん。
分母のコサインが邪魔なので、式全体に cos x をかけてみます。
cos x+cos^2 x-sinx・cosx -sin x=0
ほお?
これは、いい調子。
これは、因数分解できますよね?
ここまで、闇雲にやってきてしまいましたが、ここで道筋が見えました。
何をやっているかわかりやすいように、項の順番をまず変えて書いてみます。
cos^2 x-sinx・cosx +cos x-sin x=0
前2つの項を共通因数でくくります。
ついでに、後ろ2つも( )でくくっておきます。
cos x(cos x-sin x)+(cos x-sin x)=0
( )の中身が同じになりました。
これが新しい共通因数です。
(cos x-sin x)(cos x+1)=0
いけました。
さて、これからどうするか?
中3で学習した2次方程式の計算のときもそうでしたが、積が0ならば、少なくともどちらか一方は0です。
0に何をかけても0。
逆にいえば、答が0になっているときは、少なくともどちらか一方は0です。
例えば、
(x-1)(x+3)=0
という2次方程式ならば、
x-1=0、または、x+3=0 であり、そこから、
x=1 , x=-3
という2つの解を導くのでした。
この因数分解による解き方は、作業手順だけ覚えて、なぜそのように解けるのかわからなくなる中3が多いところです。
定期テストでその根本を問われると、意味を理解している子以外は全滅してしまう嫌なところです。
繰り返しこのブログに書いていることですが、小学生の頃から何でも作業手順の暗記で済ませてしまい、結局、意味が後退し消失している子は多いです。
だから、高校数学で、以前学習した考え方を応用できないのです。
意味を理解しましょうとどれだけ促しても、小学生の頃からの学習の癖はなかなか消し難く、何でもすぐ作業手順に変えてしまいます。
それはともかく、元の問題に戻りましょう。
(cos x-sin x)(cos x+1)=0
ということは、
cos x-sin x=0
または、
cos x+1=0 です。
ところで、これは、両方の式が成り立つのでしょうか?
ここで、x の定義域が生きてきます。
多くの問題が、0≦x<2π といった、大抵の生徒がそれ以外のことなどそもそも考えていない定義域であるため、問題文のこうしたところをろくに読まない子がいますが、今回の定義域はそれではありませんでした。
0≦x<π/2
という、いつもと違う狭い定義域でした。
単位円を描いて考えれば、これは、第1象限の角ということです。
随分狭い。
それには、意味があるはずです。
0≦x<π/2 のとき、コサインの値は、正の数です。
負の数にはなりません。
(【注】今の話がそもそもわからないという場合は、数Ⅰ「三角比」の復習が必要です。回り道のようで、それが近道です)
すなわち、0≦x<π/2 より、
0<cos x≦1
よって、
cos x+1≠0
ということは、
cos x-sin x=0
または、
cos x+1=0
と先ほど考えましたが、2本目の可能性は消えました。
よって、
cos x-sin x=0
はい、もらった、この問題!
もうこの先は、見えた!
と喜ぶ人は、「三角関数」の基本はよく身についている人だと思います。
しかし、定期テストの前日に必死に公式を暗記してやり過ごし、テストが終われば記憶をすべて消去してしまうタイプの人は、ここで、行き詰まります。
「数学の単位だけがほしい。数学は嫌い。受験に数学は使わない」
というのであれば、それも仕方ないと思うのですが、受験に数ⅡBを使う予定があるのに、それでもそんな勉強のやり方をするのは本当にやめたほうがいいのです。
受験勉強をしようという時期に、数ⅡBを基礎からやり直し。
入試問題を解けるレベルにはなかなか到達しません。
昔は、数ⅡBを学習した時点で、あ、こりゃダメだ、理系は無理だ、文系に行こう、と判断する生徒が大多数でした。
今は、そういう観点で文系・理系を選択するとは限りません。
「地歴公民の暗記ができない」
「古文・漢文が死ぬほど嫌い」
「理数も嫌いだけど、就職を考えたら、経済学部か理系の学部のほうが、いいのかなあ」
といった理由で数ⅡBを入試に利用しようとする子が増えてきたように感じます。
その判断基準は、ちょっと変です。
でも、1人だけ変なのではなく、そういう人が多くなれば、また状況は変わってきます。
そもそも、将来について現実的に考えている子は、高校の定期テストでしっかり得点し内申をがっちり固めて、学校推薦ないしは総合型選抜で大学に合格していきます。
いまや過半数が推薦または総合型選抜の時代。
そうした中で、一般選抜の入学試験を受けて大学に行こうとするのは、国立大学などを目指す本当に学力も意識も高い子か、将来を何も考えていなかったためにそういう羽目に陥ってしまった子たちです。
内申が悪いので、総合型選抜を受けられない・・・。
そして、「内申が悪いので、総合型選抜を受けられない」と「地歴公民の暗記ができないので理系に進みます」には、同じ匂いを感じるんです。
嘆いてばかりいる必要はありません。
国立大学などを目指す本当に学力も意識も高い子たちと競いあうわけではないからです。
秀才たちの激戦、空中戦は、「凄いな、あれ」と見上げるだけで関わらなければいい。
内申が悪いので総合型選抜を受けられない子たちには、その子たちの闘いがあります。
つまり、同じ大学を目指すライバルたちも、別にそんなに理数系が得意なわけではない、ということ。
昔と比べて理系の偏差値が何だか低い理由の1つはこれなのかもしれません。
同学年全体の人数も少ない。
何とかなります。
頑張りましょう。
cos x-sin x=0
さて、どうしましょうか?
第1象限でサインとコサインの値が同じ?
それは、きっと、x=π / 4
答だけ書けばいい問題ならそれで良いのですが、記述答案となると、そこをしっかり示さなくては。
どうやって?
基礎が身についている人にとっては、簡単です。
サインとコサインだけになったら、三角関数の合成で、サインだけにできます。
三角関数の合成。
数ⅡBが苦手な子は「三角関数」の公式をほとんど覚えていません。
それでも、加法定理はかすかに覚えていたりします。
「咲かないコスモス、コスモス咲かない、とかいうやつ?」
「・・・それは、どの加法定理のことですか?」
と、聞いていて憮然としたりすることはありますが、何となく、そんなの覚えたなあという記憶は本人にあるようです。
2倍角の公式も、覚えてはいないけれど、そんなのがあったという記憶はある子が多いです。
しかし、三角関数の合成は、記憶が欠落している子が大多数です。
もうそこらへんは公式まみれで、三角関数は捨てるしかなくなり、諦めてしまった結果なのかもしれません。
「学校で習っていない」
と言い出す子もたまにいますが、これを学習しない学校はありません。
発展的学習ではないからです。
これは、三角関数の基本です。
a sinΘ+b cosΘ=√a^2+b^2・sin(Θ+α)
これが、三角関数の合成の公式。
加法定理の、
sin(α+β)=sin α・cosβ + cosα・sinβ
の左辺と右辺を入れ替えて、
sin α・cosβ + cosα・sinβ=sin(α+β)
という形で活用している公式です。
ここで、sin(Θ+α) を計算で求める方法もありますし、それが基本ですが、もっと簡単に α を特定することもできます。
a sinΘ+b cosΘ の a と b をそれぞれ x座標、y座標とする点P(a , b)を座標平面にとり、原点Oと結んで、線分OPを描きます。
その線分OPと、x軸の正の方向との成す角が、α になります。
このブログでは読みにくいので、証明はここでは省略します。
興味があったら、参考書などを見てください。
しかし、学校で学習した記憶のない子の場合、証明を省略すると、そこで凝固してしまい、全く先に進めないことがあります。
説明を聞けば、そんなものは重視せず、いつものように作業手順だけ覚えて済ます子たちが、説明を省略されると不安になるようです。
不思議なものです。
そうしたことで揺さぶりをかけ、意味に戻ることの大切さに気づいもらいたい。
共通テストは、意味に戻れないと解けない問題が多いですから。
それでは、三角関数の合成で解いてみましょう。
cos x-sin x=0
すなわち、
-sin x+cos x=0
三角関数の合成により、
√2・sin(x+3/4π)=0
両辺を√2でわって、
sin(x+3/4π)=0
これはサインの値が0ということですから、頭の中で単位円をイメージして、
x+3/4π=0 , π
よって、
x=-3/4π、1/4π
ここでまた、最初の定義域に戻ります。
0≦x<π/2 より、
x=1/4π
これが答です。
1+cos x-sin x-tan x=0 を解け。
難問というほどのことはないと感じる人もいるかもしれませんが、はまってしまうと意外と厄介なのがこうした問題です。
これは三角方程式。
このタイプの問題は、cosの2乗の項かsinの2乗の項が1つ含まれていることが多く、そこからどう解くのか見えるのですが、すべての項が1乗で、しかも、サイン、コサイン、タンジェントがそろっています。
こういうのっぺりした、とっつきにくい問題は、解きにくいですね。
どこから手をつけましょうか?
三角方程式は、すべてサインか、すべてコサインに揃えてしまえば、あとは簡単です。
何に揃えましょうか。
とりあえず、タンジェントだけでも、まずは消しましょうか。
tan x=sin x / cos x ですから、それを代入して、
1+cos x-sin x-sin x / cos x=0
うーん。
分母のコサインが邪魔なので、式全体に cos x をかけてみます。
cos x+cos^2 x-sinx・cosx -sin x=0
ほお?
これは、いい調子。
これは、因数分解できますよね?
ここまで、闇雲にやってきてしまいましたが、ここで道筋が見えました。
何をやっているかわかりやすいように、項の順番をまず変えて書いてみます。
cos^2 x-sinx・cosx +cos x-sin x=0
前2つの項を共通因数でくくります。
ついでに、後ろ2つも( )でくくっておきます。
cos x(cos x-sin x)+(cos x-sin x)=0
( )の中身が同じになりました。
これが新しい共通因数です。
(cos x-sin x)(cos x+1)=0
いけました。
さて、これからどうするか?
中3で学習した2次方程式の計算のときもそうでしたが、積が0ならば、少なくともどちらか一方は0です。
0に何をかけても0。
逆にいえば、答が0になっているときは、少なくともどちらか一方は0です。
例えば、
(x-1)(x+3)=0
という2次方程式ならば、
x-1=0、または、x+3=0 であり、そこから、
x=1 , x=-3
という2つの解を導くのでした。
この因数分解による解き方は、作業手順だけ覚えて、なぜそのように解けるのかわからなくなる中3が多いところです。
定期テストでその根本を問われると、意味を理解している子以外は全滅してしまう嫌なところです。
繰り返しこのブログに書いていることですが、小学生の頃から何でも作業手順の暗記で済ませてしまい、結局、意味が後退し消失している子は多いです。
だから、高校数学で、以前学習した考え方を応用できないのです。
意味を理解しましょうとどれだけ促しても、小学生の頃からの学習の癖はなかなか消し難く、何でもすぐ作業手順に変えてしまいます。
それはともかく、元の問題に戻りましょう。
(cos x-sin x)(cos x+1)=0
ということは、
cos x-sin x=0
または、
cos x+1=0 です。
ところで、これは、両方の式が成り立つのでしょうか?
ここで、x の定義域が生きてきます。
多くの問題が、0≦x<2π といった、大抵の生徒がそれ以外のことなどそもそも考えていない定義域であるため、問題文のこうしたところをろくに読まない子がいますが、今回の定義域はそれではありませんでした。
0≦x<π/2
という、いつもと違う狭い定義域でした。
単位円を描いて考えれば、これは、第1象限の角ということです。
随分狭い。
それには、意味があるはずです。
0≦x<π/2 のとき、コサインの値は、正の数です。
負の数にはなりません。
(【注】今の話がそもそもわからないという場合は、数Ⅰ「三角比」の復習が必要です。回り道のようで、それが近道です)
すなわち、0≦x<π/2 より、
0<cos x≦1
よって、
cos x+1≠0
ということは、
cos x-sin x=0
または、
cos x+1=0
と先ほど考えましたが、2本目の可能性は消えました。
よって、
cos x-sin x=0
はい、もらった、この問題!
もうこの先は、見えた!
と喜ぶ人は、「三角関数」の基本はよく身についている人だと思います。
しかし、定期テストの前日に必死に公式を暗記してやり過ごし、テストが終われば記憶をすべて消去してしまうタイプの人は、ここで、行き詰まります。
「数学の単位だけがほしい。数学は嫌い。受験に数学は使わない」
というのであれば、それも仕方ないと思うのですが、受験に数ⅡBを使う予定があるのに、それでもそんな勉強のやり方をするのは本当にやめたほうがいいのです。
受験勉強をしようという時期に、数ⅡBを基礎からやり直し。
入試問題を解けるレベルにはなかなか到達しません。
昔は、数ⅡBを学習した時点で、あ、こりゃダメだ、理系は無理だ、文系に行こう、と判断する生徒が大多数でした。
今は、そういう観点で文系・理系を選択するとは限りません。
「地歴公民の暗記ができない」
「古文・漢文が死ぬほど嫌い」
「理数も嫌いだけど、就職を考えたら、経済学部か理系の学部のほうが、いいのかなあ」
といった理由で数ⅡBを入試に利用しようとする子が増えてきたように感じます。
その判断基準は、ちょっと変です。
でも、1人だけ変なのではなく、そういう人が多くなれば、また状況は変わってきます。
そもそも、将来について現実的に考えている子は、高校の定期テストでしっかり得点し内申をがっちり固めて、学校推薦ないしは総合型選抜で大学に合格していきます。
いまや過半数が推薦または総合型選抜の時代。
そうした中で、一般選抜の入学試験を受けて大学に行こうとするのは、国立大学などを目指す本当に学力も意識も高い子か、将来を何も考えていなかったためにそういう羽目に陥ってしまった子たちです。
内申が悪いので、総合型選抜を受けられない・・・。
そして、「内申が悪いので、総合型選抜を受けられない」と「地歴公民の暗記ができないので理系に進みます」には、同じ匂いを感じるんです。
嘆いてばかりいる必要はありません。
国立大学などを目指す本当に学力も意識も高い子たちと競いあうわけではないからです。
秀才たちの激戦、空中戦は、「凄いな、あれ」と見上げるだけで関わらなければいい。
内申が悪いので総合型選抜を受けられない子たちには、その子たちの闘いがあります。
つまり、同じ大学を目指すライバルたちも、別にそんなに理数系が得意なわけではない、ということ。
昔と比べて理系の偏差値が何だか低い理由の1つはこれなのかもしれません。
同学年全体の人数も少ない。
何とかなります。
頑張りましょう。
cos x-sin x=0
さて、どうしましょうか?
第1象限でサインとコサインの値が同じ?
それは、きっと、x=π / 4
答だけ書けばいい問題ならそれで良いのですが、記述答案となると、そこをしっかり示さなくては。
どうやって?
基礎が身についている人にとっては、簡単です。
サインとコサインだけになったら、三角関数の合成で、サインだけにできます。
三角関数の合成。
数ⅡBが苦手な子は「三角関数」の公式をほとんど覚えていません。
それでも、加法定理はかすかに覚えていたりします。
「咲かないコスモス、コスモス咲かない、とかいうやつ?」
「・・・それは、どの加法定理のことですか?」
と、聞いていて憮然としたりすることはありますが、何となく、そんなの覚えたなあという記憶は本人にあるようです。
2倍角の公式も、覚えてはいないけれど、そんなのがあったという記憶はある子が多いです。
しかし、三角関数の合成は、記憶が欠落している子が大多数です。
もうそこらへんは公式まみれで、三角関数は捨てるしかなくなり、諦めてしまった結果なのかもしれません。
「学校で習っていない」
と言い出す子もたまにいますが、これを学習しない学校はありません。
発展的学習ではないからです。
これは、三角関数の基本です。
a sinΘ+b cosΘ=√a^2+b^2・sin(Θ+α)
これが、三角関数の合成の公式。
加法定理の、
sin(α+β)=sin α・cosβ + cosα・sinβ
の左辺と右辺を入れ替えて、
sin α・cosβ + cosα・sinβ=sin(α+β)
という形で活用している公式です。
ここで、sin(Θ+α) を計算で求める方法もありますし、それが基本ですが、もっと簡単に α を特定することもできます。
a sinΘ+b cosΘ の a と b をそれぞれ x座標、y座標とする点P(a , b)を座標平面にとり、原点Oと結んで、線分OPを描きます。
その線分OPと、x軸の正の方向との成す角が、α になります。
このブログでは読みにくいので、証明はここでは省略します。
興味があったら、参考書などを見てください。
しかし、学校で学習した記憶のない子の場合、証明を省略すると、そこで凝固してしまい、全く先に進めないことがあります。
説明を聞けば、そんなものは重視せず、いつものように作業手順だけ覚えて済ます子たちが、説明を省略されると不安になるようです。
不思議なものです。
そうしたことで揺さぶりをかけ、意味に戻ることの大切さに気づいもらいたい。
共通テストは、意味に戻れないと解けない問題が多いですから。
それでは、三角関数の合成で解いてみましょう。
cos x-sin x=0
すなわち、
-sin x+cos x=0
三角関数の合成により、
√2・sin(x+3/4π)=0
両辺を√2でわって、
sin(x+3/4π)=0
これはサインの値が0ということですから、頭の中で単位円をイメージして、
x+3/4π=0 , π
よって、
x=-3/4π、1/4π
ここでまた、最初の定義域に戻ります。
0≦x<π/2 より、
x=1/4π
これが答です。
2022年09月20日
助動詞+have+過去分詞 と使いまわしのきく知識。

助動詞+have +過去分詞 は、高校で学習する「助動詞」という単元の中でも出題頻度の高い文法事項です。
基本的な助動詞は、「許可・義務」系の意味と「推量」系の意味の2系統があり、「推量」系の意味は未定着な人が多いので、それをあわせて問うことができます。
そんなの、テストに出るに決まっています。
まず、基本を確認しましょう。
「許可・義務」系の意味とは?
それは、中学で最初に学習する意味なので、覚えている人もわりと多いのです。
must は、「~しなければならない」
should は、「~するべきだ」
may は、「~してもよい」
can は、「~できる」
では、「推量」系の意味とは?
同じ基本助動詞でも、もう1つの意味がそれぞれあるのです。
すなわち、
must は、「~に違いない」
should は、「~のはずだ」
may は、「~かもしれない」
can は、「~でありうる」
中学の教科書でも一度は出てきているのですが、こちらは覚えていない子が多いのです。
文法事項としてまとめて学習したわけではなく、教科書本文中にこの使い方がさらっと出てきただけなので、記憶が薄いのでしょう。
これらは、日本語でどう訳すのかも含めて正確に覚えておいたほうが、問題を解く際に楽です。
大体のニュアンスで把握しているだけでは、しくじります。
英語を日本語に訳す問題は近年めっきり減りましたが、日本語を英語に直す問題は今も定期テストなどにはよく出題されます。
日本語を見た瞬間、その訳語としての英語を思い浮かべることができないと、正答できません。
今どきの高校生は、「~に違いない」や「~のはずだ」の意味がよくわからない、という子もいます。
普段、そんな言葉遣いをしませんから。
本を読みませんので、そんな言葉遣いを見慣れてもいません。
だから、これは、覚えるしかありません。
この文法事項に限っては、日本語と英語とをイコールで結び、どちらの意味も理解し、覚えましょう。
これは、現実の使える英語の話ではありません。
テスト、特に高校の「論理・表現」のテストでしっかり得点するために行うことです。
もう1点。
must 「~に違いない」の反対は、must not ではありません。
このことは、強く意識して覚えないと、覚えられないのです。
must 「~に違いない」の反対は、cannot 「~のはずがない」です。
これに、should 「~のはずだ」も混ざってくるので、ここで大混乱してしまう子もいます。
間違えやすいところは、ここです。
強く強く意識して、ここを覚えましょう。
さて、そのように基本を確認したところで、いよいよ、「助動詞+have+過去分詞」の用法に入ります。
これは、過去の出来事について、推量的な判断を現在行っている場合に用いるものです。
まずは、普通の文から。
He may read the book.
彼は、その本を読むかもしれない。
これは、現在形。
助動詞の後ろは動詞原形しかきません。
この文は、現在の動作に対して、現在の判断をしていることになります。
でも、過去のことをついて判断したいときもあります。
過去の出来事について、現在の判断をする。
「彼は、その本を読んだかもしれない」
という文を作りたいとき、どうするか?
「かもしれない」という判断をしているのは現在ですから、may は、そのままです。
may を過去形 might にしたところで、過去の意味にはなりません。
意味が和らいで、柔らかい表現になるだけです。
この文は、助動詞を過去形にして解決することではありません。
判断しているのは現在です。
過去の出来事について、現在の判断を下しているのです。
でも、助動詞の後ろを過去形にすることはできない。
それは、英語の根本ルールです。
こんなときに使われるのが、have +過去分詞です。
He may have read the book.
彼は、その本を読んだかもしれない。
これで、過去の出来事を現在判断する文を作ることができました。
これらの用法を、
must have+過去分詞 ~したに違いない。
should have+過去分詞 ~したはずだ。
should have+過去分詞 ~すべきだったのに。
cannot have+過去分詞 ~したはずがない。
may have +過去分詞 ~したのかもしれない。
need not have+過去分詞 ~する必要はなかったのに。
と丸暗記するのがわかりやすいというのなら止めません。
ただ、個々の助動詞の推量系の意味をしっかりと覚え、かつ、have+過去分詞は、過去の出来事について現在の判断をしているのだという把握をしたほうが整理しやすいと思います。
原形を使わなければならない場面で、しかし、過去の意味合いをもたせたいときに、「have+過去分詞」の形を用いるのは、英語の大原則の1つです。
このことを知っていて使いまわせると、今まで覚えにくい、難しいと感じていたところが、一気に簡単になります。
過去の意味合いをもたせたいときに、「have+過去分詞」の形を用いる。
厳密にいえば、時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
繰り返しますが、これは重要ポイントです。
しかし、授業時に解説し板書しても、そのことの重要性に気づかないしノートに取らない子は多いです。
一番大切なところを聞き逃し、ノートにも書かない。
大切なのは、上に書いたような、
must have+過去分詞 ~したに違いない。
should have+過去分詞 ~したはずだ。
should have+過去分詞 ~すべきだったのに。
cannot have+過去分詞 ~したはずがない。
may have +過去分詞 ~したのかもしれない。
need not have+過去分詞 ~する必要はなかったのに。
の一覧だと思い、そして、それはテキストに載っているからまあいいやと、それも書かない。
結果、ノートは真っ白。
勉強が本当に下手なんだなあと思うのです。
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
これは、本当にしばしば使われる英語の大原則なのです。
例えば、「完了形の不定詞」と呼ばれる文法事項。
They seem to build this house. であれば、
「彼らがこの家を建てるようだ」
と、現在の出来事を「~のようだ」と現在判断している文です。
これを、
「彼らがこの家を建てたようだ」
と、過去の出来事を現在判断している文にしたい。
しかし、to の後ろは、動詞の原形しかこないのが不定詞のルール。
このときに、
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
という大原則が生きてきます。
すなわち、
They seem to have built this house.
これで、
「彼らがこの家を建てたようだ」
と過去の出来事を現在判断している文になります。
それが、「完了形の不定詞」という形です。
完了形の不定詞は単純な過去ではなく、「その文の動詞の時制よりも1つ古い時制」を表すものです。
しかし、まずはざっくりと過去になると理解していれば、「1つ古い時制」という無機質な知識も頭に入りやすくなります。
次に、完了形の動名詞。
He is proud of being a mayor.
「彼は、市長であることを誇りに思っている」
現在市長であることを、現在誇りに思っているという文です。
これを、
「彼は、市長だったことを誇りに思っている」
という文にしたいとき。
誇りに思っているのは現在ですが、市長だったのは、過去のことです。
どうしましょう?
動名詞の過去形?
wasing ?
いいえ、そんな形はありません。
He is proud of having been a mayor.
「彼は、市長だったことを誇りに思っている」
1つ古い時制のことを動名詞で表したいときは、「have+過去分詞」のhave の部分をing 形にすればいいのです。
それが、「having+過去分詞」の形です。
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる という大原則が生きてきます。
次に、分詞構文。
まずは、分詞構文を用いる前の、接続詞を用いた文から。
Because she read the novel, she knows the ending of it.
「彼女はその小説を読んだので、その結末を知っている」
その小説を読んだのは、過去のこと。
その結末を知っているのは、現在のこと。
これを分詞構文にしたときに、
Reading the novel, she knows the ending of it.
とすると、時制のズレを表すことができません。
分詞構文にすると、主節の動詞の時制と自動的にそろってしまうからです。
過去のことであることを表したい。
ここで、時制を1つ古くしたいときは「have+過去分詞」の形を用いる という大原則が生きてきます。
Having read the novel, she knows the ending of it.
「彼女はその小説を読んだので、その結末を知っている」
この場合、もとの文が現在完了形だったという把握もできますが、大原則を利用しているのだと頭の隅で理解しておくことで、応用範囲が広がります。
最後に、仮定法。
まずは、仮定法過去。
If I had enough time and money, I would travel around the world.
「十分な時間とお金があれば、私は世界中を旅するだろう」
仮定法のことがわからない場合は、別に仮定法のページをご覧いただければと思いますが、これは仮定法過去。
現在の事実に反する仮定を述べている文です。
現在の事実に反するので、その心理的距離間を時制のズレで表しているのだろうと言われています。
if 節は、過去形。
主節は、主語+助動詞過去形+動詞原形。
この形で、現在の事実に反する仮定を表します。
しかし、人は、過去の事実に反する仮定を言いたいときもあります。
あのとき、ああだったらなあ、と。
言っても仕方のない「たら・れば」ですが、言いたいときはあります。
それが、仮定法過去完了。
過去の事実に反する仮定を表すものです。
過去よりも1つ時制を古くするのなら、if 節は、過去完了形。
それは、ピンときます。
でも、主節は?
助動詞に過去完了の形などあるはずがありません。
そして、助動詞の後ろは、動詞原形でなければなりません。
ここで登場するのが、「have+過去分詞」です。
If I had had enough time and money, I would have traveled around the world.
「私に十分な時間とお金があったら、私は世界中を旅しただろう」
時制を1つ古くしたいときは、「have+過去分詞」。
この原則が、他の文法事項、特に覚えにくいところで多用されています。
大原則を理解すれば楽になります。
英語の秀才は、そこを理解しています。
しかし、そのことに気づかず、むしろ、何だか似たようなことを前にも習ったようで、混ざって余計に混乱する、としか把握できない・・・。
勉強が下手というのは、そういうことです。
そして、前に学習したことを定期テストが終われば簡単に記憶から消去しているから、そういうことになるのでもあるのだと思うのです。
忘れてはいけない。
一度頭に入れた知識は、忘れないように反復しましょう。
そういう知識は、「3日前の夕飯は何を食べた」といった、どうでもいい記憶とは区別して、しっかり覚えておきましょう。
全部短期記憶にして、全部捨てていくことを、自分の中で肯定するのはやめましょう。
学力が低い人は、記憶がないのです。
本当に、不可解なほど、何も覚えていないのです。
まず、記憶を確保しましょう。
基本的な助動詞は、「許可・義務」系の意味と「推量」系の意味の2系統があり、「推量」系の意味は未定着な人が多いので、それをあわせて問うことができます。
そんなの、テストに出るに決まっています。
まず、基本を確認しましょう。
「許可・義務」系の意味とは?
それは、中学で最初に学習する意味なので、覚えている人もわりと多いのです。
must は、「~しなければならない」
should は、「~するべきだ」
may は、「~してもよい」
can は、「~できる」
では、「推量」系の意味とは?
同じ基本助動詞でも、もう1つの意味がそれぞれあるのです。
すなわち、
must は、「~に違いない」
should は、「~のはずだ」
may は、「~かもしれない」
can は、「~でありうる」
中学の教科書でも一度は出てきているのですが、こちらは覚えていない子が多いのです。
文法事項としてまとめて学習したわけではなく、教科書本文中にこの使い方がさらっと出てきただけなので、記憶が薄いのでしょう。
これらは、日本語でどう訳すのかも含めて正確に覚えておいたほうが、問題を解く際に楽です。
大体のニュアンスで把握しているだけでは、しくじります。
英語を日本語に訳す問題は近年めっきり減りましたが、日本語を英語に直す問題は今も定期テストなどにはよく出題されます。
日本語を見た瞬間、その訳語としての英語を思い浮かべることができないと、正答できません。
今どきの高校生は、「~に違いない」や「~のはずだ」の意味がよくわからない、という子もいます。
普段、そんな言葉遣いをしませんから。
本を読みませんので、そんな言葉遣いを見慣れてもいません。
だから、これは、覚えるしかありません。
この文法事項に限っては、日本語と英語とをイコールで結び、どちらの意味も理解し、覚えましょう。
これは、現実の使える英語の話ではありません。
テスト、特に高校の「論理・表現」のテストでしっかり得点するために行うことです。
もう1点。
must 「~に違いない」の反対は、must not ではありません。
このことは、強く意識して覚えないと、覚えられないのです。
must 「~に違いない」の反対は、cannot 「~のはずがない」です。
これに、should 「~のはずだ」も混ざってくるので、ここで大混乱してしまう子もいます。
間違えやすいところは、ここです。
強く強く意識して、ここを覚えましょう。
さて、そのように基本を確認したところで、いよいよ、「助動詞+have+過去分詞」の用法に入ります。
これは、過去の出来事について、推量的な判断を現在行っている場合に用いるものです。
まずは、普通の文から。
He may read the book.
彼は、その本を読むかもしれない。
これは、現在形。
助動詞の後ろは動詞原形しかきません。
この文は、現在の動作に対して、現在の判断をしていることになります。
でも、過去のことをついて判断したいときもあります。
過去の出来事について、現在の判断をする。
「彼は、その本を読んだかもしれない」
という文を作りたいとき、どうするか?
「かもしれない」という判断をしているのは現在ですから、may は、そのままです。
may を過去形 might にしたところで、過去の意味にはなりません。
意味が和らいで、柔らかい表現になるだけです。
この文は、助動詞を過去形にして解決することではありません。
判断しているのは現在です。
過去の出来事について、現在の判断を下しているのです。
でも、助動詞の後ろを過去形にすることはできない。
それは、英語の根本ルールです。
こんなときに使われるのが、have +過去分詞です。
He may have read the book.
彼は、その本を読んだかもしれない。
これで、過去の出来事を現在判断する文を作ることができました。
これらの用法を、
must have+過去分詞 ~したに違いない。
should have+過去分詞 ~したはずだ。
should have+過去分詞 ~すべきだったのに。
cannot have+過去分詞 ~したはずがない。
may have +過去分詞 ~したのかもしれない。
need not have+過去分詞 ~する必要はなかったのに。
と丸暗記するのがわかりやすいというのなら止めません。
ただ、個々の助動詞の推量系の意味をしっかりと覚え、かつ、have+過去分詞は、過去の出来事について現在の判断をしているのだという把握をしたほうが整理しやすいと思います。
原形を使わなければならない場面で、しかし、過去の意味合いをもたせたいときに、「have+過去分詞」の形を用いるのは、英語の大原則の1つです。
このことを知っていて使いまわせると、今まで覚えにくい、難しいと感じていたところが、一気に簡単になります。
過去の意味合いをもたせたいときに、「have+過去分詞」の形を用いる。
厳密にいえば、時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
繰り返しますが、これは重要ポイントです。
しかし、授業時に解説し板書しても、そのことの重要性に気づかないしノートに取らない子は多いです。
一番大切なところを聞き逃し、ノートにも書かない。
大切なのは、上に書いたような、
must have+過去分詞 ~したに違いない。
should have+過去分詞 ~したはずだ。
should have+過去分詞 ~すべきだったのに。
cannot have+過去分詞 ~したはずがない。
may have +過去分詞 ~したのかもしれない。
need not have+過去分詞 ~する必要はなかったのに。
の一覧だと思い、そして、それはテキストに載っているからまあいいやと、それも書かない。
結果、ノートは真っ白。
勉強が本当に下手なんだなあと思うのです。
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
これは、本当にしばしば使われる英語の大原則なのです。
例えば、「完了形の不定詞」と呼ばれる文法事項。
They seem to build this house. であれば、
「彼らがこの家を建てるようだ」
と、現在の出来事を「~のようだ」と現在判断している文です。
これを、
「彼らがこの家を建てたようだ」
と、過去の出来事を現在判断している文にしたい。
しかし、to の後ろは、動詞の原形しかこないのが不定詞のルール。
このときに、
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる。
という大原則が生きてきます。
すなわち、
They seem to have built this house.
これで、
「彼らがこの家を建てたようだ」
と過去の出来事を現在判断している文になります。
それが、「完了形の不定詞」という形です。
完了形の不定詞は単純な過去ではなく、「その文の動詞の時制よりも1つ古い時制」を表すものです。
しかし、まずはざっくりと過去になると理解していれば、「1つ古い時制」という無機質な知識も頭に入りやすくなります。
次に、完了形の動名詞。
He is proud of being a mayor.
「彼は、市長であることを誇りに思っている」
現在市長であることを、現在誇りに思っているという文です。
これを、
「彼は、市長だったことを誇りに思っている」
という文にしたいとき。
誇りに思っているのは現在ですが、市長だったのは、過去のことです。
どうしましょう?
動名詞の過去形?
wasing ?
いいえ、そんな形はありません。
He is proud of having been a mayor.
「彼は、市長だったことを誇りに思っている」
1つ古い時制のことを動名詞で表したいときは、「have+過去分詞」のhave の部分をing 形にすればいいのです。
それが、「having+過去分詞」の形です。
時制を1つ古くしたいときは、「have+過去分詞」の形を用いる という大原則が生きてきます。
次に、分詞構文。
まずは、分詞構文を用いる前の、接続詞を用いた文から。
Because she read the novel, she knows the ending of it.
「彼女はその小説を読んだので、その結末を知っている」
その小説を読んだのは、過去のこと。
その結末を知っているのは、現在のこと。
これを分詞構文にしたときに、
Reading the novel, she knows the ending of it.
とすると、時制のズレを表すことができません。
分詞構文にすると、主節の動詞の時制と自動的にそろってしまうからです。
過去のことであることを表したい。
ここで、時制を1つ古くしたいときは「have+過去分詞」の形を用いる という大原則が生きてきます。
Having read the novel, she knows the ending of it.
「彼女はその小説を読んだので、その結末を知っている」
この場合、もとの文が現在完了形だったという把握もできますが、大原則を利用しているのだと頭の隅で理解しておくことで、応用範囲が広がります。
最後に、仮定法。
まずは、仮定法過去。
If I had enough time and money, I would travel around the world.
「十分な時間とお金があれば、私は世界中を旅するだろう」
仮定法のことがわからない場合は、別に仮定法のページをご覧いただければと思いますが、これは仮定法過去。
現在の事実に反する仮定を述べている文です。
現在の事実に反するので、その心理的距離間を時制のズレで表しているのだろうと言われています。
if 節は、過去形。
主節は、主語+助動詞過去形+動詞原形。
この形で、現在の事実に反する仮定を表します。
しかし、人は、過去の事実に反する仮定を言いたいときもあります。
あのとき、ああだったらなあ、と。
言っても仕方のない「たら・れば」ですが、言いたいときはあります。
それが、仮定法過去完了。
過去の事実に反する仮定を表すものです。
過去よりも1つ時制を古くするのなら、if 節は、過去完了形。
それは、ピンときます。
でも、主節は?
助動詞に過去完了の形などあるはずがありません。
そして、助動詞の後ろは、動詞原形でなければなりません。
ここで登場するのが、「have+過去分詞」です。
If I had had enough time and money, I would have traveled around the world.
「私に十分な時間とお金があったら、私は世界中を旅しただろう」
時制を1つ古くしたいときは、「have+過去分詞」。
この原則が、他の文法事項、特に覚えにくいところで多用されています。
大原則を理解すれば楽になります。
英語の秀才は、そこを理解しています。
しかし、そのことに気づかず、むしろ、何だか似たようなことを前にも習ったようで、混ざって余計に混乱する、としか把握できない・・・。
勉強が下手というのは、そういうことです。
そして、前に学習したことを定期テストが終われば簡単に記憶から消去しているから、そういうことになるのでもあるのだと思うのです。
忘れてはいけない。
一度頭に入れた知識は、忘れないように反復しましょう。
そういう知識は、「3日前の夕飯は何を食べた」といった、どうでもいい記憶とは区別して、しっかり覚えておきましょう。
全部短期記憶にして、全部捨てていくことを、自分の中で肯定するのはやめましょう。
学力が低い人は、記憶がないのです。
本当に、不可解なほど、何も覚えていないのです。
まず、記憶を確保しましょう。
2022年09月17日
三か月ぶりに都立小金井公園まで歩きながら、セミとカラスと英語のことを考えました。

2022年9月16日(金)、久しぶりに散歩に出かけました。
今年は、6月に早くも猛暑日になってしまいました。
そこでもう気持ちが折れて、部屋でときどきビリーズブートキャンプをやっていましたが、まあ全体に運動不足です。
コロナが少しは落ち着いてきて、今年も秋には山に行けるかも。
その準備も兼ねて、足慣らしの散歩に出かけました。
いつものように、三鷹駅北口から、玉川上水緑道を西へ。
ミンミンゼミがまだ鳴いているのに驚きました。
セミの寿命は地上で7日間ではなく約1か月。
とはいえ、うちの近所のセミは、8月で姿を消しました。
まだ鳴いているんですね、セミ。
住居の通路脇の木は、2年ほど前に枝をすべて切り落とされたのですが、木の生命力というのは凄いもので、今年の夏はそれまで以上に枝を広げ、通路にかかっていました。
その木に棲むセミが、なかなかの暴れ者。
8月中は通路でセミから逃走する日々でした。
おとなしくしてくれていれば何もしないのに、通路を歩く人の気配に勝手に「ギチチー」と鳴いて威嚇するセミ。
それだけならいいのですが、驚いて飛ぶセミもいます。
セミは目があまりよくないのだそうで、通路に飛び出してしまうと、壁や天井にガチンガチンぶつかって、スマートボールのようです。
木に戻れないのですね。
下手をすると、こちらに襲いかかってきます。
まかり間違って、ドアから部屋に入ってきたら、最悪です。
憂鬱なひと月でした。
もう、すっかりセミが嫌いになりました。
とはいえ、その木にはスズメも来るので、ある程度はスズメがセミを捕食してくれて、それでいなくなるのが早かったのかもしれません。
今はもう、秋の虫の声しか聞こえない平和な通路です。
夏から秋へのはざまの玉川上水緑道。
境の浄水場を越えて、桜橋を右折。
次の交差点で井の頭通りを左折。
細長い公園を歩いていき、大きな交差点を渡ると、多摩湖自転車歩行者道。
狭山境緑道です。
片耳イヤホンで聴くのは、ラジオの英語講座の録音。
夏期講習の忙しさにかまけてたまってしまい、まだ8月末の放送の録音を聞いています。
ためてはいますが、今までもそうだったように、いずれ追いつきます。
土日は放送がないので、その分だけ、週に2日ずつ追いつけると思います。
英語と言えば、都立高校を受験する中3生徒が対象の英語スピーキングテストの問題点がようやく世間に知られるようになってきました。
保護者の方たちの反対運動も活発化し、都議会も動き始めています。
それでも、まだ動きが遅く、心配です。
このテストが行われるのは、今年度が初めてです。
何とか中止にできないものか。
英語のスピーキングテスト。
受験する高校の英語の先生が採点するというのなら、わかります。
民間企業が問題を作り、その民間企業が採点も請け負い、海外の誰か(バイト?)に採点させる。
そんなことで公平性が担保できるとは思えません。
それが、都立高校入試に加点される。
こんなバカな話が、何でここまで実現化しているのでしょう。
ありえないでしょう・・・。
大学入試の民間英語テスト導入をぎりぎりで阻止できたように、今回もどうにか阻止できるといいのですが。
教育を金儲けに利用するのが悪とは言いませんし、私もその一端に属するものですが、節度というものがあります。
受験の内側に汚い手を突っ込んではいけない。
教育産業は、あくまでも外部から生徒を支え、志望校合格に導き、その対価をもらう商売だと思うんですよ。
塾経営も。
教材を作る企業も。
模試を運営する企業も。
そんなことをつらつら考えながら、小学校前の土手に上がり、銀色の道しるべを見下ろして、左折。
水路の脇の道を行き、鈴木街道の交差点を渡ると、都立小金井公園です。
いきなり、ヒマワリの黄色い帯が目をひきました。
まだ、ヒマワリが咲いています。
コスモスも咲き始めていました。
これからの最盛期に備えてか、コスモス畑の周囲では草刈りが行われていました。
いつものように、できるだけ土の道を、公園北西部まで歩き、キキョウなど撮影して、もと来た道を戻りました。
あれ?
カラスがいない。
気がつくと、1羽もいないのです。
前回、私はカラスに威嚇されました。
私だけだったとは思えません。
ここは子ども向けの施設のある公園。
子どもがカラスに襲われたりすると怖いから、駆除されたのでしょうか。
うーん。
ヒナを育てている時期以外は、そんなに人間に危害を加えてこないと思うけれど、カラスは大きいから、やっぱりちょっと怖いですよね。
私はセミのほうが怖いですが。
セミのあの闇雲感が怖い。
カラスは賢いから、意味のない行動はとらない。
さて、正門から、帰ろう。
信号を渡って、玉川上水緑道を東へと戻ります。
上水の右岸を行くと、途中からは草むらに変わり、かなり歩きにくくなっていました。
ここを歩く人はしばらくいなかったのかというほどに。
ここも、やがて草刈りされるのでしょう。
気温は30度までには至らず、それなりに風もあるけれど、3か月ぶりの散歩はやはり少しこたえます。
疲れてきました。
三鷹への道を遠く感じました。
もう少し身体を慣らさないと。
ときどき見えるヒガンバナ。
濃い赤が、玉川上水の深い草むらの奥でも目をひきます。
少しずつ秋が来ています。
1週1週涼しくなるから、その分、散歩も楽になるでしょう。
都内のコロナ感染者は、1万人を切る日も多くなってきましたが、去年のように千人以下にまでは下がらないのでしょうか。
どこらへんで見極めて山に行くことにしようかと考慮中です。
今年は、6月に早くも猛暑日になってしまいました。
そこでもう気持ちが折れて、部屋でときどきビリーズブートキャンプをやっていましたが、まあ全体に運動不足です。
コロナが少しは落ち着いてきて、今年も秋には山に行けるかも。
その準備も兼ねて、足慣らしの散歩に出かけました。
いつものように、三鷹駅北口から、玉川上水緑道を西へ。
ミンミンゼミがまだ鳴いているのに驚きました。
セミの寿命は地上で7日間ではなく約1か月。
とはいえ、うちの近所のセミは、8月で姿を消しました。
まだ鳴いているんですね、セミ。
住居の通路脇の木は、2年ほど前に枝をすべて切り落とされたのですが、木の生命力というのは凄いもので、今年の夏はそれまで以上に枝を広げ、通路にかかっていました。
その木に棲むセミが、なかなかの暴れ者。
8月中は通路でセミから逃走する日々でした。
おとなしくしてくれていれば何もしないのに、通路を歩く人の気配に勝手に「ギチチー」と鳴いて威嚇するセミ。
それだけならいいのですが、驚いて飛ぶセミもいます。
セミは目があまりよくないのだそうで、通路に飛び出してしまうと、壁や天井にガチンガチンぶつかって、スマートボールのようです。
木に戻れないのですね。
下手をすると、こちらに襲いかかってきます。
まかり間違って、ドアから部屋に入ってきたら、最悪です。
憂鬱なひと月でした。
もう、すっかりセミが嫌いになりました。
とはいえ、その木にはスズメも来るので、ある程度はスズメがセミを捕食してくれて、それでいなくなるのが早かったのかもしれません。
今はもう、秋の虫の声しか聞こえない平和な通路です。
夏から秋へのはざまの玉川上水緑道。
境の浄水場を越えて、桜橋を右折。
次の交差点で井の頭通りを左折。
細長い公園を歩いていき、大きな交差点を渡ると、多摩湖自転車歩行者道。
狭山境緑道です。
片耳イヤホンで聴くのは、ラジオの英語講座の録音。
夏期講習の忙しさにかまけてたまってしまい、まだ8月末の放送の録音を聞いています。
ためてはいますが、今までもそうだったように、いずれ追いつきます。
土日は放送がないので、その分だけ、週に2日ずつ追いつけると思います。
英語と言えば、都立高校を受験する中3生徒が対象の英語スピーキングテストの問題点がようやく世間に知られるようになってきました。
保護者の方たちの反対運動も活発化し、都議会も動き始めています。
それでも、まだ動きが遅く、心配です。
このテストが行われるのは、今年度が初めてです。
何とか中止にできないものか。
英語のスピーキングテスト。
受験する高校の英語の先生が採点するというのなら、わかります。
民間企業が問題を作り、その民間企業が採点も請け負い、海外の誰か(バイト?)に採点させる。
そんなことで公平性が担保できるとは思えません。
それが、都立高校入試に加点される。
こんなバカな話が、何でここまで実現化しているのでしょう。
ありえないでしょう・・・。
大学入試の民間英語テスト導入をぎりぎりで阻止できたように、今回もどうにか阻止できるといいのですが。
教育を金儲けに利用するのが悪とは言いませんし、私もその一端に属するものですが、節度というものがあります。
受験の内側に汚い手を突っ込んではいけない。
教育産業は、あくまでも外部から生徒を支え、志望校合格に導き、その対価をもらう商売だと思うんですよ。
塾経営も。
教材を作る企業も。
模試を運営する企業も。
そんなことをつらつら考えながら、小学校前の土手に上がり、銀色の道しるべを見下ろして、左折。
水路の脇の道を行き、鈴木街道の交差点を渡ると、都立小金井公園です。
いきなり、ヒマワリの黄色い帯が目をひきました。
まだ、ヒマワリが咲いています。
コスモスも咲き始めていました。
これからの最盛期に備えてか、コスモス畑の周囲では草刈りが行われていました。
いつものように、できるだけ土の道を、公園北西部まで歩き、キキョウなど撮影して、もと来た道を戻りました。
あれ?
カラスがいない。
気がつくと、1羽もいないのです。
前回、私はカラスに威嚇されました。
私だけだったとは思えません。
ここは子ども向けの施設のある公園。
子どもがカラスに襲われたりすると怖いから、駆除されたのでしょうか。
うーん。
ヒナを育てている時期以外は、そんなに人間に危害を加えてこないと思うけれど、カラスは大きいから、やっぱりちょっと怖いですよね。
私はセミのほうが怖いですが。
セミのあの闇雲感が怖い。
カラスは賢いから、意味のない行動はとらない。
さて、正門から、帰ろう。
信号を渡って、玉川上水緑道を東へと戻ります。
上水の右岸を行くと、途中からは草むらに変わり、かなり歩きにくくなっていました。
ここを歩く人はしばらくいなかったのかというほどに。
ここも、やがて草刈りされるのでしょう。
気温は30度までには至らず、それなりに風もあるけれど、3か月ぶりの散歩はやはり少しこたえます。
疲れてきました。
三鷹への道を遠く感じました。
もう少し身体を慣らさないと。
ときどき見えるヒガンバナ。
濃い赤が、玉川上水の深い草むらの奥でも目をひきます。
少しずつ秋が来ています。
1週1週涼しくなるから、その分、散歩も楽になるでしょう。
都内のコロナ感染者は、1万人を切る日も多くなってきましたが、去年のように千人以下にまでは下がらないのでしょうか。
どこらへんで見極めて山に行くことにしようかと考慮中です。
2022年09月12日
厚紙を折って、容器を作る問題。
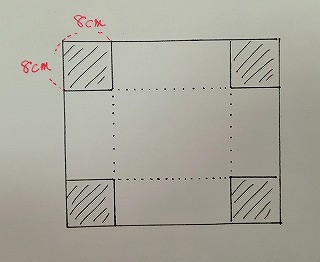
問題 横が縦より5㎝長い長方形の厚紙がある。この紙の四すみから図のように1辺が8㎝の正方形を切り取り、折り曲げて直方体の容器を作ったところ、容積が2400㎤になった。もとの厚紙の縦と横の長さを求めなさい。ただし、紙の厚さは考えないものとする。
問題に図が添えられてあると、図ばかり見て、問題を読まない子がいます。
図だけを見て、考え込んでいます。
「問題の意味はわかる?」
と問いかけると、首をひねっています。
図だけでは情報が少なく、重要な情報は問題文中にあるのに、そのことに気づかないのです。
たとえば、この問題では、「縦が横より5㎝長い」という重要な情報があるのに、そのことに気づかない。
問題文を読み聞かせてあげると、「ああ、そうか」と言ったりします。
自分で読めばいいだけなのに・・・。
問題文を読まないで解くことが癖になっている子は、こうした数学の文章題だけでなく、国語も英語も本文を読まないで解いてしまうことがあります。
問題文の傍線部や( )の前後だけをちょろちょろっと斜め読みして、それで答えてしまうのです。
しかし、今どきのテストは、四択問題でも、そのような子をひっかけて誤答させる選択肢を作ってあります。
そんな読み方をしていると、正答できません。
問題文を全文読み、書いてあることを書いてある通りに読み取れる子が正答できるように問題を作ってあるのです。
当然です。
文章を読みたくない子は、大学に入っても意味がありません。
学問は、文章を読み、書くことが基本です。
多くの論文を読み、討論し調査し実験し、自分の論文を書く。
研究結果を客観的に他人に伝える手段は、文系理系を問わず、文章です。
文章を読むのがそんなに嫌いなら、大学に行く必要はないのです。
大学を、テストでよい点を取って卒業するだけの場所だと思っているのでしょうか。
その後は、どうするのでしょう。
文章を読む力がなく、文章を読むのが嫌いなのに、何の仕事をするのでしょうか。
書類を読めなくてもできる仕事はあると思いますが、それは、大卒の資格が必要な仕事でしょうか。
本人はわりと気軽に考えているのだと思いますが、問題文を読むか読まないかは、人生を左右します。
問題文を読まない子は、おそらく、小学校の4年生くらいには、そういう読み方の癖がついていたと思います。
そのまま、例えば中3まで、5~6年間、問題文を読まないで勉強をしてきたのでしょうか。
では、読解力は、小4のままでしょう。
小学校4年生の読解力で中学の問題文を読もうとしても、力がありませんから上手く読めないでしょう。
ますます問題文を読まなくなります。
「問題文を読まない子」だったのが、もはや「問題文を読めない子」になっています。
読んでも、難しくて意味を取れないのです。
5~6年間のブランクは大きいです。
その子よりももっと文字を読むことが能力的につらく、そこに課題のあった子の中には、それでも、その5年間、地道に問題文を読み続け、その能力を着実に伸ばしてきた子もいるでしょうに。
暗澹たる思いにとらわれます。
何でそんなふうに何年も時間を空費してしまったのか。
とはいえ、大学入試まではまだ時間があります。
今から問題文を読むようにすれば、努力次第でどうにでもなります。
文章を読まないことで自分が招いてしまった学習の遅れは、自分の努力で補えばよいのです。
問題文を読むようになり、そこから飛躍した子もいます。
我慢できるかどうか、そこが分かれ道です。
図だけでなく、問題文を読んでください。
もう一度問題を。
問題 横が縦より5㎝長い長方形の厚紙がある。この紙の四すみから1辺が8㎝の正方形を切り取り、折り曲げて直方体の容器を作ったところ、容積が2400㎤になった。もとの厚紙の縦と横の長さを求めなさい。ただし、紙の厚さは考えないものとする。
これは、中3「2次方程式の利用」の問題ですが、小学生でも解くことは可能です。
受験算数にも、このような問題はあります。
まずは、受験算数で解いてみましょう。
出来上がった直方体の容器の高さは、8㎝です。
では、容積から、底面積を求めましょう。
2400÷8=300
底面積は、300㎠です。
もとの厚紙の横が縦より5㎝長く、切り取った四すみは8㎝ずつと同じ長さです。
したがって、出来上がった直方体の容器の底面も、横が縦より5㎝長いのです。
ですから、
〇×△=300
の式を満たして、〇と△が5つ違いである2つの数を見つければよいのです。
ここで、何か式を立てることしか発想できない頭の固い子は、ここまで、となります。
小学生の場合、上の〇×△=300 を満たす〇と△は、式を立てて求めるのではなく、勘と努力で求めることになります。
大体このくらいの数だろうとあたりをつけて、実際にかけ算をして求めていきます。
ですから、これは、数に対する感覚が発達しているかどうかを問う問題です。
積が300で、差が5の数?
ピンとくる子は、一度で発見します。
15×20=300 です。
よって、底面の縦は15㎝、横は20㎝。
四すみを8㎝ずつ切り取ってそれなのですから、その四すみの分、8×2=16㎝をたして、
もとの厚紙の縦は31㎝、横は36㎝。
これが答です。
さて、同じ問題も、中3ならば、もっとスマートに解くことができます。
求めるものをxとして、方程式を立てましょう。
もとの厚紙の縦の長さをx㎝とする。
すると、横は(x+5)㎝と表されます。
方程式は、容器の容積を表すものを作りましょう。
直方体の容器ですから、縦×横×高さ=容積です。
四隅から8㎝ずつ切り取ってありますから、
容器の縦は、(x-16)㎝、横は(x+5-16)㎝です。
よって、方程式は、
8(x-16)(x+5-16)=2400
こういうときは、まず、両辺を8で割りましょう。
(x-16)(x-11)=300
x^2-27x+176-300=0
x^2-27x-124=0
(x+4)(x-31)=0
x=-4、31
四隅から8㎝ずつ切り取ることができたのですから、
x>16より、
x=31
よって、厚紙の縦31㎝、横36㎝です。
ところで、この問題を解説していて、不思議な質問を受けたことがありました。
厚紙の縦をx㎝としたのだから、容器の容積をxを使って表すことはできないというのです。
厚紙の縦をx㎝としたのだから、厚紙の面積しか表すことはできない。
容器の底面の縦はx㎝ではないのだから、容器の容積をxを使って表すことはできない。
そう言うのでした。
方程式を立てられない子の思考の一端が垣間見えて、興味深い質問でした。
問題に図が添えられてあると、図ばかり見て、問題を読まない子がいます。
図だけを見て、考え込んでいます。
「問題の意味はわかる?」
と問いかけると、首をひねっています。
図だけでは情報が少なく、重要な情報は問題文中にあるのに、そのことに気づかないのです。
たとえば、この問題では、「縦が横より5㎝長い」という重要な情報があるのに、そのことに気づかない。
問題文を読み聞かせてあげると、「ああ、そうか」と言ったりします。
自分で読めばいいだけなのに・・・。
問題文を読まないで解くことが癖になっている子は、こうした数学の文章題だけでなく、国語も英語も本文を読まないで解いてしまうことがあります。
問題文の傍線部や( )の前後だけをちょろちょろっと斜め読みして、それで答えてしまうのです。
しかし、今どきのテストは、四択問題でも、そのような子をひっかけて誤答させる選択肢を作ってあります。
そんな読み方をしていると、正答できません。
問題文を全文読み、書いてあることを書いてある通りに読み取れる子が正答できるように問題を作ってあるのです。
当然です。
文章を読みたくない子は、大学に入っても意味がありません。
学問は、文章を読み、書くことが基本です。
多くの論文を読み、討論し調査し実験し、自分の論文を書く。
研究結果を客観的に他人に伝える手段は、文系理系を問わず、文章です。
文章を読むのがそんなに嫌いなら、大学に行く必要はないのです。
大学を、テストでよい点を取って卒業するだけの場所だと思っているのでしょうか。
その後は、どうするのでしょう。
文章を読む力がなく、文章を読むのが嫌いなのに、何の仕事をするのでしょうか。
書類を読めなくてもできる仕事はあると思いますが、それは、大卒の資格が必要な仕事でしょうか。
本人はわりと気軽に考えているのだと思いますが、問題文を読むか読まないかは、人生を左右します。
問題文を読まない子は、おそらく、小学校の4年生くらいには、そういう読み方の癖がついていたと思います。
そのまま、例えば中3まで、5~6年間、問題文を読まないで勉強をしてきたのでしょうか。
では、読解力は、小4のままでしょう。
小学校4年生の読解力で中学の問題文を読もうとしても、力がありませんから上手く読めないでしょう。
ますます問題文を読まなくなります。
「問題文を読まない子」だったのが、もはや「問題文を読めない子」になっています。
読んでも、難しくて意味を取れないのです。
5~6年間のブランクは大きいです。
その子よりももっと文字を読むことが能力的につらく、そこに課題のあった子の中には、それでも、その5年間、地道に問題文を読み続け、その能力を着実に伸ばしてきた子もいるでしょうに。
暗澹たる思いにとらわれます。
何でそんなふうに何年も時間を空費してしまったのか。
とはいえ、大学入試まではまだ時間があります。
今から問題文を読むようにすれば、努力次第でどうにでもなります。
文章を読まないことで自分が招いてしまった学習の遅れは、自分の努力で補えばよいのです。
問題文を読むようになり、そこから飛躍した子もいます。
我慢できるかどうか、そこが分かれ道です。
図だけでなく、問題文を読んでください。
もう一度問題を。
問題 横が縦より5㎝長い長方形の厚紙がある。この紙の四すみから1辺が8㎝の正方形を切り取り、折り曲げて直方体の容器を作ったところ、容積が2400㎤になった。もとの厚紙の縦と横の長さを求めなさい。ただし、紙の厚さは考えないものとする。
これは、中3「2次方程式の利用」の問題ですが、小学生でも解くことは可能です。
受験算数にも、このような問題はあります。
まずは、受験算数で解いてみましょう。
出来上がった直方体の容器の高さは、8㎝です。
では、容積から、底面積を求めましょう。
2400÷8=300
底面積は、300㎠です。
もとの厚紙の横が縦より5㎝長く、切り取った四すみは8㎝ずつと同じ長さです。
したがって、出来上がった直方体の容器の底面も、横が縦より5㎝長いのです。
ですから、
〇×△=300
の式を満たして、〇と△が5つ違いである2つの数を見つければよいのです。
ここで、何か式を立てることしか発想できない頭の固い子は、ここまで、となります。
小学生の場合、上の〇×△=300 を満たす〇と△は、式を立てて求めるのではなく、勘と努力で求めることになります。
大体このくらいの数だろうとあたりをつけて、実際にかけ算をして求めていきます。
ですから、これは、数に対する感覚が発達しているかどうかを問う問題です。
積が300で、差が5の数?
ピンとくる子は、一度で発見します。
15×20=300 です。
よって、底面の縦は15㎝、横は20㎝。
四すみを8㎝ずつ切り取ってそれなのですから、その四すみの分、8×2=16㎝をたして、
もとの厚紙の縦は31㎝、横は36㎝。
これが答です。
さて、同じ問題も、中3ならば、もっとスマートに解くことができます。
求めるものをxとして、方程式を立てましょう。
もとの厚紙の縦の長さをx㎝とする。
すると、横は(x+5)㎝と表されます。
方程式は、容器の容積を表すものを作りましょう。
直方体の容器ですから、縦×横×高さ=容積です。
四隅から8㎝ずつ切り取ってありますから、
容器の縦は、(x-16)㎝、横は(x+5-16)㎝です。
よって、方程式は、
8(x-16)(x+5-16)=2400
こういうときは、まず、両辺を8で割りましょう。
(x-16)(x-11)=300
x^2-27x+176-300=0
x^2-27x-124=0
(x+4)(x-31)=0
x=-4、31
四隅から8㎝ずつ切り取ることができたのですから、
x>16より、
x=31
よって、厚紙の縦31㎝、横36㎝です。
ところで、この問題を解説していて、不思議な質問を受けたことがありました。
厚紙の縦をx㎝としたのだから、容器の容積をxを使って表すことはできないというのです。
厚紙の縦をx㎝としたのだから、厚紙の面積しか表すことはできない。
容器の底面の縦はx㎝ではないのだから、容器の容積をxを使って表すことはできない。
そう言うのでした。
方程式を立てられない子の思考の一端が垣間見えて、興味深い質問でした。
2022年09月08日
高校英語。同格のthat
まずは問題から。
問題 次の文の that と同じ働きの that を含む文を以下の(1)~(4)から選べ。
He coughed to give her the hint that she should leave the room.
(1) He couldn't make it clear that he had nothing to do with the accident.
(2) It was a dog that he caught in that mountain.
(3) He heard a rumor that wolves lived in that mountain.
(4) He knows the fact that she is trying to conceal.
色々な that があって、ちょっと難しいですね。
そもそも、一番上の問題文の that は、どういう that なのでしょうか。
この文は「その部屋を出るべきだというヒントを彼女に与えるために、彼は咳払いをした」という意味です。
He coughed という部分が、S(主語)とV(動詞)です。
その後ろは、副詞的用法の不定詞。「~するために」という意味です。
その不定詞の中で、また、V・O・Oという構造になっています。
give が不定詞の中でのV。
her が、不定詞の中でのO(目的語)。
the hint が、不定詞の中でのもう1つのO(目的語)です。
「誰々に」「何々を」の語順で、2つの目的語をもっている動詞ということです。
では、その後ろのthat 節は、何なのか?
これは、the hint の中身を説明しています。
どういうヒントであるのかを具体的に説明しているのです。
「彼女はその部屋を出るべきだ」というヒントです。
したがって、この that は、
the hint と she should leave the room を対等に結んでいます。
これを「同格の that」と呼びます。
接続詞 that の用法の1つです。
では、(1)~(4)で、同格の that はどれでしょうか。
1つ1つ見ていきましょう。
(1) He couldn't make it clear that he had nothing to do with the accident.
「彼は、その事故と関係がないことを明らかにすることができなかった」
この文は、同格の that ではないことは、比較的に簡単に見分けることができると思います。
He couldn't make it clear
までで、S・V・O・C です。
it は形式目的語。
目的語が長い内容なので、とりあえず it を立てて、Cを言ってから、ゆっくりと最後に it の中身を語っていく形の文です。
it =that he had nothing to do with the accident
です。
こういうのは「同格の that」とは言いません。
同格の that は、名詞の直後に置いてその名詞の中身を説明するもので、it のような代名詞の中身を説明するものではありません。
これも接続詞の that ではありますが、これは、真の目的語の that 節です。
(2) It was a dog that he caught in that mountain.
これは何でしょう?
「それは、彼が山の中で捕まえた犬だった」
という文でしょうか?
だとすれば、この that は、dog を修飾する関係代名詞の that です。
文脈によっては、そのような意味にとっても良いと思います。
あるいは、これは強調構文かもしれません。
it is ~ that で、強調したい内容を挟む、強調構文です。
そうだとすれば、
「彼がその山の中で捕まえたのは、犬だった」
となります。
いずれにせよ、「同格の that」ではありません。
(3) He heard a rumor that wolves lived in that mountain.
「彼は、オオカミがその山に住んでいるという噂を聞いた」という文です。
a rumor = wolves lived in that mountain
まさに、「同格の that」。
これが正解でしょう。
しかし、(4) を見て、「うん?」となる人は多いと思います。
(4) He knows the fact that she is trying to conceal.
「彼は、彼女が隠そうとしている事実を知っている」
これも「同格の that」なのではないか?
同格の that は、どんな名詞の後でも使用できるものではありません。
同格の that を使える名詞は限られていて、その名詞を覚えている人も多いと思います。
その中で、the fact that ~という用法は典型的なもので、例文でよく使われています。
では、(4) も同格の that なのでしょうか。
これが違うのです。
この that は、関係代名詞です。
ここで問題となるのが、
接続詞の that と、関係代名詞の that は、どう区別するか?
ということでしょう。
見分けは、それほど難しくありません。
関係代名詞の that は、その関係詞節の中で、S、O、Cのどれかの役割を果たしています。
上の文でいえば、Oです。
上の文を2文に分ければ、
He knows the fact.
She is trying to conceal the fact.
となります。
もとの文を見ると、conceal の目的語がないことに気づきます。
だから、the fact が目的語であり、つまり that は関係代名詞なのです。
一方、接続詞の that は、文と文とを結ぶ役割を果たすものなので、SでもOでもCでもありません。
接続詞以外の役割を果たしません。
これが、
He knows the fact that she is trying to conceal the scandal.
のように、conceal の目的語が存在していれば、この that は「同格の that」です。
したがって、答はやはり(3)です。
難しいですね。
文法的な細かいところをついてくる問題です。
こんなことはわからなくても、英文が理解できれば、それでいいんじゃないの?
私も、そう思います。
それは、近年の英語教育の大きな流れでもあります。
大学入試共通テストは、読解力、しかもかなりの速読力を問う問題ばかりで、文法問題は出題されません。
私立大学の入試問題も、偏差値の高い大学の英文科や国際学科ほどこういう文法問題は少なく、時間内に大量の英文を読む入試問題に変わってきています。
時間内に大量の英文を読解してもらい、さらに、テーマを与えて、英文を書いてもらう。
それで十分に英語力は判断できます。
とはいえ、中堅私大は依然としてこういう出題がされますし、だから、模試にも出題されます。
理解しておいて損はない問題です。
問題 次の文の that と同じ働きの that を含む文を以下の(1)~(4)から選べ。
He coughed to give her the hint that she should leave the room.
(1) He couldn't make it clear that he had nothing to do with the accident.
(2) It was a dog that he caught in that mountain.
(3) He heard a rumor that wolves lived in that mountain.
(4) He knows the fact that she is trying to conceal.
色々な that があって、ちょっと難しいですね。
そもそも、一番上の問題文の that は、どういう that なのでしょうか。
この文は「その部屋を出るべきだというヒントを彼女に与えるために、彼は咳払いをした」という意味です。
He coughed という部分が、S(主語)とV(動詞)です。
その後ろは、副詞的用法の不定詞。「~するために」という意味です。
その不定詞の中で、また、V・O・Oという構造になっています。
give が不定詞の中でのV。
her が、不定詞の中でのO(目的語)。
the hint が、不定詞の中でのもう1つのO(目的語)です。
「誰々に」「何々を」の語順で、2つの目的語をもっている動詞ということです。
では、その後ろのthat 節は、何なのか?
これは、the hint の中身を説明しています。
どういうヒントであるのかを具体的に説明しているのです。
「彼女はその部屋を出るべきだ」というヒントです。
したがって、この that は、
the hint と she should leave the room を対等に結んでいます。
これを「同格の that」と呼びます。
接続詞 that の用法の1つです。
では、(1)~(4)で、同格の that はどれでしょうか。
1つ1つ見ていきましょう。
(1) He couldn't make it clear that he had nothing to do with the accident.
「彼は、その事故と関係がないことを明らかにすることができなかった」
この文は、同格の that ではないことは、比較的に簡単に見分けることができると思います。
He couldn't make it clear
までで、S・V・O・C です。
it は形式目的語。
目的語が長い内容なので、とりあえず it を立てて、Cを言ってから、ゆっくりと最後に it の中身を語っていく形の文です。
it =that he had nothing to do with the accident
です。
こういうのは「同格の that」とは言いません。
同格の that は、名詞の直後に置いてその名詞の中身を説明するもので、it のような代名詞の中身を説明するものではありません。
これも接続詞の that ではありますが、これは、真の目的語の that 節です。
(2) It was a dog that he caught in that mountain.
これは何でしょう?
「それは、彼が山の中で捕まえた犬だった」
という文でしょうか?
だとすれば、この that は、dog を修飾する関係代名詞の that です。
文脈によっては、そのような意味にとっても良いと思います。
あるいは、これは強調構文かもしれません。
it is ~ that で、強調したい内容を挟む、強調構文です。
そうだとすれば、
「彼がその山の中で捕まえたのは、犬だった」
となります。
いずれにせよ、「同格の that」ではありません。
(3) He heard a rumor that wolves lived in that mountain.
「彼は、オオカミがその山に住んでいるという噂を聞いた」という文です。
a rumor = wolves lived in that mountain
まさに、「同格の that」。
これが正解でしょう。
しかし、(4) を見て、「うん?」となる人は多いと思います。
(4) He knows the fact that she is trying to conceal.
「彼は、彼女が隠そうとしている事実を知っている」
これも「同格の that」なのではないか?
同格の that は、どんな名詞の後でも使用できるものではありません。
同格の that を使える名詞は限られていて、その名詞を覚えている人も多いと思います。
その中で、the fact that ~という用法は典型的なもので、例文でよく使われています。
では、(4) も同格の that なのでしょうか。
これが違うのです。
この that は、関係代名詞です。
ここで問題となるのが、
接続詞の that と、関係代名詞の that は、どう区別するか?
ということでしょう。
見分けは、それほど難しくありません。
関係代名詞の that は、その関係詞節の中で、S、O、Cのどれかの役割を果たしています。
上の文でいえば、Oです。
上の文を2文に分ければ、
He knows the fact.
She is trying to conceal the fact.
となります。
もとの文を見ると、conceal の目的語がないことに気づきます。
だから、the fact が目的語であり、つまり that は関係代名詞なのです。
一方、接続詞の that は、文と文とを結ぶ役割を果たすものなので、SでもOでもCでもありません。
接続詞以外の役割を果たしません。
これが、
He knows the fact that she is trying to conceal the scandal.
のように、conceal の目的語が存在していれば、この that は「同格の that」です。
したがって、答はやはり(3)です。
難しいですね。
文法的な細かいところをついてくる問題です。
こんなことはわからなくても、英文が理解できれば、それでいいんじゃないの?
私も、そう思います。
それは、近年の英語教育の大きな流れでもあります。
大学入試共通テストは、読解力、しかもかなりの速読力を問う問題ばかりで、文法問題は出題されません。
私立大学の入試問題も、偏差値の高い大学の英文科や国際学科ほどこういう文法問題は少なく、時間内に大量の英文を読む入試問題に変わってきています。
時間内に大量の英文を読解してもらい、さらに、テーマを与えて、英文を書いてもらう。
それで十分に英語力は判断できます。
とはいえ、中堅私大は依然としてこういう出題がされますし、だから、模試にも出題されます。
理解しておいて損はない問題です。
2022年09月04日
線分の比と面積の比。連比か分数か。
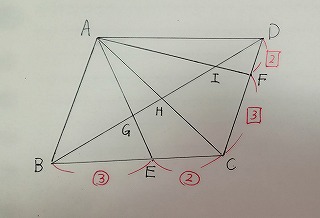
問題 図のように、平行四辺形ABCDがあり、BE : EC=CF : FD=3:2である。
対角線BDと線分AE、AC、AFとの交点をそれぞれG、H、Iとする。
(1) GH : HIの比を求めなさい。
(2) 四角形GECHと平行四辺形ABCDの面積比を求めなさい。
中3数学「相似」という単元の典型題ですが、受験算数でもおなじみの問題です。
おなじみのわりに、定着しない問題でもあります。
まずは受験算数らしく解いてみましょう。
(1)から。
GH : HIは、すぐに求められそうにありません。
これは、順を追って求めていかなければならない問題。
まずは、わかる比を書き込んでみましょう。
平行四辺形の対角線は、それぞれの中点で交わります。
すなわち、BH : HD=1:1
あとは?
図の中に相似な三角形があります。
「砂時計型」または「チョウチョ型」と呼ばれる、向かいあった相似の三角形が見えるでしょうか。
上下に位置しているものしか見えない、左右に位置しているものしか見えない、あるいはどちらも全く見えないなど、ここでも「目の癖」が大きな課題として立ちはだかってきます。
同じ問題を繰り返し解く、あるいは類題を沢山解くことで、見えるようにしていくことは可能です。
1組目は、△EGBと△AGD。
上下に羽を開いたチョウチョが見えます。
相似比は、3 : 5。
よって、対応する辺であるBG : DG=3 : 5 です。
もう1組。
左右に羽を広げるチョウチョが見えます。
△ABIと△FDI です。
相似比は、5 : 2。
よって、B I: DI=5 : 2 です。
ここまで、個々の線分の比を求めることまでは何とかできても、ここからどうしていいのかわからないという場合も多いです。
連比が組めないのです。
こんなときは、全体がいくつであるかで考えていきます。
最初の対角線で考えたときは、全体BDは1:1の合計ですから、2です。
次に△EGBと△AGDの相似で考えたときは、全体BDは、3 : 5の合計ですから、3+5=8です。
最後の△ABIと△FDIの相似で考えたときは、全体BDは、5 : 2の合計ですから、5+2=7です。
同じBDが、2であり、8であり、7である。
これを2と8と7の最小公倍数にそろえます。
56です。
全体BDを56として、比を直します。
BA : AD=28 : 28
BG : DG=3 : 5=21: 35
BI : DI=5 : 2=40 :16
比の1にあたる量が同じになるようにこれで整えることができました。
同じ比なので、足したり引いたりしても大丈夫です。
GH=BH-BG=28-21=7
HI=BI-BH=40-28=12
よって、求めるGH : HI=7 : 12 となります。
中学受験経験があるのに、この解き方が身についていない子は案外沢山います。
連比というと、例えば、AB : BC=2 : 3 , BC : CD=6 : 7 といったタイプの連比の解き方はマスターしていても、全体をそろえて比を整理していくことがあまり身についていなかったのだろうと思います。
だとすれば、比を使って解く方法には限界があります。
もう中学生になっているのであれば、こういう解き方はもう忘れていいのではないかと思います。
中学受験をしていない公立中学の生徒にこの「線分の比と面積の比」を教える場合、連比で教えようとしても基礎知識がないのでマスターはかなり困難であることが多いです。
「相似」を学習するのも生まれて初めて。
比を使った経験もあまりない。
そもそも、〇だ□だと、比の1にあたる量が異なるときには違う記号を用いて図に書き込みましょうと言っても、それが定着せず、すべてむきだしの数字を書き込んでしまう子のほうが多いのです。
比なのか実数なのかすら、よくわかりません。
比の1にあたる量が異なる比は区別しなければならないことがわかっていないふしがあります。
こちらの3:2と、あっちの3:2は同じであるとする、雑な考え方で比を扱ってしまいます。
それだけでなく、チョウチョ型の相似を発見することも、つい最近学習を始めたばかりなので、どこまでできるか心もとないのです。
平行四辺形の対角線がそれぞれの中点で交わるという中2で学習した知識も、見事に抜け落ちている場合もあります。
それだけ、こうした問題に対するハードルは高くなります。
中学受験を経験した生徒が、正答には至らないまでもとにかく何かやろうとしているのと比較すると、公立中学の生徒の答案はおおむね白紙です。
やはり、学習は相当遅れていると思わないわけにはいきません。
仕方ないです。
そんなに勉強しなくていい、楽しい小学生時代を満喫したのですから。
週4日、夕飯のお弁当を持って塾に通い続け、土日はテストを受けるか、親の徹底監督のもとで1日中勉強。
そんな経験を積んできた子たちよりも勉強が遅れているのは仕方ないと思います。
とはいえ、では中高一貫校の生徒が全員公立中学の生徒より学力は上かというと、そんなこともないのです。
中学入学後、びっくりするくらい勉強するのをやめてしまう私立中学の子たちもいます。
もうゴールテープを切ったと誤解しているのか、あるいは、もう余力はなく、燃え尽きてしまったのか。
中学の数学はあまり理解していないし、受験算数は錆びついているし、こりゃあ大変だという私立の生徒はたくさんいます。
一方、公立中学の生徒で、中学生になってからしっかり勉強するようになり、頭角を表してくる子たちは、中学生になっている分だけ小学生よりも脳が発達していて思考が複雑ですから、一気に飛躍していくことができます。
どちらの道を選んでも、利点は勿論ある一方、それに伴う困難もあるのだと思います。
学問に王道なしは、やはり本当のことなのでしょう。
これだけが正解という道はないのだと思うのです。
では、中学生ならば、どう解くのか。
今更、連比のマスターなど不要です。
すべて分数で処理していけばいいのです。
小学生は、分数に対する理解が脳の発達上追いついていかない子が多いので、何でも整数に直して考えるのです。
しかし、中学生ならば、分数で処理していけます。
つまり、比ではなく、割合でみていきます。
比と割合は本質は同じものですが、割合ならば、常に全体が1です。
直接、比較できるし、たし算も引き算もできるのです。
途中までの考え方は同じです。
平行四辺形の対角線はそれぞれの中点で交わるので、
BH=1/2BD
△EGBと△AGDの相似より、BG=3/8BD
△ABIと△FDIの相似より、BI=5/7BD
よって、
GH=BH-BG=1/2BD-3/8BD=1/8BD
HI=BI-BH=5/7BD-1/2BD=3/14BD
よって、
GH : HI=1/8 : 3/14=7 : 12
となります。
次の問題。
(2) 四角形GECHと平行四辺形ABCDの面積比を求めなさい。
相似な四角形というのは、問題にはほとんど出てきません。
四角形同士の面積は比べにくいです。
基本は三角形で比べるということをまず認識しておくと、解きやすくなります。
四角形GECHは、三角形から三角形を引いた残りとして考えられないだろうかという発想で図を見ます。
△BHC-△BGE で求められます。
ここで、底辺が一直線上にあり、高さの比も底辺と垂直ではなくても一直線上で見ることができれば、
(三角形の面積の比)=(底辺の比)×(高さの比)
で求めることができるという知識があれば、簡単に解くことができます。
「比の積」「比の商」は、受験算数でも難しい単元で、身につかない子が多いです。
1にあたる量が異なる比は足したらダメ、引いたらダメと散々言われてきたのに、突然かけ算とわり算はOKと言われても、そりゃあ理解を超えていますよね。
ここがピンとくる子と、何を言っているのが全然わからない子とで、こうした問題が解けるか解けないか、大差がついていきます。
ともあれ、△BHCと△BGEは、
底辺の比が、5 : 3
高さの比が、4 : 3
よって、面積の比は、20 : 9 です。
ということは、
四角形GECH=△BHC-△BGE=11/20△BHC
さらに、△BHC=1/4平行四辺形ABCDですから、
四角形GECH=11/20×1/4平行四辺形ABCD=11/80平行四辺形ABCD
よって、四角形GECHと平行四辺形ABCDの面積比は、11:80 です。
これも、小学生ならば、
△BHCと△BGE=20:9 がわかったところで、
四角形GECHは20-9=11
平行四辺形ABCDは、20×4=80
と求めることで、 11:80 という正解に至ります。
対角線BDと線分AE、AC、AFとの交点をそれぞれG、H、Iとする。
(1) GH : HIの比を求めなさい。
(2) 四角形GECHと平行四辺形ABCDの面積比を求めなさい。
中3数学「相似」という単元の典型題ですが、受験算数でもおなじみの問題です。
おなじみのわりに、定着しない問題でもあります。
まずは受験算数らしく解いてみましょう。
(1)から。
GH : HIは、すぐに求められそうにありません。
これは、順を追って求めていかなければならない問題。
まずは、わかる比を書き込んでみましょう。
平行四辺形の対角線は、それぞれの中点で交わります。
すなわち、BH : HD=1:1
あとは?
図の中に相似な三角形があります。
「砂時計型」または「チョウチョ型」と呼ばれる、向かいあった相似の三角形が見えるでしょうか。
上下に位置しているものしか見えない、左右に位置しているものしか見えない、あるいはどちらも全く見えないなど、ここでも「目の癖」が大きな課題として立ちはだかってきます。
同じ問題を繰り返し解く、あるいは類題を沢山解くことで、見えるようにしていくことは可能です。
1組目は、△EGBと△AGD。
上下に羽を開いたチョウチョが見えます。
相似比は、3 : 5。
よって、対応する辺であるBG : DG=3 : 5 です。
もう1組。
左右に羽を広げるチョウチョが見えます。
△ABIと△FDI です。
相似比は、5 : 2。
よって、B I: DI=5 : 2 です。
ここまで、個々の線分の比を求めることまでは何とかできても、ここからどうしていいのかわからないという場合も多いです。
連比が組めないのです。
こんなときは、全体がいくつであるかで考えていきます。
最初の対角線で考えたときは、全体BDは1:1の合計ですから、2です。
次に△EGBと△AGDの相似で考えたときは、全体BDは、3 : 5の合計ですから、3+5=8です。
最後の△ABIと△FDIの相似で考えたときは、全体BDは、5 : 2の合計ですから、5+2=7です。
同じBDが、2であり、8であり、7である。
これを2と8と7の最小公倍数にそろえます。
56です。
全体BDを56として、比を直します。
BA : AD=28 : 28
BG : DG=3 : 5=21: 35
BI : DI=5 : 2=40 :16
比の1にあたる量が同じになるようにこれで整えることができました。
同じ比なので、足したり引いたりしても大丈夫です。
GH=BH-BG=28-21=7
HI=BI-BH=40-28=12
よって、求めるGH : HI=7 : 12 となります。
中学受験経験があるのに、この解き方が身についていない子は案外沢山います。
連比というと、例えば、AB : BC=2 : 3 , BC : CD=6 : 7 といったタイプの連比の解き方はマスターしていても、全体をそろえて比を整理していくことがあまり身についていなかったのだろうと思います。
だとすれば、比を使って解く方法には限界があります。
もう中学生になっているのであれば、こういう解き方はもう忘れていいのではないかと思います。
中学受験をしていない公立中学の生徒にこの「線分の比と面積の比」を教える場合、連比で教えようとしても基礎知識がないのでマスターはかなり困難であることが多いです。
「相似」を学習するのも生まれて初めて。
比を使った経験もあまりない。
そもそも、〇だ□だと、比の1にあたる量が異なるときには違う記号を用いて図に書き込みましょうと言っても、それが定着せず、すべてむきだしの数字を書き込んでしまう子のほうが多いのです。
比なのか実数なのかすら、よくわかりません。
比の1にあたる量が異なる比は区別しなければならないことがわかっていないふしがあります。
こちらの3:2と、あっちの3:2は同じであるとする、雑な考え方で比を扱ってしまいます。
それだけでなく、チョウチョ型の相似を発見することも、つい最近学習を始めたばかりなので、どこまでできるか心もとないのです。
平行四辺形の対角線がそれぞれの中点で交わるという中2で学習した知識も、見事に抜け落ちている場合もあります。
それだけ、こうした問題に対するハードルは高くなります。
中学受験を経験した生徒が、正答には至らないまでもとにかく何かやろうとしているのと比較すると、公立中学の生徒の答案はおおむね白紙です。
やはり、学習は相当遅れていると思わないわけにはいきません。
仕方ないです。
そんなに勉強しなくていい、楽しい小学生時代を満喫したのですから。
週4日、夕飯のお弁当を持って塾に通い続け、土日はテストを受けるか、親の徹底監督のもとで1日中勉強。
そんな経験を積んできた子たちよりも勉強が遅れているのは仕方ないと思います。
とはいえ、では中高一貫校の生徒が全員公立中学の生徒より学力は上かというと、そんなこともないのです。
中学入学後、びっくりするくらい勉強するのをやめてしまう私立中学の子たちもいます。
もうゴールテープを切ったと誤解しているのか、あるいは、もう余力はなく、燃え尽きてしまったのか。
中学の数学はあまり理解していないし、受験算数は錆びついているし、こりゃあ大変だという私立の生徒はたくさんいます。
一方、公立中学の生徒で、中学生になってからしっかり勉強するようになり、頭角を表してくる子たちは、中学生になっている分だけ小学生よりも脳が発達していて思考が複雑ですから、一気に飛躍していくことができます。
どちらの道を選んでも、利点は勿論ある一方、それに伴う困難もあるのだと思います。
学問に王道なしは、やはり本当のことなのでしょう。
これだけが正解という道はないのだと思うのです。
では、中学生ならば、どう解くのか。
今更、連比のマスターなど不要です。
すべて分数で処理していけばいいのです。
小学生は、分数に対する理解が脳の発達上追いついていかない子が多いので、何でも整数に直して考えるのです。
しかし、中学生ならば、分数で処理していけます。
つまり、比ではなく、割合でみていきます。
比と割合は本質は同じものですが、割合ならば、常に全体が1です。
直接、比較できるし、たし算も引き算もできるのです。
途中までの考え方は同じです。
平行四辺形の対角線はそれぞれの中点で交わるので、
BH=1/2BD
△EGBと△AGDの相似より、BG=3/8BD
△ABIと△FDIの相似より、BI=5/7BD
よって、
GH=BH-BG=1/2BD-3/8BD=1/8BD
HI=BI-BH=5/7BD-1/2BD=3/14BD
よって、
GH : HI=1/8 : 3/14=7 : 12
となります。
次の問題。
(2) 四角形GECHと平行四辺形ABCDの面積比を求めなさい。
相似な四角形というのは、問題にはほとんど出てきません。
四角形同士の面積は比べにくいです。
基本は三角形で比べるということをまず認識しておくと、解きやすくなります。
四角形GECHは、三角形から三角形を引いた残りとして考えられないだろうかという発想で図を見ます。
△BHC-△BGE で求められます。
ここで、底辺が一直線上にあり、高さの比も底辺と垂直ではなくても一直線上で見ることができれば、
(三角形の面積の比)=(底辺の比)×(高さの比)
で求めることができるという知識があれば、簡単に解くことができます。
「比の積」「比の商」は、受験算数でも難しい単元で、身につかない子が多いです。
1にあたる量が異なる比は足したらダメ、引いたらダメと散々言われてきたのに、突然かけ算とわり算はOKと言われても、そりゃあ理解を超えていますよね。
ここがピンとくる子と、何を言っているのが全然わからない子とで、こうした問題が解けるか解けないか、大差がついていきます。
ともあれ、△BHCと△BGEは、
底辺の比が、5 : 3
高さの比が、4 : 3
よって、面積の比は、20 : 9 です。
ということは、
四角形GECH=△BHC-△BGE=11/20△BHC
さらに、△BHC=1/4平行四辺形ABCDですから、
四角形GECH=11/20×1/4平行四辺形ABCD=11/80平行四辺形ABCD
よって、四角形GECHと平行四辺形ABCDの面積比は、11:80 です。
これも、小学生ならば、
△BHCと△BGE=20:9 がわかったところで、
四角形GECHは20-9=11
平行四辺形ABCDは、20×4=80
と求めることで、 11:80 という正解に至ります。





















