2024年07月04日
「三か月でマスターする数学」は興味深い番組です。
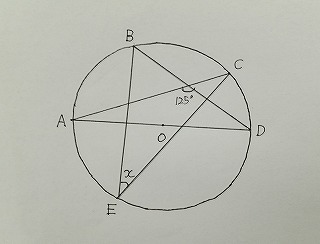
問題 上の図の x の角の大きさを求めよ。
NHK Eテレで「三か月でマスターする数学」という番組が7月から始まりました。
この種の数学番組は、大学数学を扱うことが多いのですが、この番組は、中3の数学から始まりました。
第1回は「円周角の定理」。
数学が苦手な女性アナウンサーに、講師が数学を教えるという形で番組は進行します。
この設定がまず興味深いです。
数学が苦手な子は、数学に対して寡黙です。
「何がわからない?」
と尋ねても、返答がないことがあります。
私が板書を指さしながら、
「この行はわかる?ここは?」
と1行1行確認しようとしても、パニックを起こしているのか、私のそうした意図を察してくれず返答がないことすらあります。
気持ちを落ち着かせ、私の意図を理解してもらい、1行1行、どこがわからないのかを確認していく。
それが私の仕事です。
数学は苦手なのだが、コメント力のある生徒。
これは、数学を教える者から見ると、理想の生徒です。
何がわからないから、数学がわからないのか。
私が知りたいのは、まさにそれです。
しかし、番組は私の予想外の方向に進んでいきました。
番組前半、基本の解説が行われました。
等しい弧の円周角は等しい。
特に、半円の弧の円周角は90度である。
そして、練習問題を解くことになりました。
それが、上の問題です。
数学が苦手なアナウンサーは、やはり、解くことができません。
そこで、講師からヒントが出されました。
「補助線を引いてみましょう」
上の図に戻ってください。
この問題、補助線を1本入れれば、かなりわかりやすくなります。
どこに補助線を入れたらいいでしょうか?
ここで、アナウンサーが入れた補助線は、線分BCでした。
私は天を仰ぎました。
そうだ。
そうなんですよ。
図形が苦手な人は、そうなんですよね。
いや、この番組は、台本があってのことで、そのアナウンサーは狂言回しで、わざとやっているのかもしれませんが、怖いくらいの既視感でした。
そのとき、しかし、講師の人は、こちらのほうがいいですよと、さっさとABに補助線を入れました。
講師の助言を受け、上手く誘導されて、アナウンサーは、そのままやがて正解にたどりつき、満足そうでした。
台本ではなく、本気で満足しているようだと感じるほどに。
そこで、私は再度天を仰いでしまったのでした。
この番組は、大人が数学を少し楽しむ番組だから、それでいいのです。
中学の数学は、今やり直せば案外いけるかも、と思う気持ちが大切。
数学に抵抗感がなくなることが大切。
番組の趣旨はそうなのですが、私の仕事はそうではありません。
生徒に数学のテストで良い点を取ってもらうこと。
目標は、その一点に絞られています。
数学が好きになって、それで得点も上がるなら、それは何より。
ただ、数学は特に好きにはならなくても、得点が上がるのならば、それでもいいのです。
人は、自分が上手くできることには好感を抱くものなので、得点が上がれば今までほどの嫌悪感はなくなります。
得点が上がるのが先でも構わないのです。
つまりは、自力で問題に正解できることが大切。
そして、その観点でこの番組を見ると、感じるのです。
このアナウンサーは、わかったつもりにはなっているが、類題を自力で解くことはできないでしょう。
なぜか?
有効な補助線を入れることが自力でできないからです。
類題ではまた、問題を解く最初の一歩でつまずくでしょう。
そして、図形問題が苦手な人の多くが、そうなのです。
もう一度、上の図に戻ってください。
アナウンサーは、線分BCを補助線として入れたのです。
・・・何で、そこに補助線を入れるかなあ?
でも、図形が苦手な子は、確かに、線分BCのような、あまり役に立たない補助線を入れることが多いのです。
予想外のところに補助線を入れます。
何でなのかなあ?
図形の問題が自力で解けないというのは、結局、そこなのです。
BCに補助線を入れていては、この問題は解けないのです。
そして、番組の講師は、補助線はなぜBCではなくABなのかについては解説せず、そこはさっと通り過ぎて、アナウンサーが自力で解いているかのような雰囲気を作っていました。
正しい補助線を自力で入れられない限り、テストで類題は解けないのですが。
学校や塾の集団授業はしっかり聞いているのに、数学の成績が上がらない・・・。
評判のいい数学動画を見て、理解した気がするのに、数学の成績が上がらない・・・。
その理由をあえて描いているような番組でした。
私は、図形に特別な才能を持っているわけではないので、上のような問題を見たときに、一瞬で最後まで解法を見通すことはできません。
先は見えないまま、とりあえず補助線を入れてみるのが常です。
番組を見ていたときも、そうでした。
補助線は線分ABだなあとテレビ画面を見ながらぼんやり思っていました。
それは、勘です。
長年、この種の問題は沢山解いていますから、経験の多さから勘が働きます。
しかし、勘ではダメです。
生徒に教えるならば、そこを理論化しなければなりません。
補助線はどう入れるのか。
補助線の入れ方の原則。
①結ばれていない点と点とを結ぶ。
②既に存在する線分を延長させる。
③既に存在する線分と平行な線を引く。
④既に存在する線分に垂線を下ろす。
勘で解けないのならば、理屈で解く。
そうはいっても、結ばれていない点と点とを結ぶのならば、線分BCも、そうなのです。
なぜ、線分BCを真っ先に思いついてしまうのか。
数学が苦手だけれどコメント力のあるアナウンサーには、そこを語ってほしかった。
なぜBCに補助線を入れたのか。
どういう考えでそうしてしまうのか。
私が知りたいのは、そこなのです。
線分BCを書き込んで、△BCEを作っても、それでは図は動きません。
それが x の角に一番関係があると思って書き込んでしまうのでしょうか。
そこに対して自覚的になれば、自分の思考の癖に気づくことができます。
それが改善への道です。
シンプルに、x の角を円周角の定理でどこかに移したいな、という発想だけでも、補助線はABが有力です。
さらに言えば、直前に、半円の弧の円周角は90度と学習したばかりなのだから、どうせ作るならば直角三角形を作りましょう。
円周角の問題は、直角三角形が作れるのならば、作る。
図中に円の直径が描かれているのならば、必ず直角三角形が作れます。
それが鉄則。
しかし、そう指示すると、今度は、頂点Bから直径ADに垂線を下ろす、という荒業を繰り広げる子もいます。
円周角を学習したのだから、それを活かすことを考えよう。
半円の弧の円周角は90度であることを、どこかで使えないか。
そういう発想で問題に向かえば、有効な補助線を引けるはずなのですが、図形が苦手な子は、学習したことを、それはそれとして、問題を解くときにはポンと脇に置いてしまいます。
学んだことを使って問題を解くという発想がない。
そこが脳の中で繋がっていないように感じます。
わかったつもりになっただけでは、実際の問題は解けません。
自分で解いて、間違えて。
正解を知って、そこから重要なことを吸収して。
その繰り返しで、図形問題への「勘」「センス」は養われます。
生徒たちの「予想外の補助線」と格闘し、何でそんなところに補助線を入れたいのか、その傾向を分析し、そこへの経路を塞ぎ、何とか類題でも正解できるように経験値を高めていく。
それが私の仕事です。
最後に、上の問題の解答を。
上の図を書き写して、補助線ABを入れてください。
弧BCに対する円周角は等しいから、∠BEC=∠BAC。
すなわち、∠BAC=x です。
また、線分ADはこの円の直径ですから、∠ABDは、半円の弧の円周角。
すなわち、∠ABD=90°
ここで、△ABDだけに目を奪われないことがコツです。
ここも、生徒が苦手とするところです。
着目する三角形が頭の中で固定され、そこから離脱できないことがありますが、乗り換えていくのが図形問題の常。
ACとBDの交点、125°のところの点を点Fとし、新しく△ABFに着目します。
∠BAF=x
∠ABF=90°
そして、∠AFBは、125°のところの外角ですから、
180-125=55 で、
∠AFB=55°
三角形の内角の和は180°ですから、求める角xは、
180-90-55=35
x=35 です。
NHK Eテレで「三か月でマスターする数学」という番組が7月から始まりました。
この種の数学番組は、大学数学を扱うことが多いのですが、この番組は、中3の数学から始まりました。
第1回は「円周角の定理」。
数学が苦手な女性アナウンサーに、講師が数学を教えるという形で番組は進行します。
この設定がまず興味深いです。
数学が苦手な子は、数学に対して寡黙です。
「何がわからない?」
と尋ねても、返答がないことがあります。
私が板書を指さしながら、
「この行はわかる?ここは?」
と1行1行確認しようとしても、パニックを起こしているのか、私のそうした意図を察してくれず返答がないことすらあります。
気持ちを落ち着かせ、私の意図を理解してもらい、1行1行、どこがわからないのかを確認していく。
それが私の仕事です。
数学は苦手なのだが、コメント力のある生徒。
これは、数学を教える者から見ると、理想の生徒です。
何がわからないから、数学がわからないのか。
私が知りたいのは、まさにそれです。
しかし、番組は私の予想外の方向に進んでいきました。
番組前半、基本の解説が行われました。
等しい弧の円周角は等しい。
特に、半円の弧の円周角は90度である。
そして、練習問題を解くことになりました。
それが、上の問題です。
数学が苦手なアナウンサーは、やはり、解くことができません。
そこで、講師からヒントが出されました。
「補助線を引いてみましょう」
上の図に戻ってください。
この問題、補助線を1本入れれば、かなりわかりやすくなります。
どこに補助線を入れたらいいでしょうか?
ここで、アナウンサーが入れた補助線は、線分BCでした。
私は天を仰ぎました。
そうだ。
そうなんですよ。
図形が苦手な人は、そうなんですよね。
いや、この番組は、台本があってのことで、そのアナウンサーは狂言回しで、わざとやっているのかもしれませんが、怖いくらいの既視感でした。
そのとき、しかし、講師の人は、こちらのほうがいいですよと、さっさとABに補助線を入れました。
講師の助言を受け、上手く誘導されて、アナウンサーは、そのままやがて正解にたどりつき、満足そうでした。
台本ではなく、本気で満足しているようだと感じるほどに。
そこで、私は再度天を仰いでしまったのでした。
この番組は、大人が数学を少し楽しむ番組だから、それでいいのです。
中学の数学は、今やり直せば案外いけるかも、と思う気持ちが大切。
数学に抵抗感がなくなることが大切。
番組の趣旨はそうなのですが、私の仕事はそうではありません。
生徒に数学のテストで良い点を取ってもらうこと。
目標は、その一点に絞られています。
数学が好きになって、それで得点も上がるなら、それは何より。
ただ、数学は特に好きにはならなくても、得点が上がるのならば、それでもいいのです。
人は、自分が上手くできることには好感を抱くものなので、得点が上がれば今までほどの嫌悪感はなくなります。
得点が上がるのが先でも構わないのです。
つまりは、自力で問題に正解できることが大切。
そして、その観点でこの番組を見ると、感じるのです。
このアナウンサーは、わかったつもりにはなっているが、類題を自力で解くことはできないでしょう。
なぜか?
有効な補助線を入れることが自力でできないからです。
類題ではまた、問題を解く最初の一歩でつまずくでしょう。
そして、図形問題が苦手な人の多くが、そうなのです。
もう一度、上の図に戻ってください。
アナウンサーは、線分BCを補助線として入れたのです。
・・・何で、そこに補助線を入れるかなあ?
でも、図形が苦手な子は、確かに、線分BCのような、あまり役に立たない補助線を入れることが多いのです。
予想外のところに補助線を入れます。
何でなのかなあ?
図形の問題が自力で解けないというのは、結局、そこなのです。
BCに補助線を入れていては、この問題は解けないのです。
そして、番組の講師は、補助線はなぜBCではなくABなのかについては解説せず、そこはさっと通り過ぎて、アナウンサーが自力で解いているかのような雰囲気を作っていました。
正しい補助線を自力で入れられない限り、テストで類題は解けないのですが。
学校や塾の集団授業はしっかり聞いているのに、数学の成績が上がらない・・・。
評判のいい数学動画を見て、理解した気がするのに、数学の成績が上がらない・・・。
その理由をあえて描いているような番組でした。
私は、図形に特別な才能を持っているわけではないので、上のような問題を見たときに、一瞬で最後まで解法を見通すことはできません。
先は見えないまま、とりあえず補助線を入れてみるのが常です。
番組を見ていたときも、そうでした。
補助線は線分ABだなあとテレビ画面を見ながらぼんやり思っていました。
それは、勘です。
長年、この種の問題は沢山解いていますから、経験の多さから勘が働きます。
しかし、勘ではダメです。
生徒に教えるならば、そこを理論化しなければなりません。
補助線はどう入れるのか。
補助線の入れ方の原則。
①結ばれていない点と点とを結ぶ。
②既に存在する線分を延長させる。
③既に存在する線分と平行な線を引く。
④既に存在する線分に垂線を下ろす。
勘で解けないのならば、理屈で解く。
そうはいっても、結ばれていない点と点とを結ぶのならば、線分BCも、そうなのです。
なぜ、線分BCを真っ先に思いついてしまうのか。
数学が苦手だけれどコメント力のあるアナウンサーには、そこを語ってほしかった。
なぜBCに補助線を入れたのか。
どういう考えでそうしてしまうのか。
私が知りたいのは、そこなのです。
線分BCを書き込んで、△BCEを作っても、それでは図は動きません。
それが x の角に一番関係があると思って書き込んでしまうのでしょうか。
そこに対して自覚的になれば、自分の思考の癖に気づくことができます。
それが改善への道です。
シンプルに、x の角を円周角の定理でどこかに移したいな、という発想だけでも、補助線はABが有力です。
さらに言えば、直前に、半円の弧の円周角は90度と学習したばかりなのだから、どうせ作るならば直角三角形を作りましょう。
円周角の問題は、直角三角形が作れるのならば、作る。
図中に円の直径が描かれているのならば、必ず直角三角形が作れます。
それが鉄則。
しかし、そう指示すると、今度は、頂点Bから直径ADに垂線を下ろす、という荒業を繰り広げる子もいます。
円周角を学習したのだから、それを活かすことを考えよう。
半円の弧の円周角は90度であることを、どこかで使えないか。
そういう発想で問題に向かえば、有効な補助線を引けるはずなのですが、図形が苦手な子は、学習したことを、それはそれとして、問題を解くときにはポンと脇に置いてしまいます。
学んだことを使って問題を解くという発想がない。
そこが脳の中で繋がっていないように感じます。
わかったつもりになっただけでは、実際の問題は解けません。
自分で解いて、間違えて。
正解を知って、そこから重要なことを吸収して。
その繰り返しで、図形問題への「勘」「センス」は養われます。
生徒たちの「予想外の補助線」と格闘し、何でそんなところに補助線を入れたいのか、その傾向を分析し、そこへの経路を塞ぎ、何とか類題でも正解できるように経験値を高めていく。
それが私の仕事です。
最後に、上の問題の解答を。
上の図を書き写して、補助線ABを入れてください。
弧BCに対する円周角は等しいから、∠BEC=∠BAC。
すなわち、∠BAC=x です。
また、線分ADはこの円の直径ですから、∠ABDは、半円の弧の円周角。
すなわち、∠ABD=90°
ここで、△ABDだけに目を奪われないことがコツです。
ここも、生徒が苦手とするところです。
着目する三角形が頭の中で固定され、そこから離脱できないことがありますが、乗り換えていくのが図形問題の常。
ACとBDの交点、125°のところの点を点Fとし、新しく△ABFに着目します。
∠BAF=x
∠ABF=90°
そして、∠AFBは、125°のところの外角ですから、
180-125=55 で、
∠AFB=55°
三角形の内角の和は180°ですから、求める角xは、
180-90-55=35
x=35 です。
Posted by セギ at 12:47│Comments(0)
※このブログではブログの持ち主が承認した後、コメントが反映される設定です。





















