
お知らせ
2025年03月27日
中学数学。1次方程式の利用。中級。速さに関する問題。

画像は、井の頭公園の、ニリンソウです。
さて、まずは、こんな問題から。
1次方程式の問題です。
問題1
午前8時に、3㎞離れた学校へ兄が出かけ、兄が出発してから6分後に妹が走って同じ道を追いかけた。兄が歩く速さが分速80m、妹が走る速さが分速120mであるとき、妹が兄に追いつく時刻を求めなさい。
基本が身についている人にとっては、何とか立式できるレベルの問題です。
公立中学で使う普通の教科書にも載っている問題です。
まず、何を x とおくか。
「時刻を x とおく」とうっかり書いてしまうことがあるかもしれませんが、時刻と時間は違うのです。
、
時刻と時間。
小学校の低学年で学習している内容ですが、こういう根本の概念ほど、言葉で説明しようとするとむしろ難しいことがあります。
「今の時刻は、午後12時58分と」いうのが、時刻。
「家から学校まで30分かかる」というのが時間。
10歳未満の子どものほうが、むしろ、こうした概念を概念のまますっと理解できるのですが、そのときに学び損ねると、一生わからない・・・ということも起こります。
いくら言葉を重ねて説明しても、わからないものはわからないようなのです・・・。
それはともかく。
時刻を x とするのは、不可能ではないです。
その場合、上の問題ならば、「午前8時 x 分とする」ことになるのですが、この処理は案外厄介なので、時間を x で表したほうがスッキリすると思います。
すなわち、答案の1行目は、
「兄が x 分歩くとする」
しかし、この1行目を書き忘れる人は多いです。
あるとき、テスト直しノートを提出させる熱心な学校の先生に教わっている中学生がいました。
しかし、返却されたノートには、「?」「何で?」「どういう意味?」などの赤ペンの文字が入っていて、評価は「B」でした。
しっかり直したつもりなのに、なぜ「A」ではないのか?
テスト直しノートをどう直していいかわからない・・・。
そういう悩みを聞いて、そのテスト直しノートを見てみると、何を x とするのか書いていませんでした。
そのことに気づかず、次のテスト直しでは、もっと詳しく説明しなければいけないと思ったのか、変な方向に詳しく、文章題を線分図に表してみたり、カラフルに色ペンを使ったりしていました。
何を x とするかは必ず書きなさいと、方程式の利用の学習の間、毎回、毎回、助言したのに、何で身につかないのだろう・・・。
そして、学校の先生も、テスト直しノートに赤ペンで書き込むなら、
「何が x?」
と端的に書いたほうが伝わるのに・・・。
中学一年生は、本当に、まだ小学生の尻尾が残っている子が多く、「〇〇をxとする」といった日本語が数学の答案に必要だということが、どうしても信じられないようなのです。
だから、注意されても、すぐ忘れます。
数学は、式と答だけ書けばいいんだ、という小学生の「尻尾」が生えたままなのです。
また余談にそれてしまいました・・・。
そろそろ、問1の方程式を立てましょう。
もう一度、問題を見てください。
問題1
午前8時に、3㎞離れた学校へ兄が出かけ、兄が出発してから6分後に妹が走って同じ道を追いかけた。兄が歩く速さが分速80m、妹が走る速さが分速120mであるとき、妹が兄に追いつく時刻を求めなさい。
兄がx分歩くとする。
そうすると、妹は遅れて出発していますから、妹の時間は、(X-6)分です。
速さは問題文に書いてあるし、時間はxを使って表せます。
これは、方程式は、道のりを表すものを作ればいいですね。
追いつくまでの兄の道のりと妹の道のりは等しいです。
速さ×時間=道のり ですから、
80x=120(x-6)
これを解いて、x=18
さて、ここから時刻に直す必要があります。
兄が出発した時刻が午前8時。
そこから18分歩いたのですから、
解答は、午前8時18分です。
問題2
弟は分速73mで歩いて、家から1.7㎞離れた駅に向かって出発した。弟が出発してから15分後に姉が自転車に乗って同じ道を分速292mで弟を追いかけた。姉は弟に駅まであと何mのところで追いつくか答えなさい。
さて、方程式の文章題は、基本は求めたいものを x としますが、この問題、「駅まであと x mのところで追いつくとする」としてしまうと、式が難しくなりそうな嫌な予感がします。
方程式は、わり算の式よりも、かけ算の式を立てたほうが簡単です。
どうしてもわり算、すなわち分数の式しか立てられないこともあるけれど、今回はそうではなさそう。
そういう判断ができると、この問題は楽に解けます
これも、やはり、「姉が x 分走るとする」のほうが、速さ×時間=道のり の、簡単な式を立てられそうです。
姉が x 分走るとする。
そうすると、弟は姉よりも前に出発していますから、弟の時間は(15+x)分。
弟の道のり=姉の道のり ですから。
292x=75(15+x)
これを解いて、
x=5
姉が5分走ったことがわかりました。
では、姉の道のりは、
292×5=1460
駅までは1.7㎞=1700mですから、残りの道のりは、
1700-1460=240
答えは、240mです。
問題3
9㎞離れたところへ行くのに、はしめは時速5㎞で歩き、途中から時速3㎞で歩いたら、2時間かかった。時速5㎞で歩いた道のりを求めなさい。
よし、これは、前半の歩いた道のりを x とするので大丈夫でしょう。
方程式は、時間を表す式を立てましょう。
時速5kmで歩いた道のりを x ㎞とする。
道のりは全部で9㎞ですから、時速3㎞で歩いた道のりは、(9-x)㎞ と表すことができます。
前半の時間は、x / 5 時間。
後半の時間は、(9-x) / 3 時間。
その合計が2時間なのだから、
x / 5 +(9-x) / 3=2
これを解いて、
x=15 / 2
解答は、15 / 2㎞。
問題4
AとBが5㎞離れた場所にいる。Aは午前9時に、Bは午前9時2分に互いに向かって走り出した。Aが分速250m、Bが分速200mで走るとき、2人が出会う時刻を求めなさい。
Aが出発したのが午前9時でわかりやすいので、Aの走る時間をx分としましょう。
Bは出発が2分遅かったので、走る時間は(x-2)分となります。
今回、2人の道のりは異なります。
しかし、2人で協力して5㎞走ったのですから、2人の道のりの和が5㎞=5000mです。
Aの走る時間を x 分とする。
250x+200(x-2)=5000
これを解いて、
x=12
解答は、午前9時12分 です。
さて、ここまで逐一ヒントを出しながら、生徒と一緒に立式し、上の問題1から4まで解いたときのことです。
生徒から、言われました。
「・・・わからない」
「うん?何がわからない?」
「解いたのを見ればわかるけど、自分では式が立てられない・・・」
・・・なるほど。
「どういうところがわからない?」
ここで、長い長い沈黙がありました。
でも、何か言ってくれないと、何がどうわからないのか、私もわからないので、何か喋り出すまで、辛抱強く待ちました。
ついに、その子は口を開きました。
「・・・式の形が・・・」
「うん?」
「・・・式の形が同じじゃない」
「・・・?」
式を見直してみましょう。
問題1は、
80x=120(x-6)
問題2は、
73(15+x)=292x
問題3は、
x / 5 +(9-x) / 3=2
問題4は、
250x+200(x-2)=5000
「・・・特にどこが違うと思う?」
そう問いかけてみました。
「たすだったり、引くだったりするのが、・・・」
「たすだったり、引くだったり?どこのところが?」
「・・・x-6だったり、15+xだったり、9-xだったりするのが、わからない・・・」
「・・・」
・・・問題によって、たすだったり引くだったりするのは、当たり前じゃないの?
同じ問題じゃないんだから・・・。
心の中でそう思い、そして気づきました。
そうか。
この子は、全部たし算ならたし算、ひき算ならひき算であってほしいのか・・・。
式の形が、いつも全部同じであってほしいのか・・・。
その式の形さえ覚えれば良いという勉強がしたいのか・・・。
気持ちはわかるのです。
しかし、そういうパターン把握で方程式の文章題をこなせると夢を見ている間は、方程式の文章題は自分で解けるようにはならないのです。
文章を読んで、意味を理解して、構造を把握して、その都度関係をつかんで、式を立てる。
そういう「まっとうな解き方」が実は正解への最短距離なのですが、なぜか、それだけは絶対にしない、そんなことは許容しないという子たちがいます。
おそらく、小学生の頃から、算数の文章題を意味を読み取って式を立てることは、一切してこなかったのだと思います。
すべてパータン把握でこなしてきた。
小学校では、それでそこそこ大丈夫だった。
ときどき、「単位量あたり」とか、「割合」とか「速さ」とか、上手くいかない単元もあったけれど、そういうのは終わってしまえば、もう過去のこと。
これからも、自分はこのやり方でいく。
だって、このやり方しかわからない。
パターンがあるはずだ。
それを教えて!
ある種、背筋が寒くなるのは、こういうときです。
気持ちはわかるのですが、文章題に取り組む姿勢が、根本的に間違っているのです。
問題文を読んで、読解して、構造を把握するから、立式できるのです。
ただ、それを身につけるには、時間がかかります。
何年も何年もかかります。
だから、小学校の簡単な算数から、文章題で少しずつ練習して能力を伸ばしてきたはずなのに、小学校の頃はあまりにも簡単だったから、文章を読まずに式を立ててきた子が、今の時代、ますます増えているように感じます。
文章題にある程度対応できる子と、全く対応できない子に、はっきりと分かれます。
簡単な文章だった小学生時代に読み方を身につけなかったので、中学の数学になると、文章の構造をもう読み取れない・・・。
でも、今からでも遅くないのです。
文章を読んで、意味を理解することは、学問の基本です。
文章を読み取る必要があるのだと、本人が理解してくれれば、そこから先に進めます。
怖いのは、文章を読み取る方向に本人の気持ちが一切向かない場合です。
何かパターンがあるはずだ。
絶対あるはずだ。
そういう抜け道があるはずだ。
この先生は、それがわかっていないだけだ。
どこかに、抜け道があるんだ・・・。
いつまでもそう考えて、文章と向き合えないのです。
私は、「文章が読めない」ことは単なる事実で、そのことにそれ以外のどんな評価も下さないけれど、「抜け道があるはずだ」といつまでも思っていることは、愚かなことだと思います。
いつもx+□の形のたし算ならいいのに!
そうなら簡単なのに!
それはそうですが、中学の数学は、そんなに簡単ではないのです。
「速さ」の文章題ならば、何でもx+□にすればいい、とはなりません。
それでも、パターンがないわけではありませんが、上のような考え方をする中学生が想像するのよりもずっと複雑なパターン把握が必要となります。
問題1や2のように、時間差で追いかけていく問題ならば、道のり=道のり の式を立てることになるでしょう。
しかし、それも、どちらの時間をxとおくかで、もう片方の時間はたし算にもひき算にもなります。
問題3のように、途中で速さを変えてある距離を進んでいく問題では、分数+分数=時間 の形の見た目の式になることが多いでしょう。
問題4のように、ある距離を互いに反対方向から進んで出会う問題は、二人の道のりの和が全体の道のりとなる式を立てるでしょう。
そういうパターンなら、あります。
でも、それは、文章を読解できるからこそのパターン把握です。
しかも、速さの3公式をマスターしていることが前提です。
問題を読まずに式を立てる方法は、ないのです。
どうか、1日も早く、目を覚まして。
いつも、そのように願って、授業をしています。
さて、まずは、こんな問題から。
1次方程式の問題です。
問題1
午前8時に、3㎞離れた学校へ兄が出かけ、兄が出発してから6分後に妹が走って同じ道を追いかけた。兄が歩く速さが分速80m、妹が走る速さが分速120mであるとき、妹が兄に追いつく時刻を求めなさい。
基本が身についている人にとっては、何とか立式できるレベルの問題です。
公立中学で使う普通の教科書にも載っている問題です。
まず、何を x とおくか。
「時刻を x とおく」とうっかり書いてしまうことがあるかもしれませんが、時刻と時間は違うのです。
、
時刻と時間。
小学校の低学年で学習している内容ですが、こういう根本の概念ほど、言葉で説明しようとするとむしろ難しいことがあります。
「今の時刻は、午後12時58分と」いうのが、時刻。
「家から学校まで30分かかる」というのが時間。
10歳未満の子どものほうが、むしろ、こうした概念を概念のまますっと理解できるのですが、そのときに学び損ねると、一生わからない・・・ということも起こります。
いくら言葉を重ねて説明しても、わからないものはわからないようなのです・・・。
それはともかく。
時刻を x とするのは、不可能ではないです。
その場合、上の問題ならば、「午前8時 x 分とする」ことになるのですが、この処理は案外厄介なので、時間を x で表したほうがスッキリすると思います。
すなわち、答案の1行目は、
「兄が x 分歩くとする」
しかし、この1行目を書き忘れる人は多いです。
あるとき、テスト直しノートを提出させる熱心な学校の先生に教わっている中学生がいました。
しかし、返却されたノートには、「?」「何で?」「どういう意味?」などの赤ペンの文字が入っていて、評価は「B」でした。
しっかり直したつもりなのに、なぜ「A」ではないのか?
テスト直しノートをどう直していいかわからない・・・。
そういう悩みを聞いて、そのテスト直しノートを見てみると、何を x とするのか書いていませんでした。
そのことに気づかず、次のテスト直しでは、もっと詳しく説明しなければいけないと思ったのか、変な方向に詳しく、文章題を線分図に表してみたり、カラフルに色ペンを使ったりしていました。
何を x とするかは必ず書きなさいと、方程式の利用の学習の間、毎回、毎回、助言したのに、何で身につかないのだろう・・・。
そして、学校の先生も、テスト直しノートに赤ペンで書き込むなら、
「何が x?」
と端的に書いたほうが伝わるのに・・・。
中学一年生は、本当に、まだ小学生の尻尾が残っている子が多く、「〇〇をxとする」といった日本語が数学の答案に必要だということが、どうしても信じられないようなのです。
だから、注意されても、すぐ忘れます。
数学は、式と答だけ書けばいいんだ、という小学生の「尻尾」が生えたままなのです。
また余談にそれてしまいました・・・。
そろそろ、問1の方程式を立てましょう。
もう一度、問題を見てください。
問題1
午前8時に、3㎞離れた学校へ兄が出かけ、兄が出発してから6分後に妹が走って同じ道を追いかけた。兄が歩く速さが分速80m、妹が走る速さが分速120mであるとき、妹が兄に追いつく時刻を求めなさい。
兄がx分歩くとする。
そうすると、妹は遅れて出発していますから、妹の時間は、(X-6)分です。
速さは問題文に書いてあるし、時間はxを使って表せます。
これは、方程式は、道のりを表すものを作ればいいですね。
追いつくまでの兄の道のりと妹の道のりは等しいです。
速さ×時間=道のり ですから、
80x=120(x-6)
これを解いて、x=18
さて、ここから時刻に直す必要があります。
兄が出発した時刻が午前8時。
そこから18分歩いたのですから、
解答は、午前8時18分です。
問題2
弟は分速73mで歩いて、家から1.7㎞離れた駅に向かって出発した。弟が出発してから15分後に姉が自転車に乗って同じ道を分速292mで弟を追いかけた。姉は弟に駅まであと何mのところで追いつくか答えなさい。
さて、方程式の文章題は、基本は求めたいものを x としますが、この問題、「駅まであと x mのところで追いつくとする」としてしまうと、式が難しくなりそうな嫌な予感がします。
方程式は、わり算の式よりも、かけ算の式を立てたほうが簡単です。
どうしてもわり算、すなわち分数の式しか立てられないこともあるけれど、今回はそうではなさそう。
そういう判断ができると、この問題は楽に解けます
これも、やはり、「姉が x 分走るとする」のほうが、速さ×時間=道のり の、簡単な式を立てられそうです。
姉が x 分走るとする。
そうすると、弟は姉よりも前に出発していますから、弟の時間は(15+x)分。
弟の道のり=姉の道のり ですから。
292x=75(15+x)
これを解いて、
x=5
姉が5分走ったことがわかりました。
では、姉の道のりは、
292×5=1460
駅までは1.7㎞=1700mですから、残りの道のりは、
1700-1460=240
答えは、240mです。
問題3
9㎞離れたところへ行くのに、はしめは時速5㎞で歩き、途中から時速3㎞で歩いたら、2時間かかった。時速5㎞で歩いた道のりを求めなさい。
よし、これは、前半の歩いた道のりを x とするので大丈夫でしょう。
方程式は、時間を表す式を立てましょう。
時速5kmで歩いた道のりを x ㎞とする。
道のりは全部で9㎞ですから、時速3㎞で歩いた道のりは、(9-x)㎞ と表すことができます。
前半の時間は、x / 5 時間。
後半の時間は、(9-x) / 3 時間。
その合計が2時間なのだから、
x / 5 +(9-x) / 3=2
これを解いて、
x=15 / 2
解答は、15 / 2㎞。
問題4
AとBが5㎞離れた場所にいる。Aは午前9時に、Bは午前9時2分に互いに向かって走り出した。Aが分速250m、Bが分速200mで走るとき、2人が出会う時刻を求めなさい。
Aが出発したのが午前9時でわかりやすいので、Aの走る時間をx分としましょう。
Bは出発が2分遅かったので、走る時間は(x-2)分となります。
今回、2人の道のりは異なります。
しかし、2人で協力して5㎞走ったのですから、2人の道のりの和が5㎞=5000mです。
Aの走る時間を x 分とする。
250x+200(x-2)=5000
これを解いて、
x=12
解答は、午前9時12分 です。
さて、ここまで逐一ヒントを出しながら、生徒と一緒に立式し、上の問題1から4まで解いたときのことです。
生徒から、言われました。
「・・・わからない」
「うん?何がわからない?」
「解いたのを見ればわかるけど、自分では式が立てられない・・・」
・・・なるほど。
「どういうところがわからない?」
ここで、長い長い沈黙がありました。
でも、何か言ってくれないと、何がどうわからないのか、私もわからないので、何か喋り出すまで、辛抱強く待ちました。
ついに、その子は口を開きました。
「・・・式の形が・・・」
「うん?」
「・・・式の形が同じじゃない」
「・・・?」
式を見直してみましょう。
問題1は、
80x=120(x-6)
問題2は、
73(15+x)=292x
問題3は、
x / 5 +(9-x) / 3=2
問題4は、
250x+200(x-2)=5000
「・・・特にどこが違うと思う?」
そう問いかけてみました。
「たすだったり、引くだったりするのが、・・・」
「たすだったり、引くだったり?どこのところが?」
「・・・x-6だったり、15+xだったり、9-xだったりするのが、わからない・・・」
「・・・」
・・・問題によって、たすだったり引くだったりするのは、当たり前じゃないの?
同じ問題じゃないんだから・・・。
心の中でそう思い、そして気づきました。
そうか。
この子は、全部たし算ならたし算、ひき算ならひき算であってほしいのか・・・。
式の形が、いつも全部同じであってほしいのか・・・。
その式の形さえ覚えれば良いという勉強がしたいのか・・・。
気持ちはわかるのです。
しかし、そういうパターン把握で方程式の文章題をこなせると夢を見ている間は、方程式の文章題は自分で解けるようにはならないのです。
文章を読んで、意味を理解して、構造を把握して、その都度関係をつかんで、式を立てる。
そういう「まっとうな解き方」が実は正解への最短距離なのですが、なぜか、それだけは絶対にしない、そんなことは許容しないという子たちがいます。
おそらく、小学生の頃から、算数の文章題を意味を読み取って式を立てることは、一切してこなかったのだと思います。
すべてパータン把握でこなしてきた。
小学校では、それでそこそこ大丈夫だった。
ときどき、「単位量あたり」とか、「割合」とか「速さ」とか、上手くいかない単元もあったけれど、そういうのは終わってしまえば、もう過去のこと。
これからも、自分はこのやり方でいく。
だって、このやり方しかわからない。
パターンがあるはずだ。
それを教えて!
ある種、背筋が寒くなるのは、こういうときです。
気持ちはわかるのですが、文章題に取り組む姿勢が、根本的に間違っているのです。
問題文を読んで、読解して、構造を把握するから、立式できるのです。
ただ、それを身につけるには、時間がかかります。
何年も何年もかかります。
だから、小学校の簡単な算数から、文章題で少しずつ練習して能力を伸ばしてきたはずなのに、小学校の頃はあまりにも簡単だったから、文章を読まずに式を立ててきた子が、今の時代、ますます増えているように感じます。
文章題にある程度対応できる子と、全く対応できない子に、はっきりと分かれます。
簡単な文章だった小学生時代に読み方を身につけなかったので、中学の数学になると、文章の構造をもう読み取れない・・・。
でも、今からでも遅くないのです。
文章を読んで、意味を理解することは、学問の基本です。
文章を読み取る必要があるのだと、本人が理解してくれれば、そこから先に進めます。
怖いのは、文章を読み取る方向に本人の気持ちが一切向かない場合です。
何かパターンがあるはずだ。
絶対あるはずだ。
そういう抜け道があるはずだ。
この先生は、それがわかっていないだけだ。
どこかに、抜け道があるんだ・・・。
いつまでもそう考えて、文章と向き合えないのです。
私は、「文章が読めない」ことは単なる事実で、そのことにそれ以外のどんな評価も下さないけれど、「抜け道があるはずだ」といつまでも思っていることは、愚かなことだと思います。
いつもx+□の形のたし算ならいいのに!
そうなら簡単なのに!
それはそうですが、中学の数学は、そんなに簡単ではないのです。
「速さ」の文章題ならば、何でもx+□にすればいい、とはなりません。
それでも、パターンがないわけではありませんが、上のような考え方をする中学生が想像するのよりもずっと複雑なパターン把握が必要となります。
問題1や2のように、時間差で追いかけていく問題ならば、道のり=道のり の式を立てることになるでしょう。
しかし、それも、どちらの時間をxとおくかで、もう片方の時間はたし算にもひき算にもなります。
問題3のように、途中で速さを変えてある距離を進んでいく問題では、分数+分数=時間 の形の見た目の式になることが多いでしょう。
問題4のように、ある距離を互いに反対方向から進んで出会う問題は、二人の道のりの和が全体の道のりとなる式を立てるでしょう。
そういうパターンなら、あります。
でも、それは、文章を読解できるからこそのパターン把握です。
しかも、速さの3公式をマスターしていることが前提です。
問題を読まずに式を立てる方法は、ないのです。
どうか、1日も早く、目を覚まして。
いつも、そのように願って、授業をしています。
2025年03月19日
学習負担の軽量化と、その効果。

画像は、都立小金井公園の大漁桜。
早咲きの桜で先週満開でした。
この時期になると、教育関係の記事が特に増えて、その中には有益なものもあるのですが、
「それはどうなんだろう?」
と思うものも、無いわけではありません。
勿論、それはどうなんだと思う私の考えもまた1つの私見であり、絶対なものではないのですが。
興味深かったのは、英単語の覚え方に関するある記事。
単語集そのままでは、
「これを1冊覚えなければならないのか」
というプレッシャーが強くなり、覚えにくいというのです。
だから、単語集の単語とその意味を、ルーズリーフに書き写す。
単語とその意味をルーズリーフに書きとると、わずか20ページ程度になる。
「何だ、これを覚えればいいんだ」
と気持ちが楽になり、覚えられる、というのです。
心理的負荷を減らすという意味で、ある種の説得力があるやり方ですし、それで効果のある人もいると思います。
覚える能力自体には問題のない人は、これで成功する可能性があります。
やる気が出なくて困っている人は、このように目先を変えてみましょう、という話だと思うのです。
しかし、挫折の可能性も目に見えています。
まず、単語集の単語をルーズリーフに書き写すというその作業に、何日かかるのだろう、という点。
単語集を書き写すことも挫折する子。
単語を書き写しただけで満足し、覚えるという作業には移行できない子。
覚えようとすると、やっぱり覚えられないので、挫折してしまう子。
そういう子のほうが多いだろうと、私は思います。
ルーズリーフに書き写すという作業時間が、全て無駄になります。
英単語を覚えられない根本の問題は、大抵の人にとって(私も含めて)、英単語が非常に覚えにくいということ。
努力しても、努力しても、記憶が消えていきます。
どうやっても、覚えにくいものは覚えにくいのです。
本をルーズリーフに変えたところで、覚えられないことは変わりません。
心理的負担を減らしたところで、能力的負担は、変わらないのです。
もの覚えが悪いということが、どれほどのことか。
頭の良い人は、それを理解していないのです。
英単語を覚えるには、その単語に触れる機会をとにかく増やす必要があります。
だから、心理的負担を乗り越えて、毎日単語集そのものを開いて、繰り返し見て、音源を聴いて、聴き込んで、自分へのテストを繰り返す人は、今よりは単語を覚えられます。
それがルーズリーフになったところで、毎日繰り返し見て、自分へのテストを繰り返す作業は必要です。
わずか20ページのルーズリーフになったところで、反復しなければ覚えられません。
「わずか20ページのルーズリーフすら覚えられない自分」と直面し、闘う覚悟が必要です。
能力不足は努力で補う。
しかし、若さのせいで、その「能力不足」に簡単に傷ついて、何もかも投げ出してしまうことは多いです。
根本にあるのは、それです。
別に、能力が足りないのは自分だけではないので、そんなくだらないことで傷ついていられない。
そう見切ることができるほどに、精神的に成長できていない生徒は多いです。
まだ10代ですから、仕方ないのですが。
やるか、やらないか。
結局、それだけです。
それを理解したうえでの「ルーズリーフ作戦」は、やってみてもいいと思います。
ただ、どうせ単語集の単語を何かに書き写すなら、フラッシュカード方式のほうが良いかもしれません。
要するに、単語帳ですね。
小さいカードの表に英単語、裏にその意味を書いて、自分にテストをしながらどんどんめくっていきます。
意味を言えた単語と言えなかった単語を別に分けて、意味を言えなかった単語へのテストを繰り返します。
カードなので、そうした整理が簡単です。
これも、勿論、カードを作っただけで満足していては、無意味。
繰り返しこのカードを使う必要があります。
反復が重要です。
これ、アプリでも、そういうことができるようになりつつあるとの話です。
正解できた単語も混ぜながら、正解できなかった単語のほうが優先的に前に出てくるように、常に順番を変えてテスト形式で出してくれるアプリ。
自分で入力するのは大変ですから、単語集を販売している教材会社が、そのアプリも提供してくれるようになると良いですね。
ゲーム形式で得点が出ると、励みになるかもしれません。
ただ、これも、結局は英単語なので、「つまらない」と言えばつまらない。
そんなのより、もっと面白いゲームをやりたい、という志向の人には向かないアプリかもしれません。
さらに、数学では、「チャート式数学」を5周やる、という方法をネットで見ました。
解くときに、時間はかけない。
問題文を読んで、10秒ないし15秒考えても解き方がわからない問題は、すぐに解答・解説を見る。
そうやって、次の問題、次の問題と解いていく。
これも、数学が苦手な人にとっては、ライトな勉強法で、「これならできる」と思う人もいそうです。
わからなかったら、すぐ答を見たらいいのですから。
しかし、これも、頭のいい人の勉強法だなあと、ある意味感心しました。
10秒なんてすぐ経ちます。
どれだけ自分の頭の回転の速さを基準にものを言っているのだろう?
せめて、1分考えたら?
1分考えて、解き方が何も浮かばない問題は、解答・解説を見る。
・・・本人の地頭が良く、ものを考える力のある場合は、効果があるかもしれない、と思います。
解き方がわからない問題はすぐに解答解説を見る。
頭の良い人は、解答解説を見ることによって、その解法が頭の中にストックされるのです。
それも、応用の効く形で。
だから、類題でその解法を利用できます。
1つの問題集を5周もすれば、いくら何でも、解法が頭の中に残るだろう・・・。
それもまた、頭の良い人の実感であり、現実とは異なります。
そもそも、1分考えてすぐに解答解説を読んでも、その咀嚼に時間がかかる人のほうが多いでしょう。
見るだけでは済まず、自分で解答解説を見ながらでも解いてみないと納得できないという人は多いので、結局時間がかかります。
しかも、時間がかかるのに、1週間後には、きれいに忘れているのです。
時間がかかるから、問題集を1周するのに、半年はかかる。
そして、1周が終わった半年後には、その大半を忘れている。
下手をすると、何も身につかないうちに、入試になってしまう・・・。
上手くいって、3周程度はできたとして。
解答解説を読んで、その解き方を暗記できたところで、応用が効かない暗記の仕方では、数値が違うだけの同じ形式の問題にしか対応できない場合も多いです。
数学が苦手というのは、そういうことです。
応用が効かないのは、蓄積がないからです。
高校数学が苦手な人の多くは、中学で学習した公式や定理を忘れています。
数ⅡBを学習する頃には、数ⅠAで学習した公式や定理を忘れています。
頭の中に残らないのです。
残そうとしても、何だかスルスルと消えていくのです。
消えていくものは消えていくのだから、仕方がないのです。
本当に数学が得意になりたいのなら、1問について、最低1時間はねばって考えてほしいのです。
たとえ1時間後、結局わからなくて解答解説を見ることになっても、1時間考える間に、脳細胞が繋がって、繋がって、頭が良くなります。
頭をよくするためには、時間をかけて考えることが必要です。
うわ滑りしがちな思考にクサビを打ち込み、地頭を良くするには、そうした苦痛を伴う作業が必要になります。
そして、頭が良くなれば、記憶力も良くなります。
そうなれば、上のような負担の軽い勉強法でも、ある程度の効果を期待できるようになるかもしれません。
向き不向きはありますから、
「やってみたい」
「やってみようかな」
と思う勉強法があったら、やってみたら良いと思います。
見た目を軽くし、負担を軽くする勉強法は、今どきの子どもたちには向いているかもしれない、とも思うのです。
たったこれだけでいいんだから、とりあえずやってみよう。
そういうことも、大切です。
ただ、本当に効果のある学習法は、基本「重い」です。
しかも、効果が表れるまで時間がかかります。
そのことは、知っていてほしいことだとも思います。
早咲きの桜で先週満開でした。
この時期になると、教育関係の記事が特に増えて、その中には有益なものもあるのですが、
「それはどうなんだろう?」
と思うものも、無いわけではありません。
勿論、それはどうなんだと思う私の考えもまた1つの私見であり、絶対なものではないのですが。
興味深かったのは、英単語の覚え方に関するある記事。
単語集そのままでは、
「これを1冊覚えなければならないのか」
というプレッシャーが強くなり、覚えにくいというのです。
だから、単語集の単語とその意味を、ルーズリーフに書き写す。
単語とその意味をルーズリーフに書きとると、わずか20ページ程度になる。
「何だ、これを覚えればいいんだ」
と気持ちが楽になり、覚えられる、というのです。
心理的負荷を減らすという意味で、ある種の説得力があるやり方ですし、それで効果のある人もいると思います。
覚える能力自体には問題のない人は、これで成功する可能性があります。
やる気が出なくて困っている人は、このように目先を変えてみましょう、という話だと思うのです。
しかし、挫折の可能性も目に見えています。
まず、単語集の単語をルーズリーフに書き写すというその作業に、何日かかるのだろう、という点。
単語集を書き写すことも挫折する子。
単語を書き写しただけで満足し、覚えるという作業には移行できない子。
覚えようとすると、やっぱり覚えられないので、挫折してしまう子。
そういう子のほうが多いだろうと、私は思います。
ルーズリーフに書き写すという作業時間が、全て無駄になります。
英単語を覚えられない根本の問題は、大抵の人にとって(私も含めて)、英単語が非常に覚えにくいということ。
努力しても、努力しても、記憶が消えていきます。
どうやっても、覚えにくいものは覚えにくいのです。
本をルーズリーフに変えたところで、覚えられないことは変わりません。
心理的負担を減らしたところで、能力的負担は、変わらないのです。
もの覚えが悪いということが、どれほどのことか。
頭の良い人は、それを理解していないのです。
英単語を覚えるには、その単語に触れる機会をとにかく増やす必要があります。
だから、心理的負担を乗り越えて、毎日単語集そのものを開いて、繰り返し見て、音源を聴いて、聴き込んで、自分へのテストを繰り返す人は、今よりは単語を覚えられます。
それがルーズリーフになったところで、毎日繰り返し見て、自分へのテストを繰り返す作業は必要です。
わずか20ページのルーズリーフになったところで、反復しなければ覚えられません。
「わずか20ページのルーズリーフすら覚えられない自分」と直面し、闘う覚悟が必要です。
能力不足は努力で補う。
しかし、若さのせいで、その「能力不足」に簡単に傷ついて、何もかも投げ出してしまうことは多いです。
根本にあるのは、それです。
別に、能力が足りないのは自分だけではないので、そんなくだらないことで傷ついていられない。
そう見切ることができるほどに、精神的に成長できていない生徒は多いです。
まだ10代ですから、仕方ないのですが。
やるか、やらないか。
結局、それだけです。
それを理解したうえでの「ルーズリーフ作戦」は、やってみてもいいと思います。
ただ、どうせ単語集の単語を何かに書き写すなら、フラッシュカード方式のほうが良いかもしれません。
要するに、単語帳ですね。
小さいカードの表に英単語、裏にその意味を書いて、自分にテストをしながらどんどんめくっていきます。
意味を言えた単語と言えなかった単語を別に分けて、意味を言えなかった単語へのテストを繰り返します。
カードなので、そうした整理が簡単です。
これも、勿論、カードを作っただけで満足していては、無意味。
繰り返しこのカードを使う必要があります。
反復が重要です。
これ、アプリでも、そういうことができるようになりつつあるとの話です。
正解できた単語も混ぜながら、正解できなかった単語のほうが優先的に前に出てくるように、常に順番を変えてテスト形式で出してくれるアプリ。
自分で入力するのは大変ですから、単語集を販売している教材会社が、そのアプリも提供してくれるようになると良いですね。
ゲーム形式で得点が出ると、励みになるかもしれません。
ただ、これも、結局は英単語なので、「つまらない」と言えばつまらない。
そんなのより、もっと面白いゲームをやりたい、という志向の人には向かないアプリかもしれません。
さらに、数学では、「チャート式数学」を5周やる、という方法をネットで見ました。
解くときに、時間はかけない。
問題文を読んで、10秒ないし15秒考えても解き方がわからない問題は、すぐに解答・解説を見る。
そうやって、次の問題、次の問題と解いていく。
これも、数学が苦手な人にとっては、ライトな勉強法で、「これならできる」と思う人もいそうです。
わからなかったら、すぐ答を見たらいいのですから。
しかし、これも、頭のいい人の勉強法だなあと、ある意味感心しました。
10秒なんてすぐ経ちます。
どれだけ自分の頭の回転の速さを基準にものを言っているのだろう?
せめて、1分考えたら?
1分考えて、解き方が何も浮かばない問題は、解答・解説を見る。
・・・本人の地頭が良く、ものを考える力のある場合は、効果があるかもしれない、と思います。
解き方がわからない問題はすぐに解答解説を見る。
頭の良い人は、解答解説を見ることによって、その解法が頭の中にストックされるのです。
それも、応用の効く形で。
だから、類題でその解法を利用できます。
1つの問題集を5周もすれば、いくら何でも、解法が頭の中に残るだろう・・・。
それもまた、頭の良い人の実感であり、現実とは異なります。
そもそも、1分考えてすぐに解答解説を読んでも、その咀嚼に時間がかかる人のほうが多いでしょう。
見るだけでは済まず、自分で解答解説を見ながらでも解いてみないと納得できないという人は多いので、結局時間がかかります。
しかも、時間がかかるのに、1週間後には、きれいに忘れているのです。
時間がかかるから、問題集を1周するのに、半年はかかる。
そして、1周が終わった半年後には、その大半を忘れている。
下手をすると、何も身につかないうちに、入試になってしまう・・・。
上手くいって、3周程度はできたとして。
解答解説を読んで、その解き方を暗記できたところで、応用が効かない暗記の仕方では、数値が違うだけの同じ形式の問題にしか対応できない場合も多いです。
数学が苦手というのは、そういうことです。
応用が効かないのは、蓄積がないからです。
高校数学が苦手な人の多くは、中学で学習した公式や定理を忘れています。
数ⅡBを学習する頃には、数ⅠAで学習した公式や定理を忘れています。
頭の中に残らないのです。
残そうとしても、何だかスルスルと消えていくのです。
消えていくものは消えていくのだから、仕方がないのです。
本当に数学が得意になりたいのなら、1問について、最低1時間はねばって考えてほしいのです。
たとえ1時間後、結局わからなくて解答解説を見ることになっても、1時間考える間に、脳細胞が繋がって、繋がって、頭が良くなります。
頭をよくするためには、時間をかけて考えることが必要です。
うわ滑りしがちな思考にクサビを打ち込み、地頭を良くするには、そうした苦痛を伴う作業が必要になります。
そして、頭が良くなれば、記憶力も良くなります。
そうなれば、上のような負担の軽い勉強法でも、ある程度の効果を期待できるようになるかもしれません。
向き不向きはありますから、
「やってみたい」
「やってみようかな」
と思う勉強法があったら、やってみたら良いと思います。
見た目を軽くし、負担を軽くする勉強法は、今どきの子どもたちには向いているかもしれない、とも思うのです。
たったこれだけでいいんだから、とりあえずやってみよう。
そういうことも、大切です。
ただ、本当に効果のある学習法は、基本「重い」です。
しかも、効果が表れるまで時間がかかります。
そのことは、知っていてほしいことだとも思います。
2025年03月13日
英語。現在完了。祖父が亡くなって5年になる。

画像は多摩湖自転車歩行者道の河津桜。
3月7日、きれいに咲いていました。
さて本題。
現在完了は、今や中2で学習する文法事項になりましたが、高校生になっても、勿論、「時制」の学習で再び登場します。
特に有名な典型題が、「祖父が死んで5年になる」という文を書き換える問題です。
まずは、過去形で単純に書くならば、それは「祖父は5年前に死んだ」ということですから、
My grandfather died five years ago.
となります。
これを、現在完了形を使って書き換える問題。
案外難しいのです。
正解からまず示しますと、
My grandfather has been dead for five years.
となります。
直訳の日本語は、
「祖父は、5年間、死んだ状態である」
ということ。
日本人の感覚では永久に出てこない表現です。
日本語からの直訳で英文を作っていこうとすると、永久に正解できないのです。
5年間は死んだ状態であるが、いずれ復活する、ということなんですかね?
英語圏の土葬文化や、復活を信じるキリスト教文化の影響なのでしょうか。
「ゾンビ」という発想も、そういうものと関係がありそうです。
火葬文化の日本には、幽霊はいても、ゾンビはいないですよね。
それはともかく、日本の子どもたちは、そういう日本の発想で、以下のような間違った英文を作ってしまいがちです。
My grandfather has been died for five years.
「死ぬのは一瞬の動作ですから、現在完了には使えないんですよ」
「・・・」
そのような文法解説は、見るのも聞くのも大嫌いな子が多く、身につかないんです。
die が動作動詞であるなら、現在完了進行形ならばいいのか?
My grandfather has been dying for five years.
これは、文法的には間違っていないですが、意味が違ってきます。
die の進行形、be dying は、「死にかけている」「瀕死の状態である」ということになります。
おじいさんは、5年間危篤状態ということになり、生きています。
というわけで、die という動詞の形容詞形 dead は、必ず覚えなければならないのですが、それとあわせて、形容詞は、be 動詞とともに用いるという文法知識もなかなか身につかないので、
My grandfather has dead for five years.
という間違った英文を作ってしまう子もいます。
こういうミスが多いのです。
この典型題は、陳腐な典型題であるにも関わらず、いまだに攻略できない子が多いので、定期テストや大学入試に出題され続けるのです。
このブログに繰り返し書いてきたことですが、「難しいことを簡単にしたい」という欲望の強い子たちがいます。
勉強なんて、そんなに難しくないはずだ。
自分は、小学生の頃は、勉強ができた。
だから、もっと簡単になるはずだ。
簡単な教え方ができない先生が無能なのだ。
いや。
そこまで考えている子はさすがに少ないと思いますが、難しいことを、自分のやり方で簡単に「まるっとまるめ」ようとする子は、存在します。
そして、結局、間違い続けます。
複雑なことは、もともと複雑なので、複雑なまま理解するしかない場合があります。
この程度の難しさは、高校英語ならばもう仕方のない複雑さです。
そのように理解して受け止めれば、頭にスッとなじみやすくなる人も案外多いのではないかと思うのです。
というわけで、
My grandfather died five years ago.
=My grandfather has been dead for five years.
これは、しっかり覚えられたとして。
しかし、それだけで終わらないのが、この典型題の複雑さです。
他にも、あと3通り、この書き換えがあるのです。
まず、時を表す主語 it を用いた書き換えから。
It is five years since my grandfather died.
「祖父が亡くなってから、5年だ」
という文です。
上の文は、動詞が is で現在形ですが、これは、現在完了形で述べることもできます。
It has been five years since my grandfather died.
いずれにしても、since 節は、過去形です。
このあたりも混乱する人がいますので、要注意です。
since の後ろは、その状態・動作が始まった起点を表すので、それは過去のことですから、過去形で語ります。
さらに、書き換えは、もう1つあります。
Five years have passed since my grandfather died.
「祖父が死んでから、5年が過ぎた」
という文です。
five years は複数なので、has ではなく have になることも注意が必要です。
まとめますと、「祖父が死んで5年になる」には、5通りの表現があります。
My grandfather died five years ago.
My grandfather has been dead for five years.
It is five years since my grandfather died.
It has been five years since my grandfather died.
Five years have passed since my grandfather died.
さて、練習問題を解いてみましょう。
次の英文をほぼ同じ意味になるように書き換えた場合、( )に適語を補充せよ。
(1) We have been friends for five years.
=( )( )( ) passed since we ( ) friends.
上の5通りの文は理解したつもりでいるのに、こういう問題になると、応用がきかない・・・。
そういう悩みを抱えている人もいるかもしれません。
5通りの書き換えのうちのどれなのか、判断がつかない、というのです。
上の問題で言えば、2行目の passed が、ヒントです。
この単語を使うのは、主語が年数の場合のときです。
だから、
=(Five)(years)( ) passed since we ( ) friends.
までは、OK。
ただ、その後が案外埋まらない、という人もいます。
何か、この( )、無くても良くない?と思ってしまうようです。
3個目の ( ) は、何なのか?
時制は、現在完了だった、ということを思い出せば、大丈夫。
=(Five)(years)(have) passed since we ( ) friends.
です。
さて、最後の ( ) には、何を入れるのか?
ここで、we are friends とか、we were friends としてしまうミスも多いです。
since 節は、動作の起点です。
「友達である」ではなく、「友達になる」という表現が適切です。
したがって、正解は、
=(Five)(years)(have) passed since we (became) friends.
となります。
(2) It has been three years since she moved to this town.
=She ( )( )( ) this town ( ) three years.
さて、これも難しいですね。
よくある誤答が、
=She (has)(moved)(to) this town (since) three years.
というもの。
これは、よく意味を考えて、書き換える必要あります。
3年間も引っ越しを続けているのは、おかしいです。
彼女は3年間、この町に住んでいるはずです。
だから、正解は、
=She (has)(lived)(in) this town (for) three years.
です。
・・・もうわかんないから、諦める・・・。
どうか、そんなふうに、投げ出さないでください。
書き換えというと、元の文に出てくる単語と同じ単語しか使わないと思い込んでいる人がいますが、そんなことはありません。
「元の文と同じ単語じゃないのなら、わかるわけないじゃん!」とは思わないで。
わかるんです。
正解している人もいるんですから。
頭の表面のところで何か適当にくるくるっと処理して問題を解いていれば全部正解だった小学生の頃の成功体験は、もう忘れてください。
勉強は、もう少し深く考えるものです。
年齢とともに脳は発達しているのですから、より深く、複雑なことを学習できるのです。
英語は、知識の積み上げ、蓄積が影響します。
中学英語はさぼってきた。
あるいは、定期テストが終われば、全部忘れてきた。
でも、高校生になったから、今度は英語も頑張ろうと思ったのに、何だ、もうダメなんだ・・・。
そんなふうに、諦めないでください。
中学英語が身についていないことは、確かに大変なハンデですが、それは自分が招いたことなので、背負う覚悟を持ってください。
身についていなかったことは、1つ1つ、今から身につければ、間に合います。
英語が得意な人たちは、毎日英語を勉強してきたのです。
定期テストが終わっても、記憶を捨てず、反復してきたのです。
その努力が無効になるわけがないのです。
彼らは、はるか先にいます。
でも、今から努力すれば、その努力も、無効ではないのです。
ここから、頑張る。
そういう気持ちで、繰り返し練習してください。
3月7日、きれいに咲いていました。
さて本題。
現在完了は、今や中2で学習する文法事項になりましたが、高校生になっても、勿論、「時制」の学習で再び登場します。
特に有名な典型題が、「祖父が死んで5年になる」という文を書き換える問題です。
まずは、過去形で単純に書くならば、それは「祖父は5年前に死んだ」ということですから、
My grandfather died five years ago.
となります。
これを、現在完了形を使って書き換える問題。
案外難しいのです。
正解からまず示しますと、
My grandfather has been dead for five years.
となります。
直訳の日本語は、
「祖父は、5年間、死んだ状態である」
ということ。
日本人の感覚では永久に出てこない表現です。
日本語からの直訳で英文を作っていこうとすると、永久に正解できないのです。
5年間は死んだ状態であるが、いずれ復活する、ということなんですかね?
英語圏の土葬文化や、復活を信じるキリスト教文化の影響なのでしょうか。
「ゾンビ」という発想も、そういうものと関係がありそうです。
火葬文化の日本には、幽霊はいても、ゾンビはいないですよね。
それはともかく、日本の子どもたちは、そういう日本の発想で、以下のような間違った英文を作ってしまいがちです。
My grandfather has been died for five years.
「死ぬのは一瞬の動作ですから、現在完了には使えないんですよ」
「・・・」
そのような文法解説は、見るのも聞くのも大嫌いな子が多く、身につかないんです。
die が動作動詞であるなら、現在完了進行形ならばいいのか?
My grandfather has been dying for five years.
これは、文法的には間違っていないですが、意味が違ってきます。
die の進行形、be dying は、「死にかけている」「瀕死の状態である」ということになります。
おじいさんは、5年間危篤状態ということになり、生きています。
というわけで、die という動詞の形容詞形 dead は、必ず覚えなければならないのですが、それとあわせて、形容詞は、be 動詞とともに用いるという文法知識もなかなか身につかないので、
My grandfather has dead for five years.
という間違った英文を作ってしまう子もいます。
こういうミスが多いのです。
この典型題は、陳腐な典型題であるにも関わらず、いまだに攻略できない子が多いので、定期テストや大学入試に出題され続けるのです。
このブログに繰り返し書いてきたことですが、「難しいことを簡単にしたい」という欲望の強い子たちがいます。
勉強なんて、そんなに難しくないはずだ。
自分は、小学生の頃は、勉強ができた。
だから、もっと簡単になるはずだ。
簡単な教え方ができない先生が無能なのだ。
いや。
そこまで考えている子はさすがに少ないと思いますが、難しいことを、自分のやり方で簡単に「まるっとまるめ」ようとする子は、存在します。
そして、結局、間違い続けます。
複雑なことは、もともと複雑なので、複雑なまま理解するしかない場合があります。
この程度の難しさは、高校英語ならばもう仕方のない複雑さです。
そのように理解して受け止めれば、頭にスッとなじみやすくなる人も案外多いのではないかと思うのです。
というわけで、
My grandfather died five years ago.
=My grandfather has been dead for five years.
これは、しっかり覚えられたとして。
しかし、それだけで終わらないのが、この典型題の複雑さです。
他にも、あと3通り、この書き換えがあるのです。
まず、時を表す主語 it を用いた書き換えから。
It is five years since my grandfather died.
「祖父が亡くなってから、5年だ」
という文です。
上の文は、動詞が is で現在形ですが、これは、現在完了形で述べることもできます。
It has been five years since my grandfather died.
いずれにしても、since 節は、過去形です。
このあたりも混乱する人がいますので、要注意です。
since の後ろは、その状態・動作が始まった起点を表すので、それは過去のことですから、過去形で語ります。
さらに、書き換えは、もう1つあります。
Five years have passed since my grandfather died.
「祖父が死んでから、5年が過ぎた」
という文です。
five years は複数なので、has ではなく have になることも注意が必要です。
まとめますと、「祖父が死んで5年になる」には、5通りの表現があります。
My grandfather died five years ago.
My grandfather has been dead for five years.
It is five years since my grandfather died.
It has been five years since my grandfather died.
Five years have passed since my grandfather died.
さて、練習問題を解いてみましょう。
次の英文をほぼ同じ意味になるように書き換えた場合、( )に適語を補充せよ。
(1) We have been friends for five years.
=( )( )( ) passed since we ( ) friends.
上の5通りの文は理解したつもりでいるのに、こういう問題になると、応用がきかない・・・。
そういう悩みを抱えている人もいるかもしれません。
5通りの書き換えのうちのどれなのか、判断がつかない、というのです。
上の問題で言えば、2行目の passed が、ヒントです。
この単語を使うのは、主語が年数の場合のときです。
だから、
=(Five)(years)( ) passed since we ( ) friends.
までは、OK。
ただ、その後が案外埋まらない、という人もいます。
何か、この( )、無くても良くない?と思ってしまうようです。
3個目の ( ) は、何なのか?
時制は、現在完了だった、ということを思い出せば、大丈夫。
=(Five)(years)(have) passed since we ( ) friends.
です。
さて、最後の ( ) には、何を入れるのか?
ここで、we are friends とか、we were friends としてしまうミスも多いです。
since 節は、動作の起点です。
「友達である」ではなく、「友達になる」という表現が適切です。
したがって、正解は、
=(Five)(years)(have) passed since we (became) friends.
となります。
(2) It has been three years since she moved to this town.
=She ( )( )( ) this town ( ) three years.
さて、これも難しいですね。
よくある誤答が、
=She (has)(moved)(to) this town (since) three years.
というもの。
これは、よく意味を考えて、書き換える必要あります。
3年間も引っ越しを続けているのは、おかしいです。
彼女は3年間、この町に住んでいるはずです。
だから、正解は、
=She (has)(lived)(in) this town (for) three years.
です。
・・・もうわかんないから、諦める・・・。
どうか、そんなふうに、投げ出さないでください。
書き換えというと、元の文に出てくる単語と同じ単語しか使わないと思い込んでいる人がいますが、そんなことはありません。
「元の文と同じ単語じゃないのなら、わかるわけないじゃん!」とは思わないで。
わかるんです。
正解している人もいるんですから。
頭の表面のところで何か適当にくるくるっと処理して問題を解いていれば全部正解だった小学生の頃の成功体験は、もう忘れてください。
勉強は、もう少し深く考えるものです。
年齢とともに脳は発達しているのですから、より深く、複雑なことを学習できるのです。
英語は、知識の積み上げ、蓄積が影響します。
中学英語はさぼってきた。
あるいは、定期テストが終われば、全部忘れてきた。
でも、高校生になったから、今度は英語も頑張ろうと思ったのに、何だ、もうダメなんだ・・・。
そんなふうに、諦めないでください。
中学英語が身についていないことは、確かに大変なハンデですが、それは自分が招いたことなので、背負う覚悟を持ってください。
身についていなかったことは、1つ1つ、今から身につければ、間に合います。
英語が得意な人たちは、毎日英語を勉強してきたのです。
定期テストが終わっても、記憶を捨てず、反復してきたのです。
その努力が無効になるわけがないのです。
彼らは、はるか先にいます。
でも、今から努力すれば、その努力も、無効ではないのです。
ここから、頑張る。
そういう気持ちで、繰り返し練習してください。
2025年03月08日
生徒を募集しています。2025年3月。

生徒を募集しています。
現在の成績は問いません。
未来の秀才を求めています。
小さな個別指導塾ですが、1人1人の成績を確実に上げることを目標に、実績を上げています。
担当は、受験指導30年のベテラン。
受け持った生徒の成績を本当に上げることが目的の「学習トレーナー」です。
必要な時期に必要な学習内容を提示します。
高校受験は、毎年全員が第一志望校に合格しています。
大学受験も、毎年、大きな成果を出しています。
詳しくは、合格発表のページをご覧ください。
◎時間
1回の授業は90分です。
月曜日から土曜日までの各曜日
16:40~18:10 , 18:20~19:50 , 20:00~21:30
◎現在空いている時間帯
2025年3月現在
木曜日16:40~18:10
金曜日18:20~19:50
◎授業形態
1対1の完全個別指導です。
通塾できない遠距離の方のリモート授業も承っております。
体調不良や悪天候の場合のリモート授業も随時承っております。
◎指導科目
受験算数・国語
小学校一般算数
中学各学年の数学・英語
中高一貫校 数学・英語
高校受験 5科
(理・社は都立受験の中3限定で、90分で2科目も可能です)
高校生各学年の数学・英語
大学受験 数学
大学受験 英語
大学受験 国語
内部進学・推薦入試向けの内申重視の数学・英語も承ります。
英検など各種英語検定対策も行っております。
◎費用
週1回 受講で、月額22,000円
週2回 受講で、月額38,000円
(内訳 90分1コマ4,500円、月5コマ以上受講される場合は、5コマ目以降は1コマ4,000円。諸経費・教材費月額4,000円。)
他に入会金を10,000円いただきます。
◎所在地
三鷹市下連雀3-33-13 三鷹第二ビル305
三鷹駅南口から徒歩5分。赤鳥居通りにある、春の湯の斜め前のビルです。1階がセブンイレブンです。
◎入会までの流れ
まず、無料体験授業をお受けください。
左の「お問い合わせ」ボタンを押し、必要事項をご記入のうえ、送信してください。
スマートフォンでご覧の方は、画面を一番下までスクロールし、「パソコン画面に切り替える」を押しますと、パソコン画面が表示されます。
緑色の「お問い合わせ」ボタンを押してください。
返信に数日かかることがあります。ご了承ください。
基本は授業中のため、電話でのお問い合わせはご遠慮いただけますと幸いです。
以下の内容をご記入いただけますと、以後のやりとりがスムーズです。
①お子様の学校名
②学年
③性別
④ご希望の通塾曜日・時間帯
⑤ご希望の体験授業日時
⑥希望科目
⑦体験授業の希望内容(例 「1次関数」 など)
受験生の健康に留意し、講師との距離は2メートルを保ち、毎時間、換気と机・椅子の消毒を行っております。
現在、またコロナが流行っております。
授業時は、受講生全員に手洗いとマスクの着用をお願いしております。
お問い合わせ、お待ちしております。
2025年03月07日
学年末テストの後の学習内容は重要です。

まだ中学生ですと、情報の価値があまり理解できていない子は多いです。
情報を正確に把握すること、私に正確に伝達することに関して、意識が低いのです。
これは、学力とは関係なく、むしろその子の性格と関係があることなのだと思います。
今回の学年末テストでは。
「テストの時間割、発表になりましたか?数学は何日ですか?」
「・・・2月24日」
「・・・2月24日の月曜日ですか?2月24日は、天皇誕生日の振替休日で学校は休みですが」
「・・・!」
日程表を確認せずに、うろ覚えで答えているのです。
「授業の振替が必要か必要でないのか、必要ならば何日の何時からにするのかを決めるために、テスト時間割は重要なのですが」
「・・・必要ないです」
「・・・今、面倒だから切り捨てましたね。必要ないわけないんですよ。テスト期間中、翌日のテスト科目に数学がない日に、数学の授業を受けることになるかもしれないんですよ」
当日にならないと、そのことの重要性がわからないのだろうと思います。
色々なことで頭がいっぱいで、今日・明日のことしか考えられない。
そういう気持ちは、わからないでもないのですが、これは、想像力が足りないこととも関係があるのでしょう。
振替の決定が遅く、直前になって、何日の何時からの授業に振替えられませんか、と問い合わせてくるのですが、直前では、もう授業は埋まっている場合が多いのです。
いつ来ても、自分1人しかいない教室。
生徒は自分1人。
自分が授業を受けている時間以外は、全部空いている。
そんな錯覚をしているのではないか?
そう思うことすらあります。
早めに互いに振り替えるから、空きコマに移動できるので、ご協力いただきたいところです。
テスト範囲を私に正確に伝達できない子も相変わらずいます。
中学の数学ならば、教科書準拠ワークを私も持っていますので、テスト範囲が教科書の何ページから何ページなのかを言ってくれれば、正確に把握できます。
しかし、高校数学の場合は、学校ごとに教科書が異なるので、さすがに用意できません。
教科書のページ数だけではわからないので、教科書そのものを持ってきてと頼んでも、忘れてくる高校生は多いです。
テスト範囲の情報は、教科書と問題集のページ数だけ。
これではわからないと告げると、初めてそのことに気づいて、大体のテスト範囲を伝えてきますが、正確かどうかは、わかりません。
これまで40点しか取れなかった子に、60点を取ってもらうためのテスト対策ならば、テスト範囲の数ページの誤差など、どうとでもなります。
しかし、80点を取れるようになった子に、90点を取ってもらうテスト対策をする場合、数ページの誤差は致命傷です。
テスト範囲を自分が完全に暗記できているとなぜ思うのだろう?
その過信はどこから来るのだろう?
そんなふうに思うこともあります。
いや、それは過信ではなく、私に正確なテスト日程やテスト範囲を伝達することの重要性が理解できていないのでしょう。
自分の不利益につながる可能性が、わかっていないのだと思います。
この子がそのまま社会に出たら、書類やデータを正確に確認しないで、うろ覚えの適当な報告を上司にして、その態度を不審に感じた上司に怒られて、しかし本人はパワハラだと感じ、怖くなって会社に行けなくなって・・・と、極端なことを想像してしまうこともあります。
もっとも、今どきの会社の上司は、そうなることを予測して、優しく優しく、書類やデータを正確に確認しながら報告するのだよーと教えてくれるのかもしれません。
必要なことが学生の間に身につかないので、社会に出てから教育しなければならない。
大変、申し訳ありません。
こちらもできる限り頑張っているのですが。
情報の価値、情報は正確でなければならないことは、早めに理解してほしいことです。
あるいは、本人にはもうどうにもならないなら、保護者が介入しないと、色々とまずいことが起こります。
例えば、大学受験の場合。
今は、色々な形の受験があります。
学校推薦。
総合型選抜。
公募推薦。
一般入試でも、共通テスト利用だの、外部試験利用だの、全学部一斉だの、学部別だの・・・。
保護者としては、自分の頃の大学入試とあまりにも違うので、ギブアップしたくなり、本人に任せたくなるかもしれません。
しかし、保護者に理解できないことを、本人が理解できるはずがないのです。
どの大学のどの学部に、どの科目が必要なのか。
そんなことすら、間違えてしまう子もいます。
学部入試の国語に漢文が出題されることを、受験3か月前まで知らなかった高三の生徒もいました。
血の気が引くような、そんなことも、本人に任せていると起こります。
そんな先のことではなく、身近なことでいえば。
学年末テストが終わって、春休みに入ると、言われてもいないのに一念発起して部屋の大掃除を始め、前学年の教科書や教材を全部捨ててしまう子がたまにいます。
しかし、公立中学生は、それは絶対にやってはいけないことです。
なぜなら、次の学年の1学期の中間テストの範囲は、今回の学年末テストの範囲の続きからとなる可能性があるからです。
学年末テストが終わって、この3月に学習している内容は、次の学年の1学期中間テストの範囲に含まれる可能性があるのです。
勿論、そうではない可能性もあります。
4月に先生が変わった場合などは特に、もう面倒くさいから、「前年度の復習」というざっくりしたテスト範囲は示すものの、厳密に学年末テストの範囲の直後から、とはならないかもしれません。
しかし、なる可能性もあります。
この4月から、中学校は教科書が変わります。
前年度の教材など、書店を探しても、もう存在しません。
今ある教材を捨ててはいけません。
特に英語と国語は、教科書と準拠ワークを捨てたら、致命傷になります。
数学もそうです。
中1の最後の単元「データの分析と活用」を、今まさに学習し始めたタイミングの中1は多いと思います。
何か数学っぽくないから、どうでもいい単元っぽい・・・。
いえいえ。
これは、高校数Ⅰでまたがっつり学習することになり、数Bでも、その発展的内容をがっつり学習し、大学入試共通テストでも、必ず出題される単元です。
捨てるわけにいかない重要単元です。
中2の最後の単元「確率」もそうです。
これは、高校数Aでさらに発展的に学習することになる重要単元です。
中学で基本を理解しておかないと、苦労します。
そのように重要度の高い単元ですから、翌年度の1学期中間テストの範囲に組み込まれる可能性は高いのです。
高校受験の受験勉強をする場合も、教科書は、詳しく丁寧で一番わかりやすい教材です。
中学生のうちは、教科書・教材は捨てないでおきましょう。
高校に合格した後で、一気に資源ゴミに出しましょう。
と、最後に、重要な情報を残して、今回は、これまで。
2025年03月01日
2025年02月26日
受験算数。直方体の展開図に関する、ちょっとした難問。

上の図は、直方体の展開図です。
(1) 図のアの長さを求めなさい。
(2) 上の図の直方体の体積を求めなさい。
自分で解いてみたい方は、ここでいったんブログを閉じてください。
この問題、わかってみれば簡単なのですが、頭が固いと、意外と苦戦します。
まず、図の見た目が、普段見慣れている直方体と異なることが、わかりにくくなる一因でしょう。
このT字形が直方体の展開図であることがそもそも理解できない、ということがあり得ます。
手を使って、図に書き込んでみる習慣のない子も苦戦します。
ただ図を眺めるだけで終わってしまうのです。
「何か書き込んでみて」
と問いかけても、
「書き方がわからない」
と答えます。
すべてが杓子定規で、解き方を教わったことのある問題しか解けない・・・。
図に何か書き込むのなら、その書き方も教わらないとわからない・・・。
臨機応変に対処するということができないのです。
「展開図は、普通、折れ線の点線が入っていますよね。それを書き込んでみましょう」
そのように問いかけても、書いていない折れ線は復元できないと言いたげに、私を見つめ返す・・・。
日頃の観察力が不足しているので、折れ線はどんなふうに入っていたのか、思い出すことができないのかもしれません。
直方体なのだから、もともとある線分と平行か垂直の点線が描かれるはず・・・という知識がない。
そういうこともあるかもしれません。
シンプルに見えて、子どもの学力を測るのに適切な問題。
この問題は良問です。
さて、解答編です。
この図のわかりにくさは、いつもの直方体の展開図とは向きが異なっていることにあります。
いつもなら、2つの底面は上下に描かれているものですが、これは、左右に2つの底面が飛び出ています。
そのことに気づけば、後の発想はかなり楽になると思います。
必要な折れ線を図に書き込んでみましょう。

これでかなりわかりやすくなりました。
展開図を組み立てたとき、4㎝の辺は、上の図の位置になります。
4㎝の長さとなる辺も赤で書き込みました。
また、アの辺と同じ長さの辺、2か所も、赤で書き込みました。
これでわかりました。
(1)は、
8-4=4
4÷2=2
で、アは、2㎝です。
続いて(2)
直方体の体積。
(1)で、直方体の底面の縦は2㎝、横は4㎝とわかりました。
では、直方体の高さは?
これも、もう簡単です。
10㎝のうち、2か所の2㎝を取り除けば、高さが求められます。
10-2×2=6
高さは6㎝とわかりました。
したがって、直方体の体積は、
2×4×6=48
答えは、48立方㎝
わかってしまえば簡単なのです。
でも、行き詰ってしまう子も多い。
わかるまで、自力で格闘してみたい問題です。
2025年02月23日
2025年度入試結果です。

今年度の入試結果が出そろいました。
結果は以下の通りです。
2025年度入試結果。
◎中学受験の部
受験生在籍者なし。
◎高校受験の部
受験生在籍者なし。
◎大学受験の部
麻布大学獣医学部 合格
専修大学文学部 合格
国士舘大学文学部 合格
なお、前年度までの入試合格結果は以下の通りです。
◎大学受験の部
2024年度
星薬科大学薬学部
横浜薬科大学薬学部
帝京平成大学薬学部
日本薬科大学薬学部
明治大学法学部
法政大学法学部
成蹊大学法学部
明治大学政治経済学部
中央大学経済学部
成蹊大学経済学部
東洋大学経済学部
東洋大学経営学部
2023年度 受験生在籍者なし
2022年度 明治大学政治経済学部
2021年度 東京外国語大学言語文化学部
2020年度 東京電機大学工学部
2019年度 東京外国語大学言語文化学部
2018年度
早稲田大学政治経済学部
中央大学経済学部
成蹊大学経済学部
東洋大学経済学部
デジタルハリウッド大学(推薦入試)
2017年 受験生在籍者なし
2016年度 埼玉大学教育学部
中央大学文学部
◎高校受験の部
2024年度 都立調布北高校
2023年度 都立松ケ谷高校
2022年度 都立蘆花高校
2021年度 都立神代高校
2020年度 都立調布北高校
2019年度 都立新宿高校
2018年度
都立西高校
都立南平高校
女子美術大学付属高校
2017年度・2016年度
受験生在籍者なし
2015年度
都立神代高校
都立調布南高校
2014年度
都立青山高校
都立豊多摩高校
都立杉並高校
◎中学受験の部
2024年度 八女学院
2023年度 受験生在籍者なし
2022年度 明治学院中学校
2020年度 東京電機大学中学校
2018年度 恵泉女学院
息つく間もなく、新年度の受験指導が始まっています。
新入生を募集しています。
現在の成績は、問いません。
未来の秀才を求めています。
小さな個別指導塾ですが、1人1人の成績を確実に上げることを目標に、実績を上げています。
担当は、受験指導30年のベテラン。
「上手な授業」を行うパフォーマーもいいですが、受け持った生徒の成績を本当に上げることが目的の「学習トレーナー」です。
必要な時期に必要な学習内容を提示します。
大学受験英語は、受験科目の中でも最大の得点源として、筆記・リスニングで高得点を取るための授業を行っています。
英語は常に得意科目でありたい。
他の科目の少しの失敗は楽にカバーできる英語得点力を実現しています。
大学受験数学は、得意な人は得点源としてのびのびと能力を伸ばし、また、苦手な人は、他の科目に迷惑をかけない得点を必ず確保することを目標に、入試の出題傾向にあわせた、演習中心の実戦的な授業を行っています。
数学は苦手だが大学受験にどうしても必要な人、歓迎します。
高校入試においては、数学・英語は勿論、5教科すべての指導を行っています。
こちらも入試問題の出題傾向に焦点を絞り、必要な知識を身につけた上での実戦的な入試対策を行っています。
都立入試の数学・英語は得点源。
さらに、他の各科目も、得意科目なら90点以上を。
苦手科目でも、80点を。
そうした形で入試の朝を迎えることを毎年の目標とし、成果を上げています。
また、私立入試・都立自校作成校入試は、英語・数学ともに学校で学ぶ内容だけでは不足があります。
早くから志望を定めている方には、定期テスト対策で内申を確保しつつ、学校のカリキュラムを離れて入試に向けた発展的な学習を計画的に指導しています。
中学受験は、受験算数をメインとした指導を行っています。
他科目の受講もご相談に応じます。
当塾だけで入試対策をする方も、他の塾の補習の形で活用される方も歓迎です。
受験生が卒業し、現在、授業コマに空きがあります。
新規の生徒を募集しています。
塾は3月が新学期。
春は塾選びの時期です。
パソコン画面に変更の上、緑色のお問合わせボタンから、ご連絡ください。
まずは無料体験授業を受けてください。
ご連絡、お待ちしております。
結果は以下の通りです。
2025年度入試結果。
◎中学受験の部
受験生在籍者なし。
◎高校受験の部
受験生在籍者なし。
◎大学受験の部
麻布大学獣医学部 合格
専修大学文学部 合格
国士舘大学文学部 合格
なお、前年度までの入試合格結果は以下の通りです。
◎大学受験の部
2024年度
星薬科大学薬学部
横浜薬科大学薬学部
帝京平成大学薬学部
日本薬科大学薬学部
明治大学法学部
法政大学法学部
成蹊大学法学部
明治大学政治経済学部
中央大学経済学部
成蹊大学経済学部
東洋大学経済学部
東洋大学経営学部
2023年度 受験生在籍者なし
2022年度 明治大学政治経済学部
2021年度 東京外国語大学言語文化学部
2020年度 東京電機大学工学部
2019年度 東京外国語大学言語文化学部
2018年度
早稲田大学政治経済学部
中央大学経済学部
成蹊大学経済学部
東洋大学経済学部
デジタルハリウッド大学(推薦入試)
2017年 受験生在籍者なし
2016年度 埼玉大学教育学部
中央大学文学部
◎高校受験の部
2024年度 都立調布北高校
2023年度 都立松ケ谷高校
2022年度 都立蘆花高校
2021年度 都立神代高校
2020年度 都立調布北高校
2019年度 都立新宿高校
2018年度
都立西高校
都立南平高校
女子美術大学付属高校
2017年度・2016年度
受験生在籍者なし
2015年度
都立神代高校
都立調布南高校
2014年度
都立青山高校
都立豊多摩高校
都立杉並高校
◎中学受験の部
2024年度 八女学院
2023年度 受験生在籍者なし
2022年度 明治学院中学校
2020年度 東京電機大学中学校
2018年度 恵泉女学院
息つく間もなく、新年度の受験指導が始まっています。
新入生を募集しています。
現在の成績は、問いません。
未来の秀才を求めています。
小さな個別指導塾ですが、1人1人の成績を確実に上げることを目標に、実績を上げています。
担当は、受験指導30年のベテラン。
「上手な授業」を行うパフォーマーもいいですが、受け持った生徒の成績を本当に上げることが目的の「学習トレーナー」です。
必要な時期に必要な学習内容を提示します。
大学受験英語は、受験科目の中でも最大の得点源として、筆記・リスニングで高得点を取るための授業を行っています。
英語は常に得意科目でありたい。
他の科目の少しの失敗は楽にカバーできる英語得点力を実現しています。
大学受験数学は、得意な人は得点源としてのびのびと能力を伸ばし、また、苦手な人は、他の科目に迷惑をかけない得点を必ず確保することを目標に、入試の出題傾向にあわせた、演習中心の実戦的な授業を行っています。
数学は苦手だが大学受験にどうしても必要な人、歓迎します。
高校入試においては、数学・英語は勿論、5教科すべての指導を行っています。
こちらも入試問題の出題傾向に焦点を絞り、必要な知識を身につけた上での実戦的な入試対策を行っています。
都立入試の数学・英語は得点源。
さらに、他の各科目も、得意科目なら90点以上を。
苦手科目でも、80点を。
そうした形で入試の朝を迎えることを毎年の目標とし、成果を上げています。
また、私立入試・都立自校作成校入試は、英語・数学ともに学校で学ぶ内容だけでは不足があります。
早くから志望を定めている方には、定期テスト対策で内申を確保しつつ、学校のカリキュラムを離れて入試に向けた発展的な学習を計画的に指導しています。
中学受験は、受験算数をメインとした指導を行っています。
他科目の受講もご相談に応じます。
当塾だけで入試対策をする方も、他の塾の補習の形で活用される方も歓迎です。
受験生が卒業し、現在、授業コマに空きがあります。
新規の生徒を募集しています。
塾は3月が新学期。
春は塾選びの時期です。
パソコン画面に変更の上、緑色のお問合わせボタンから、ご連絡ください。
まずは無料体験授業を受けてください。
ご連絡、お待ちしております。
2025年02月18日
英語。英検二次面接が上手くいかない。

今年も野川公園にセツブンソウが咲きました。
さて、英検などの二次面接、すなわちスピーキングテストになると、力を発揮できない人たちがいます。
それでも、英検準2級までなら、1週間程度の調整で何とか合格できる場合が多いですが、2級以上になると、スピーキングテストの内容も多少複雑になります。
一方、英語の四技能、すなわち「読む」「書く」「聴く」「話す」の中で、「話す」は、本人がほとんど練習しないで済ませてきていることがあり、そんなに短期間で簡単に能力の伸びる分野でもないため、苦戦することになります。
教科書の音読すら、勧められても、やらない。
英語を目の前で読むように言われたときだけ、しぶしぶ読む。
それなのに、英検に合格することは、普通に期待している・・・。
いや、それは矛盾していますよ。
英語を口に出すことができないと、スピーキングテストで良い点は取れないです。
例えば、英検2級のこんな過去問。
3コマのマンガの内容を英語で説明する問題です。
マンガは示せないので、代わりに模範解答を示します。
① One day, Ken started a teacher training program at a kindergarten.
ある日、ケンは幼稚園で教師トレーニングプログラムを受け始めました。
A woman said to him, "You'll be taking care of three children today."
女性は彼に言いました。「あなたは今日、3人の子どもたちの世話をします」
② Later that day, the children were playing with rabbits.
その日のその後、子どもたちはウサギと遊んでいました。
Ken was fixing a fence.
ケンは柵を修理していました。
③ Thirty minutes later, the children were washing their hands.
30分後、子どもたちは手を洗っていました。
Ken was thinking of reading a book to them.
ケンは彼らに本を読むことを考えていました。
それぞれのコマの冒頭や、実際のセリフは、マンガの中に描かれていますので、かなり補助があります。
あとは、マンガの通りに描写すればいいのです。
まず1コマ目。
冒頭の1文は、問題に指定されていますので、それをそのまま読むだけです。
その次の第2文で、早くも文法ミスをしてしまう人がいます。
「・・・The teacher told him that ・・・」
「うん・・・。動詞の tell を使うと、that を用いることになり、間接話法で語らなくてはならないです。that 節は難しいですよ」
「・・・The teacher said that ・・・」
「うん。それも、同じです。that と言ってしまうと、that 節になるので、主語や時制を考えなくてはならなくて、難しいですよ」
「・・・The teacher telled that ・・・」
「・・・」
途中で止められたので、動揺して、助言がよく耳に入らなくなってしまうのです。
初回の練習で、この件をしっかり助言したら、以後は間違えないのならいいのですが、毎回、このミスが口をついて出てしまう人もいます。
英語を話さなければならないということで頭が一杯なうえ、文法があまり好きではないので、that 節を使うと間接話法で語らねばならなくなることを毎回忘れてしまうのです。
マンガ中のセリフをそのまま使いたいときは、直接話法です。
A woman said to him, "You'll be taking care of three children today."
このほうが楽です。
これを、that 節を用いて間接話法で語るならば、
A woman told him that he would be taking care of three children that day.
と、that 節の主語や時制を変えなければならず、その場でスピーキングするにはレベルが上がります。
それができれば凄いですし、英検準1級の模範解答は、間接話法のことも多いです。
しかし、ミスをしてしまう可能性が高いですから、ここは、直接話法で逃げたい。
それなのに、そっちにいったらダメだよという方向に必ず向かっていってしまうのが、スピーキングが苦手な子の宿命。
本番も、that 節を使ってしまうかもしれません。
その分の減点はあらかじめ見込んで、他でカバーできれば合格できますから、まあ、仕方ない。
むしろ、問題は、その先にあります。
2コマ目の模範解答は。
② Later that day, the children were playing with rabbits.
その日の後、子どもたちはウサギと遊んでいました。
Ken was fixing a fence.
ケンは柵を修理していました。
英検2級といっても、スピーキングテストの内容は、中学英語レベルです。
しかし、その中学英語がとっさには出てこないことがあります。
そこで、黙り込んでしまうのです。
英語によるコミュニケーション能力を問われているテストで、黙り込むのが一番まずい・・・。
「・・・どうしました?」
「校庭って、英語で何と言いますか?」
「school ground で良いですが、そもそも、そんなことは言わなくても大丈夫ですよ。彼らは、何と遊んでいるの?」
「・・・遊ぶって、英語で何と言いますか?」
「play です」
「・・・ウサギって、英語で何と言いますか?」
「rabbit です」
「・・・They playing rabbit.」
「・・・・」
簡単な単語が出てこないことに動揺してしまうからか、中学英語の文法もめちゃめちゃになっていくのです。
そのまま、3コマ目に行こうとするので、
「ケンの様子も説明してください」
「・・・できません」
「何がわからない?」
「柵」
「a fence」
「ああ!修理する、は?」
「fix」
「ああ・・・」
言われれば意味のわかる単語ばかりなのですが、自分で思いつくことができないのです。
読んだり聞いたりしたときに意味のわかる単語を「理解語彙」といいます。
一方、自ら使うことのできる単語は「使用語彙」です。
ネイティブでも、理解語彙は広いけれども、使用語彙はそのごく一部で、狭い。
知っているけれど使えない単語のほうが圧倒的に多いものです。
まして外国語となると、そもそも理解語彙も狭いのに、使用語彙はさらに狭い。
それを広くするための日頃の練習も特に行っていない・・・。
スピーキングは苦手だから、スピーキングは普段やらない。
そういう英語学習をしてしまう中学生・高校生は多いです。
その一方で、英検受検に関して、ためらいはない。
入試に有利だから。
学校の先生が勧めるから。
そういう理由で気軽に申し込んでしまうのですが、スピーキングの練習をしていないのに英検を受けるので、苦戦してしまいます。
3コマ目の模範解答は。
③ Thirty minutes later, the children were washing their hands.
30分後、子どもたちは手を洗っていました。
Ken was thinking of reading a book to them.
ケンは彼らに本を読むことを考えていました。
英検2級とはいえ、これも、中学英語です。
しかし、またも沈黙してしまう子もいます。
「・・・どうしました?」
「手を洗うって、何と言いますか」
「wash 誰々's hands です」
「・・・They washing they hand.」
「・・・」
文法ミスは、指摘するほど動揺してしまうので、もう目をつぶることにします。
それでも、また沈黙。
「・・・何がわからないですか」
「読み聞かせるって・・・」
「read a book to 誰々」
「・・・He reading book children.」
「・・・」
テンパってしまっていて、普段ならできることもできなくなっています。
塾での模擬面接でこれなので、本番はもっととんでもないことになるのかもしれません。
なぜ、主語の後に動詞をすぐing 形にするのだろう?
冠詞や前置詞が全く出てこなくなるのはなぜなのか。
いや、そもそも基本的な動詞や名詞が出てこないのが深刻だ・・・。
スピーキングが苦手な子の多くは、そうです。
読めばわかる単語も、自分からは使えないのです。
二次面接は、3コマ漫画を英語で説明するだけでは終わりません。
この後、英問英答もあります。
3級なら、「次の週末に何をする予定ですか」程度の易しい問に答えるだけですが、2級ともなれば、社会問題を問われます。
例えば、
Some people say that people in Japan spend too much time at work. What do you think about that?
日本人は働くことに時間を使いすぎると言う人もいます。あなたはそれについてどう思いますか。
これは、日本語で問われても、黙り込んでしまう高校生もいるかもしれません。
社会問題に関心がないので、そんなことを問われても、何の意見もない。
自分には関係ないことだから、考えたことがない。
急に問われても、わからない。
それが正直なところでしょう。
しかし、何か意見を言わなければならない。
身構えてしまい、何か高度なことを言おうとして、かえって言葉が出てこなくなり、黙り込む・・・。
そういうことなのだろうと思うのです。
英検2級で要求されている意見なんて、そんなに高度なことではないのです。
模範解答としては、
I agree. Many companies give their workers too much to do. People don't get enough time to be with their families.
賛成です。多くの会社は労働者にやるべきことを与えすぎです。人々は家族と過ごす十分な時間がありません。
社会問題を論じているようでいても、一歩も先に進んでいません。
状況を説明しているだけです。
でも、それでいいのです。
社会問題を解決する策を提案せよ、と言われているわけではないのですから。
でも、身構えてしまった子は、何か解決策を出さなければならないと思ってしまうのかもしれません。
そして、何か難しいことを言おうとすると、英語が出てこない人も多いです。
長時間労働の弊害って、英語でどう言えばいいんだろう?
従業員って、何て言うんだっけ・・・。
残業って、何て言うんだっけ・・・。
過労死って、何て言うんだっけ・・・。
日本語は思いつくけれど、英語にできないことばかり・・・。
しかし、それで当たり前なのです。
英検2級なんて、ネイティブとしては子どもの英語力です。
だから、むしろ、英語力のある小学生のほうが英検2級には簡単に合格することがあります。
本人の日本語力と英語力が一致していて、落差がないので、言いたいことを英語にできずに言葉に詰まるということが少ないのでしょう。
言いたいことがそもそも幼いので、幼い英語力で済むのです。
一方、高校生は、日本語としてはそれなりに難しい熟語を使ったりします。
それを英語にできないことが多いのです。
自分の日本語を英語に転換できないのです。
ここで重要なのは、表現のレベルを下げること。
自分が英語で語れることのレベルを自覚すること。
ただ、それもまた、普段練習しているから把握できることであり、1次試験の合格通知が届いてから急に練習しても、間にあいません。
器用な人、そもそもの英語力が高い人は、それでも何とか合格圏内に滑り込めますが、スピーキングに自信がない人は、かなり前から準備をしたほうがいいのです。
塾での模擬面接も有効ですし、自学するならば、過去問を使って、回答したいことを紙に書いてみてください。
時間無制限で。
それは、なかなか英語が出てこないことを自覚するためでもあります。
自分が言いたいことを、時間をかけて英語で書くことすら、思うようにいかない。
何て不自由なんだろう。
自分の英語力は、こんな程度なのか。
それを自覚することで、次のステップに進めます。
易しい言葉で、難しいことを語る。
それは可能なことです。
言いたいことのレベルを自分の英語力まで下げていくのが、合格への近道です。
言いたいことのレベルに自分の英語力を上げるのも重要ですが、それには、時間がかかります。
言いたいことを思うように英語にできないことを自覚したら、模範解答の日本語訳を見て、それを英語に直す練習から始めると良いと思います。
模範解答のレベルを知るためでもありますし、答え方のコツをつかむ練習でもあります。
何回かやってみると、解答のパターンがつかめてきます。
こういうふうに応えればいいだけか、とわかってきます。
また、二次試験前だけでなく、日頃から、英語を口に出して言ってみる練習が有効です。
NHKラジオ「英会話タイムトライアル」は、平日の毎日10分で、英語を口に出して言ってみる練習ができます。
「ラジオ英会話」も、前半はその日のスキットの内容解説ですが、後半、毎回2~3問、日本語を英語に直す練習があります。
英検などのスピーキングテストと形式が違うとか、傾向が違うとかには、こだわらないことです。
とっさに英語が出てこない・・・。
その悩みを解決するための練習です。
瞬発力を養いましょう。
2025年02月12日
規則性の問題。受験算数・中学数学。
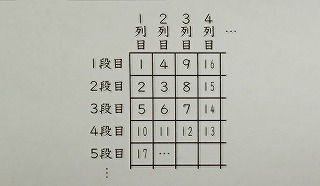
問題 上の図のように数字を並べる。125は、何段目の何列目になるか。
小学生対象の受験算数でも、中学数学でも、規則性の問題として、典型題です。
都立高校の入試問題の大問2でも、こうした規則性を理解した上で式を立てる問題が出題されることがあります。
これは、頭の柔らかさが問われる問題です。
頭が固くて、1度目は何も思いつかないのであれば、せめて、その解き方を理解し、記憶し、以後、似たような問題でそれを利用できるようにしたいものです。
「この問題は、どういうルールで数字が並んでいるんでしょうか」
そう問いかけて、上手く説明できる子は、コミュニケーション能力の高い子です。
ルールをぼんやりと理解しているけれど、それを説明しようとすると上手く言葉にできない。
小・中学生ならば、それで普通です。
1段目の1列目に「1」があります。
その周りをとぐろを巻くように、「2・3・4」が取り巻き、さらのその周りをとぐろを巻くように、「5・6・7・8・9」が取り囲んでいる・・・。
こういう表現を小・中学生ができる可能性は低いですし、その表現ができることが問題を解くことに直接つながるわけでもありません。
表現はできないけれど、そういうルールだと理解できていれば、十分です。
では、問題を解くには、どうすればいいのか?
「とぐろを巻く」ではなく、算数・数学として考えるには、どうすればいいのか?
1段目に着目しましょう。
1段目の数字は、左から順に、
1,4,9,16,25,・・・
この数列の規則性は?
これが重要です。
ここで、頭が固いか柔らかいかを問われます。
そして、このルールは、規則性に関する他の問題でも繰り返し出てきます。
それなのに、規則性というと、「差を読む」発想しかもてない子が多いのです。
規則性は全部等差数列だと思い込んでいます。
そういう問題を沢山解いたせいで、全部そういう問題、という思い込みが強いのかもしれません。
上の数列の差を読むと、
3,5,7,9,・・・
これは、差が一定ではありませんから、等差数列ではないのです。
でも、よく見ると、この差は、等差数列・・・。
これは、高校生になれば、階差数列の考え方で処理できますが、小学生には手に余ります。
もっと、簡単な規則はないのでしょうか?
1,4,9,16,25,・・・
ここの発想力です。
差を読むのではなく、その数字1つ1つに何かルールがないか?
頭が柔らかければ、思いつくのです。
そう。
・・・これは、何かの2乗の数なのです!
1は1×1
4は2×2
9は3×3
16は4×4
数字がそれまでの数を取り巻いて正方形を作るごとに、また下に戻って、さらに外側を取り巻いていく。
このルールに気づいたとき、つまり、正方形を作っているのだから、その段階で、□×□の個数の数字が使われているのです。
このルールを見抜ければ、あとは簡単。
問題は、125が何段目の何列目か。
しかし、125は、□×□で表される数ではありません。
ですから、125に近い数で、そういう数字、すなわち「平方数」を考えます。
「125に近くて、□×□の答になる数字は、何でしょうか」
「62.5」
「・・・62.5?どんな式で求めましたか?」
「・・・125÷2」
「うーん・・・」
2乗と2倍の区別がつかない子は、中学数学に進んでも一定数いますから、小学生のこの発想は責められません。
しかし、一度これで頭が凝り固まると厄介でもあります。
中学生になっても、繰り返し、繰り返し、2乗と2倍を混同する子もいます。
4^2=8 といった誤答を繰り返します。
さらに悪化すると、4×2=16 と答える子もいます。
「62.5×62.5は、125になりますか?元の式にあてはめて、考えてみてください」
しかし、このような指示の意味がよくわからず、混乱していく子もいます。
何を説明されているのか、文脈がつかめないようです。
その誤答がなぜ誤答なのかを説明されているということが理解できず、正解のためのヒントを出されていると思うようです。
意思の疎通が難しい子の多くは、相手の文脈とは違う文脈でものを考えています。
コンピュータを相手にするように、冷静に一歩ずつ伝達していく必要があります。
理解力がないのではないのです。
文脈がずれているのです。
それはさておき。
□×□の答で、125に近いものは何か?
中学受験生として標準的な学力を持っている子は、15×15くらいまでのかけ算の答を覚えていることが多いです。
覚えなさい、と強制されたのではなくても、円の面積を求める問題などで繰り返し計算した結果、何となく覚えてしまっているのです。
塾で強制的に暗記させられた子は、20×20くらいまでは覚えています。
さて、そうした同じ数どうしのかけ算で、125に近い答になるのは?
11×11=121
ですね。
ということは、121は、上の表の、1段目の11列目の数字です。
あとは、実際に指折り数えていったほうが速いです。
12段目の1列目が122。
12段目の2列目が123。
12段目の3列目が124。
12段目の4列目が125。
よって、正解は、12段目の4列目、です。
さて、これを、中学生として式に表す場合。
都立高校入試の大問2では、a、b を用いて、規則性のある数を式で表す問題が出されることがあります。
表中の数字を、a 段目の b 列目として、式を立てるのです。
これもまた、上のように、1段目が平方数であることに気がつけば、立式できます。
1段目の a 列目の数は、a^2です。
ここまでで、a×a の正方形の形に数が埋まっています。
よって、その次の数、すなわち(a+1)段目の1列目の数は、a^2+1です。
したがって、(a+1)段目のb列目の数は、a^2+b と表されます。
125は、何段目の何列目になるのか?
a^2+b=125
と表すことができます。
これに具体的な数をあてはめて、
11^2+4=125
という関係を発想して、
正解は、12段目の4列目、と答えることが可能です。
さて、最後に、高校数B「数列」の考え方で、この問題を解いてみますが、かえって難しくなるだけなので、あまりお勧めしません。
上の考え方のほうがシンプルで良いと思います。
一応やってみましょう。
まずは、とぐろを巻いている数列を、1周目、2周目として、群数列を考えてみます。
(1) , (2,3,4) , (5,6,7,8,9) , (10,11,12,13,14,15,16) , (17,18,19,・・・
この数列で、125は、第何群の何番目でしょうか。
各群の項の個数を考えましょう。
第1群から順に、
1,3,5,7,9,・・・
これは、等差数列です。
第n群までの個数の和を、等差数列の和の公式にあてはめて考えます。
初項1、公差2の等差数列の、第n項は、
1+2(n-1)
=2n-1
ですから、第n項までの和は、
1/2n(1+2n-1)
=n^2
よって、この群数列において、第n群までの項の総数はn^2となります。
群数列として分割する前のもとの数列は、自然数の数列ですので、総数n^2が、そのまま、その項の数字となります。
したがって、第n群の最終項は、n^2です。
その1つ前の第(n-1)群の最後の数字は、(n-1)^2と表されます。
125は、第n群の数字なのですから、
(n-1)^2<125≦n^2
という不等式が成り立ちます。
11^2=121、12^2=144より、
n=12
よって、125は、第12群の数です。
ここで、第11群の最後の項は121ですから、第12群の最初の項は、122。
125は、第12群の4番目となります。
数の表のように数字をあてはめた場合、第12段の4列目。
ただし、これは、もしも第12群の14番目などの数字の場合は、第12段の位置ではなくなってしまうことに注意が必要です。
簡単なことが、何か面倒くさかったですね。
さらに面倒くさい解き方をしてみましょうか。
1段目の数字に着目して、大真面目に高校数学で解いてみると、
1,4,9,16,25,・・・
これは、等差数列でも等比数列でもありません。
しかし、上の数列の差を読む、すなわち、階差数列を考えると、
3,5,7,9,・・・
これは、初項3、公差2の等差数列です。
この階差数列の第n項は、
3+2(n-1)
=2n+1
となります。
よって、元の数列の第n項は、
1+Σ(2k+1)
となります。
ここで、Σの下はk=1、上は、k=n-1 です。
つまり、初項から第(n-1)項までの階差数列の和を、もとの数列の初項1にたしたものが、もとの数列の一般項です。
公式を利用して、計算してみましょう。
1+2・1/2(n-1)・n+n-1
=1+n^2-n+n-1
=n^2
やはり、この数列の第n項は、n^2なのです。
見たらすぐわかることを、異様に難しく解いてしまいました・・・。
つまるところ、
1,4,9,16,25,・・・
という数列を見たときは、2乗だ、平方数だ、とすぐに気づいたほうが簡単です。
最初に発想できなかったら、こういうことがあるのだと、知識として頭の中に入れておきましょう。
それで解くことのできる問題に、必ず再び出会います。
小学生対象の受験算数でも、中学数学でも、規則性の問題として、典型題です。
都立高校の入試問題の大問2でも、こうした規則性を理解した上で式を立てる問題が出題されることがあります。
これは、頭の柔らかさが問われる問題です。
頭が固くて、1度目は何も思いつかないのであれば、せめて、その解き方を理解し、記憶し、以後、似たような問題でそれを利用できるようにしたいものです。
「この問題は、どういうルールで数字が並んでいるんでしょうか」
そう問いかけて、上手く説明できる子は、コミュニケーション能力の高い子です。
ルールをぼんやりと理解しているけれど、それを説明しようとすると上手く言葉にできない。
小・中学生ならば、それで普通です。
1段目の1列目に「1」があります。
その周りをとぐろを巻くように、「2・3・4」が取り巻き、さらのその周りをとぐろを巻くように、「5・6・7・8・9」が取り囲んでいる・・・。
こういう表現を小・中学生ができる可能性は低いですし、その表現ができることが問題を解くことに直接つながるわけでもありません。
表現はできないけれど、そういうルールだと理解できていれば、十分です。
では、問題を解くには、どうすればいいのか?
「とぐろを巻く」ではなく、算数・数学として考えるには、どうすればいいのか?
1段目に着目しましょう。
1段目の数字は、左から順に、
1,4,9,16,25,・・・
この数列の規則性は?
これが重要です。
ここで、頭が固いか柔らかいかを問われます。
そして、このルールは、規則性に関する他の問題でも繰り返し出てきます。
それなのに、規則性というと、「差を読む」発想しかもてない子が多いのです。
規則性は全部等差数列だと思い込んでいます。
そういう問題を沢山解いたせいで、全部そういう問題、という思い込みが強いのかもしれません。
上の数列の差を読むと、
3,5,7,9,・・・
これは、差が一定ではありませんから、等差数列ではないのです。
でも、よく見ると、この差は、等差数列・・・。
これは、高校生になれば、階差数列の考え方で処理できますが、小学生には手に余ります。
もっと、簡単な規則はないのでしょうか?
1,4,9,16,25,・・・
ここの発想力です。
差を読むのではなく、その数字1つ1つに何かルールがないか?
頭が柔らかければ、思いつくのです。
そう。
・・・これは、何かの2乗の数なのです!
1は1×1
4は2×2
9は3×3
16は4×4
数字がそれまでの数を取り巻いて正方形を作るごとに、また下に戻って、さらに外側を取り巻いていく。
このルールに気づいたとき、つまり、正方形を作っているのだから、その段階で、□×□の個数の数字が使われているのです。
このルールを見抜ければ、あとは簡単。
問題は、125が何段目の何列目か。
しかし、125は、□×□で表される数ではありません。
ですから、125に近い数で、そういう数字、すなわち「平方数」を考えます。
「125に近くて、□×□の答になる数字は、何でしょうか」
「62.5」
「・・・62.5?どんな式で求めましたか?」
「・・・125÷2」
「うーん・・・」
2乗と2倍の区別がつかない子は、中学数学に進んでも一定数いますから、小学生のこの発想は責められません。
しかし、一度これで頭が凝り固まると厄介でもあります。
中学生になっても、繰り返し、繰り返し、2乗と2倍を混同する子もいます。
4^2=8 といった誤答を繰り返します。
さらに悪化すると、4×2=16 と答える子もいます。
「62.5×62.5は、125になりますか?元の式にあてはめて、考えてみてください」
しかし、このような指示の意味がよくわからず、混乱していく子もいます。
何を説明されているのか、文脈がつかめないようです。
その誤答がなぜ誤答なのかを説明されているということが理解できず、正解のためのヒントを出されていると思うようです。
意思の疎通が難しい子の多くは、相手の文脈とは違う文脈でものを考えています。
コンピュータを相手にするように、冷静に一歩ずつ伝達していく必要があります。
理解力がないのではないのです。
文脈がずれているのです。
それはさておき。
□×□の答で、125に近いものは何か?
中学受験生として標準的な学力を持っている子は、15×15くらいまでのかけ算の答を覚えていることが多いです。
覚えなさい、と強制されたのではなくても、円の面積を求める問題などで繰り返し計算した結果、何となく覚えてしまっているのです。
塾で強制的に暗記させられた子は、20×20くらいまでは覚えています。
さて、そうした同じ数どうしのかけ算で、125に近い答になるのは?
11×11=121
ですね。
ということは、121は、上の表の、1段目の11列目の数字です。
あとは、実際に指折り数えていったほうが速いです。
12段目の1列目が122。
12段目の2列目が123。
12段目の3列目が124。
12段目の4列目が125。
よって、正解は、12段目の4列目、です。
さて、これを、中学生として式に表す場合。
都立高校入試の大問2では、a、b を用いて、規則性のある数を式で表す問題が出されることがあります。
表中の数字を、a 段目の b 列目として、式を立てるのです。
これもまた、上のように、1段目が平方数であることに気がつけば、立式できます。
1段目の a 列目の数は、a^2です。
ここまでで、a×a の正方形の形に数が埋まっています。
よって、その次の数、すなわち(a+1)段目の1列目の数は、a^2+1です。
したがって、(a+1)段目のb列目の数は、a^2+b と表されます。
125は、何段目の何列目になるのか?
a^2+b=125
と表すことができます。
これに具体的な数をあてはめて、
11^2+4=125
という関係を発想して、
正解は、12段目の4列目、と答えることが可能です。
さて、最後に、高校数B「数列」の考え方で、この問題を解いてみますが、かえって難しくなるだけなので、あまりお勧めしません。
上の考え方のほうがシンプルで良いと思います。
一応やってみましょう。
まずは、とぐろを巻いている数列を、1周目、2周目として、群数列を考えてみます。
(1) , (2,3,4) , (5,6,7,8,9) , (10,11,12,13,14,15,16) , (17,18,19,・・・
この数列で、125は、第何群の何番目でしょうか。
各群の項の個数を考えましょう。
第1群から順に、
1,3,5,7,9,・・・
これは、等差数列です。
第n群までの個数の和を、等差数列の和の公式にあてはめて考えます。
初項1、公差2の等差数列の、第n項は、
1+2(n-1)
=2n-1
ですから、第n項までの和は、
1/2n(1+2n-1)
=n^2
よって、この群数列において、第n群までの項の総数はn^2となります。
群数列として分割する前のもとの数列は、自然数の数列ですので、総数n^2が、そのまま、その項の数字となります。
したがって、第n群の最終項は、n^2です。
その1つ前の第(n-1)群の最後の数字は、(n-1)^2と表されます。
125は、第n群の数字なのですから、
(n-1)^2<125≦n^2
という不等式が成り立ちます。
11^2=121、12^2=144より、
n=12
よって、125は、第12群の数です。
ここで、第11群の最後の項は121ですから、第12群の最初の項は、122。
125は、第12群の4番目となります。
数の表のように数字をあてはめた場合、第12段の4列目。
ただし、これは、もしも第12群の14番目などの数字の場合は、第12段の位置ではなくなってしまうことに注意が必要です。
簡単なことが、何か面倒くさかったですね。
さらに面倒くさい解き方をしてみましょうか。
1段目の数字に着目して、大真面目に高校数学で解いてみると、
1,4,9,16,25,・・・
これは、等差数列でも等比数列でもありません。
しかし、上の数列の差を読む、すなわち、階差数列を考えると、
3,5,7,9,・・・
これは、初項3、公差2の等差数列です。
この階差数列の第n項は、
3+2(n-1)
=2n+1
となります。
よって、元の数列の第n項は、
1+Σ(2k+1)
となります。
ここで、Σの下はk=1、上は、k=n-1 です。
つまり、初項から第(n-1)項までの階差数列の和を、もとの数列の初項1にたしたものが、もとの数列の一般項です。
公式を利用して、計算してみましょう。
1+2・1/2(n-1)・n+n-1
=1+n^2-n+n-1
=n^2
やはり、この数列の第n項は、n^2なのです。
見たらすぐわかることを、異様に難しく解いてしまいました・・・。
つまるところ、
1,4,9,16,25,・・・
という数列を見たときは、2乗だ、平方数だ、とすぐに気づいたほうが簡単です。
最初に発想できなかったら、こういうことがあるのだと、知識として頭の中に入れておきましょう。
それで解くことのできる問題に、必ず再び出会います。
2025年02月12日
春期講習のお知らせ。2025年。
2025年、春期講習のお知らせです。
詳細は、書面にしてお渡しいたします。
申し込みは、3月1日(土)からとなります。
日付が変わった深夜12時からお申込み可能です。
メール・LINEまたは申込書でお申込みください。
なお、この期間、通常授業はありませんので、いつもの時間帯の授業を希望される方も改めてお申込みください。
外部生の募集もいたします。
引き続き、教室ではマスク着用をお願いいたします。
感染対策を万全に行い、安心して学習できる環境を整えております。
以下は、春期講習募集要項です。
◎期日
3月24日(月) ~4月5日(土)
ただし日曜日は休校といたします。
◎時間帯
10:00~11:30 , 11:40~13:10 , 13:20~14:50 , 15:00~16:30 , 16:40~18:10 , 18:20~19:50 , 20:00~21:30
◎形式
完全1対1の個別指導となります。
◎費用
1コマ90分4,000円×受講回数
◎指導科目
小学生 一般算数・受験算数・英語
中学生 数学・英語・国語
中3都立受験生に限り、理科・社会
高校生 数学・英語
2025年02月05日
勉強のやり方を教えてくれる英語長文。

英語長文読解問題を読むことは、読書体験としても有意義ものである場合があります。
例えば、こんな長文。
Research shows that tests often play at least as important a role as the class itself. In one study, they asked students to memorize words in a fixed amount of time, but with several different strategies. One group was told to spend all their time studying, in eight short sessions. A second group received six sessions of studying, interrupted by two tests. Finally, the third group alternated four brief study sessions and four tests. Because all three groups had the same amount of time, testing actually reduced the time available for studying. Yet the results were clear: forty-eight hours later, the students' memory of the word list was better, the more opportunities they had to test themselves. Regularly exchanging periods of studying and testing forced them to engage and receive explicit feedback. Such self-awareness is useful because it allows the learner to focus harder on the difficult items during the subsequent study sessions. The more you test yourself, the better you remember what you have to learn.
The paradox is that students are not aware of these effects. They think that testing is a distraction, and that studying what matters. And in agreement with this wrong idea, most students voluntarily spend their time reading class notes and textbooks, highlighting ech line with a different color of the rainbow... all strategies that are much less effective than taking a brief test.
問題1. 上の英文と内容が一致するものを以下の①~④から1つ選び、その番号を答えなさい。
① 3つのグループとも同じ総時間が与えられたが、どのグループでも勉強時間を増やすために、テスト時間を減らした。
② 3つのグループとも同じ総時間が与えられたが、その中でテスト時間を設けたグループでは、その分勉強時間が減った。
③ 3つのグルーブとも同じ勉強時間が与えられたので、テスト時間も追加されたグループは総時間が長くなった。
④ 3つのグループともそれぞれ同じ勉強時間とテスト時間が与えられた。
問題2. 上の英文から考えられるテストの効果として最も適切なものを以下の➀~④から1つ選び、その番号を答えなさい。
① テストは、知識や能力の測定結果をもたらしてくれる。
② テストは、成績評価のための基礎データをもたらしてくれる。
③ テストは、勉強への動機づけをもたらしてくれる。
④ テストは、学んだことを思い出させてくれる。
さて、今回も、わからない単語は英語のまま、訳してもらいました。
第1文
Research shows that tests often play at least as important a role as the class itself.
「研究者たちは示す / テストはしばしば重要な役割を果たす / 少なくとも授業自体と同じくらい」
「はい。すばらしい」
第2文。
In one study, they asked students to memorize words in a fixed amount of time, but with several different strategies.
「ある研究では、彼らは生徒たちに頼んだ / 単語を記憶するように / 修理された量の時間で / しかし、いくつかの異なるストラテジーで」
「fix は、ここでは『修理する』という意味ではありません。fix のままで」
第3文。
One group was told to spend all their time studying, in eight short sessions.
「1つのグループは、言われた / 全ての時間を勉強に使うように / 8個の短いセッションの中で」
第4文。
A second group received six sessions of studying, interrupted by two tests.
「2つ目のグループは、受けた / 勉強の6個のセッションを / 2つのテストにインターラプトされて」
第5文。
Finally, the third group alternated four brief study sessions and four tests.
「最後に、3番目のグループは、オルターネイトした / 4つの短い勉強セッションと4つのテストを」
第6文。
Because all three groups had the same amount of time, testing actually reduced the time available for studying.
「すべての3つのグループは同じ量の時間を持っていたから、テストは実際は減らした / 時間を / 勉強に利用可能な」
「いいですね」
第7文。
Yet the results were clear: forty-eight hours later, the students' memory of the word list was better, the more opportunities they had to test themselves.
「しかし、結果は明らかだった。48時間後、生徒たちの単語リストの記憶はより良かった / より多くの機会 / 彼らが自分自身にテストしなければならないほうが」
第8文。
Regularly exchanging periods of studying and testing forced them to engage and receive explicit feedback.
「定期的に勉強とテストの期間を交換することが、彼らにエンゲージさせ、受け取らせた。エクスプリクトなフィードバックを」
第9文。
Such self-awareness is useful because it allows the learner to focus harder on the difficult items during the subsequent study sessions.
「そのような、セルフ・アウェアネスは、役に立つ / なぜなら、それは学習者に許す / より一所懸命集中することを / 異なるものに / サブシーケントな学習セッションを」
第10文。
The more you test yourself, the better you remember what you have to learn.
「より多く自分でテストすればするほど、よりよく覚える / 学ばなければならないことを」
「すばらしい」
第11文。
The paradox is that students are not aware of these effects.
「パラドックスは、生徒たちがこれらの影響を知らないことだ」
第12文。
They think that testing is a distraction, and that studying what matters.
「彼らは、テストはデストラクションで、勉強がホワット・マターだと思っている」
第13文。
And in agreement with this wrong idea, most students voluntarily spend their time reading class notes and textbooks, highlighting ech line with a different color of the rainbow... all strategies that are much less effective than taking a brief test.
「そして、この間違った考えに同意する中で、大部分の生徒は自主的に費やす / 彼らの時間を / 授業ノートや教科書を読むことに / それぞれの行にハイライトする / 虹色の異なる色で・・・ / すべてのストラテジーはあまり影響しない / 短いテストをするよりも」
かなり正確に和訳できていたので、意味をとりやすかったと思います。
わからない単語もありましたが、全体を見通せば、わからない単語など、わからないままでも大丈夫だと実感できる英文です。
特に、実験部分がクリアでしたね。
問題1. 上の英文と内容が一致するものを以下の➀~④から1つ選び、その番号を答えなさい。
① 3つのグループとも同じ総時間が与えられたが、どのグループでも勉強時間を増やすために、テスト時間を減らした。
② 3つのグループとも同じ総時間が与えられたが、その中でテスト時間を設けたグループでは、その分勉強時間が減った。
③ 3つのグルーブとも同じ勉強時間が与えられたので、テスト時間も追加されたグループは総時間が長くなった。
④ 3つのグループともそれぞれ同じ勉強時間とテスト時間が与えられた。
第6文。
Because all three groups had the same amount of time, testing actually reduced the time available for studying.
「すべての3つのグループは同じ量の時間を持っていたから、テストは実際は減らした / 時間を / 勉強に利用可能な」
とありました。
したがって、正解は、②です。
問題2. 上の英文から考えられるテストの効果として最も適切なものを以下の①~④から1つ選び、その番号を答えなさい。
① テストは、知識や能力の測定結果をもたらしてくれる。
② テストは、成績評価のための基礎データをもたらしてくれる。
③ テストは、勉強への動機づけをもたらしてくれる。
④ テストは、学んだことを思い出させてくれる。
一般論としては、どの選択肢も正しいですが、この英文から考えられるものとして最も適切なものは、どれでしょう。
第10文。
The more you test yourself, the better you remember what you have to learn.
「より多く自分でテストすればするほど、よりよく覚える / 学ばなければならないことを」
とありました。
したがって、正解は、④です。
さて、この英文、入試で初めて読むのではなく、それよりももっと早い段階で読んでおきたい内容です。
自分にテストをすることの大切さ。
それによる記憶の定着。
それを知っているだけで、学習の能率が上がります。
当たり前のことのようで、勉強が苦手な子ほど、これを知らないのです。
あるいは、うすうす気づいているけれど、自分にテストをして、全くできない自分を自覚するのが嫌なので、自分へのテストを避けてしまい、ひたすらノートや教科書を読むだけの勉強をしてしまいます。
実験結果も明らかなことなのですから、能率の悪い勉強をやめて、自分へのテストを繰り返しましょう。
The paradox is that students are not aware of these effects.
「逆説的なことは、生徒たちがこれらの影響を知らないということだ」
They think that testing is a distraction, and that studying what matters.
「彼らは、テストは気を散らすもので、勉強が重要なことだと思っている」
And in agreement with this wrong idea, most students voluntarily spend their time reading class notes and textbooks, highlighting ech line with a different color of the rainbow... all strategies that are much less effective than taking a brief test.
「そして、この間違った考えにしたがって、ほとんどの生徒は、授業ノートや教科書を読むことや、それぞれの行を虹色のマーカーで塗ることに時間を費やす・・・ 。それらの戦略は短いテストをするよりも効果がはるかに少ない」
重要なところをマーカーで塗ったらダメだとは言わないのですが、マーカーで塗っただけで満足し、それで勉強した気になるのは無意味です。
マーカーで塗ったら、塗ったところを覚えて、塗ったところを自分でテストしましょう。
勉強が得意な子が当たり前にやっているのに、勉強が苦手な子がどうしてもできないことは、案外こんなことです。
気持ちで負けてしまい、楽な勉強に逃げてしまうのです。
頑張りましょう。
2025年01月25日
中1数学「比例・反比例」の活用の問題。

「活用」の問題とは、数学の問題を、実生活と結びつけて考えてみるものです。
目的の1つは、生徒が数学に興味を持つようになることでしょう。
しかし、実際は、数学がますます難しく感じられ、苦手になっている場合が多いのです。
中1数学の「比例・反比例」を例にとって考えてみましょう。
例えば、こんな問題。
問題 視力検査に使われる、1か所が切れている輪が描かれた図形は、ランドルト環と呼ばれる。
外周直径7.5mm、切れ目1.5mmのランドルト環を5.0m離れた場所から見て、切れ目の方向がはっきり見えれば「視力1.0」と定められている。
ランドルト環の大きさをいろいろと変えて、5.0m離れた場所から視力を測るとき、視力はランドルト環の外周直径に反比例するものとして、以下の問いに答えなさい。
(1) ランドルト環の外周直径が12.5mmのときの視力を求めなさい。
(2) 視力が1.5のとき、外周直径が何mmのランドルト環まで明瞭に見えるか。
基本問題は正解できるのに、こういう問題になると、頭が真っ白になる・・・。
日本の過半数の生徒がそうかもしれません。
自力では、こういう問題は解けないのです。
実際の問題には、ランドルト環の図も添えられていて、よりわかりやすくなっています。
それでも、わからない・・・。
原因は色々と考えられます。
①知らない事柄が問題に出されると、「知らない」「わからない」「習っていない」と短絡的に反応してしまう。
②問題を読み取る力が低い。
③知識の応用が効かない。
まず①について。
この問題を宿題に出したところ解けなかった子に授業をしたときのこと。
「何がわからないですか?」
「・・・ランドルト環」
「そうですか。でも、視力検査でこの図形を見たことはありますよね?私も、そういえばそんな名前を聞いたことがある、という程度ですが」
「・・・」
「ランドルト環のことを知らなくても、この問題は解けますよ」
「・・・」
しかし、多くの生徒は、知らないことが問題に出されたら、知らないから解けない、となってしまいます。
この頭の固さは、どうすれば改善できるのか・・・。
頭が柔軟な子は、このタイプの問題を何問か解いていくうちに、知らないことであっても問題を解くのには支障がないことを実感し、解いていけるようになります。
本人の中に学習能力が備わっているので、新しいことへの対応の仕方も学習していきます。
しかし、そうはならない子も多いのです。
とにかく頭が固い。
「活用」のどの問題も、結局自力では解けず、解説を聞いて、あるいは解説を読んで、その解き方を覚え込むだけとなるのです。
実際にテストに出るのは、また別の初見の問題。
「活用」の問題に、典型題は存在しません。
初めて見る内容ばかりです。
そうであるのに、「知らないことは、わからない」。
そうやって、固まってしまいます。
頭の固さの改善は、一朝一夕にはいきません。
究極、学ぶことで頭を柔らかくしていくしか、道はありません。
自分の頭の固さという課題を自覚して、一歩一歩進んでいくしか道はないのだと思います。
知らない事柄でも、数学の問題は解ける!
まず、落ち着いて、そのことを意識することです。
②問題を読み取る力が低い。
については、どうでしょうか。
「問題に、反比例という言葉がありますよ。何と何が反比例するのか、読み取れますか」
「・・・」
非常に不思議な傾向なのですが、読解力の低い子に、このように話しかけたとき、私をまっすぐに見つめ返すけれど、問題文には目を戻さないことが多いのです。
私の顔なんか見たところで、何も書いていないのに。
人が話しているときには、人の目を見ましょう。
そういう教育が行き届いているのでしょうか?
それもあるのでしょうが、おそらく、「問題文をもう一度読みなさい」という指示を私が出していないことが一因なのだろうと思います。
文字を読むだけでなく、人の話を聞く上での「読解力」も低い子は、直截に具体的な指示を出さないと、何を期待されているか理解できないことがあります。
「問題をもう一度見て、読み取りましょう。何と何が反比例するのでしょう。問題文に書いてありますね」
「・・・視力は、ランドルト環の外周直径に反比例する」
「そうです。今、1組、具体的な値が問題文に載っています。問題文を見直してください。視力がいくつのとき、ランドルト環の外周直径はいくつですか」
「7.5のとき、1.5」
「・・・違いますよ」
「7.5のとき5」
「・・・違います」
こういう「活用」の文章題では、不要な数値が他に多く書かれていることがあります。
そうした中で、必要な数値がどれなのか読み取れない生徒がいます。
1つ1つ、補助していく必要があります。
「視力はいくつですか。読み取ってください」
「・・・・1.0?」
「そうです。そのときの、ランドルト環の外周直径は?」
「5?」
「違います」
「1.5?」
「違います。・・・落ち着いて。即答しなくていいんですよ。ゆっくり読み取って。何分かかってもいいんです。大切なのは、正解すること」
「・・・・・・・・・7.5?」
「そうです!」
・・・しかし、そうやって一度読み取った数値も、では解きましょうと促したとき、もう忘れていることもあります。
記憶がもたず、本人にメモを取る習慣もありません。
そこは、特に個別指導が必要なところです。
メモを取ろう!
下線を引くか、〇で囲もう!
そのように助言を繰り返しますが、往々にして、そうした助言を受けたこともすぐに忘れます。
幾度も幾度も忠告と助言を繰り返し、年単位の学習の後に、身についていきます。
さて、課題の3つ目。
③知識の応用が効かない。
今までのところは、何だか低学力の子の話だけしているような印象を持たれた方も多いと思いますが、「活用」の問題が解けないのは、低学力の子だけではありません。
ほんのひと握りの秀才以外は、ほおっておいたら「活用」の問題は解けない、と覚悟する必要があります。
それほどに、「活用」は、高く大きな壁です。
知らないことが問題に書いてあっても、問題文の中で知れば大丈夫なのだとわかっている。
それなりに読解力もある。
課題の①や②はクリアしている子たちです。
それなのに、なぜ、大多数の子は、「活用」の問題が解けないのか?
それは、応用力がないからです。
ではなぜ、応用力がないのか?
反比例の基本問題は解くことができても、それは作業手順として覚えているだけで、意味はわかっていないのです。
このことはもう本当に繰り返し書いてきました。
小学生の頃から、算数・数学は、作業手順だけになってしまっている子は多いです。
理由も、繰り返し書いてきました。
ある意味頭の回転が速かったため、意味まで深く理解するような「重い」学習を避け、やり方だけちゃちゃっと覚えることで済ませてきた子。
意味が全く理解できなかったため、やり方を覚えることに活路を見出してきた子。
ある中学生と「方程式」の授業をしていたときのこと。
平均の考え方を使う問題でした。
「平均って、小学校で勉強しましたよね。公式を覚えていますか。平均はどうやって求めるのだったでしょうか」
その子は、長い沈黙の後、答えました。
「・・・たして、割る」
・・・まあ、確かに、その通りですし、語彙が少ない子でしたので、本当はわかっているのに、そのようにしか表現できなかった可能性もありますが、手順しか覚えていないのだし、手順にしか興味がないからこの答になるのだろうとも感じてしまうのです。
では、なぜ手順しか覚えないのか?
意味まで深く理解するような「重い」学習をすると、頭が重くなって苦しくて、脳細胞が潰れる気がするので、そういうことを本能的に避けてしまう子は案外多いです。
こんなに秀才ふうな子がそんなレベルなの?と思うこともあります。
小学校のカラーテストでは毎回90点以上を取っていたのに、実は何もわかっていなかった、ということもあるのです。
理解はすべて表面的。
ただの作業手順です。
とはいえ、意味がわかった上での手順は、数学で通用することでもあります。
問題を分析した後は、手順に沿って、合理的に解いていく。
正解への最短距離をいく。
小学校から作業手順だけだった子は、それができないのです。
基盤がないので、
「ここは、あの公式を使えばいい」
「ここは、あの手順でいい」
という判断が自力でできないし、そのような指示には、逆にポカンとしがちです。
「反比例すると問題に書いてあるのですから、反比例なのですね。ならば、反比例の一般式にあてはめて解くことができますよ」
「・・・」
「反比例の一般式は、覚えていますか」
「・・・y=a / x」
「そうです。その式を使って、解いていきましょう」
「・・・」
この単純な思考を、自力で行うことができないのです。
日頃は何でも作業手順で覚えこもうとするのに、なぜ、この作業手順が理解できないのだろう?
なぜ心も頭もついていけないような様子を見せるのだろう?
そう思うことは多いです。
もう一度問題を見ましょう。
問題 視力検査に使われる、1か所が切れている輪が描かれたものは、ランドルト環と呼ばれる図形である。
外周直径7.5mm、切れ目1.5mmのランドルト環を5.0m離れた場所から見て、切れ目の方向がはっきり見えれば「視力1.0」と定められている。
ランドルト環の大きさをいろいろと変えて、5.0m離れた場所から視力を測るとき、視力はランドルト環の外周直径に反比例するものとして、以下の問いに答えなさい。
(1) ランドルト環の外周直径が12.5mmのときの視力を求めなさい。
(2) 視力が1.5のとき、外周直径が何mmのランドルト環まで明瞭に見えるか。
視力は、ランドルト環の外周直径に反比例する。
では、視力とランドルト環の外周直径の積は、常に一定なのです。
こういうときは、反比例のフォーマルな一般式、y=a / x よりも、
xy=a
という式のほうが、文章題を解くのは楽です。
今、与えられている1組の数値は、外周直径7.5mmで、視力1.0。
この問題の比例定数は、7.5×1.0=7.5
これさえわかれば、何でも解けます。
(1) ランドルト環の外周直径が12.5mmのときの視力を求めなさい。
xy=7.5 ということですから、
これに、x=12.5を代入して、
12.5y=7.5
y=7.5÷12.5
=0.6
求める視力は、0.6 です。
(2) 視力が1.5のとき、外周直径が何mmのランドルト環まで明瞭に見えるか。
xy=7.5
これに、y=1.5を代入して、
1.5x=7.5
x=7.5÷1.5
=5
求める外周直径は、5mmです。
と、小数のままスラスラと解きましたが、方程式の解き方の基本に戻って、全体を10倍してから解いても構いません。
こういう文章題は、特に指示がない場合は必ず割り切れますから、今回は、小数のまま解きました。
このように、「活用」の問題は、文章が長いし、不要な数値も入っていますが、構造は、
問題 y は x に反比例しているとする。x=1のとき、y=7.5である。y=12.5のときの xの値を求めなさい。
という基本問題と同じなのです。
それを見抜くこと。
構造を把握すること。
それが、数学における応用力なのですが、多くの生徒が、この応用力が不足しています。
応用問題を見ると、初めての問題を初めての解き方で解かねばならないと身構えてしまうのでしょうか。
知っていることを全部放り投げてしまいます。
まずは、基本を頭の中にしっかり入れること。
その上で、応用問題は、基本の知識を使うのだと、強く意識することです。
知識が頭の中にあるのに、使えない。
使い方がわからない。
その改善には、経験がものを言います。
問題を解き散らかし、わからないとすぐ解答解説を見て、その問題の解き方を暗記する・・・。
それを繰り返しても、応用力はつかないです。
同じ1時間、数学の勉強をするのならば。
基本が身についていない子は、まず基本の公式を理解し、暗記し、基本問題を沢山解きましょう。
公式も覚えていない、基本問題の解き方も知らない、という状態で「活用」の問題を解くのは、無理です。
しかし、基本は身についている子ならば、応用問題を時間をかけて考え抜きましょう。
1問に1時間かかってもいいです。
もしも、1時間かかって1問を自力で正解すれば、それだけで、応用力は爆上がりします。
その無駄のような1時間の間に、脳細胞が繋がって、繋がって、繋がって、頭の中に様々なバイパスが通るからです。
数学が得意な子、数学が好きな子は、当たり前のようにそれをやっています。
数学の問題を考えていたら、気がつくと2時間経っていた・・・。
そんな夢を見ているような時間の使い方をしているのです。
そして、それは決して無駄な時間ではないのです。
時短とかタイパの話は、よそでやりましょう。
数学の力をつけるときには不要です。
「活用」の問題は、教科書や問題集でも、数が少ない。
貴重な問題なのに、すぐに解答解説を見てわかった気になっても、そっくりな問題はテストには出ません。
構造や本質が見抜けるようにならない限り、全ての問題が見たことのない新しい問題です。
「活用」の問題は、深く考えて応用力を養う、数少ない機会です。
有効に使ってください。
2025年01月18日
高校英語長文読解。基本単語の意味は覚えましょう。

さて今回も、英語長文を読んでいきましょう。
In the early 1900's, Wilhelm von Osten, a German horse trainer and mathematician, told the world that his horse could do math. For years, von Osten traveled Germany giving demonstrations of this phenomenon. He would ask his horse, Clever Hans, to solve simple mathematical equation. In response, Hans would tap his hoof for the correct answer. (A).
Broad public interest in Clever Hans persuaded the German Board of Education to establish a commission to investigate the validity of von Oster's claims about his horse's abilities. The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions. Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers. Then he would stop. When he couldn't see or hear the audience or his trainer, (B).
There's a lot that computer science can learn from Hans today. An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information. Consequently, most types of artificial intelligence are relatively easy to deceive.
問1 空所(A)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. If asked how many digits are in "4321," four taps.
b. If asked the time around noon, twelve taps
c. The numeral "9" refer to what number? Nine taps.
d. The result of dividing eight by two? Four taps.
問2 空所(B)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. he would feel tapping in his heart
b. he would keep tapping and tapping
c. he would start tapping the audience
d. he would tap out the right answer
問3 下線部There's a lot that computer science can learn from Hans today. とあるが、Hans の逸話から、computer science が学べることとは何か。最も適切なものを次のa~dから1つ選びなさい。
a. 賢いふるまいを見せたとしても、称賛してくれる人々がいないのなら意味がない、ということ。
b. 最初は賢くなくても、きちんと訓練すれば、数の計算を正しくできるようになる、ということ。
c. 正しい答を出しているからといって、問題を正しく理解しているとは限らない、ということ。
d . 人々の期待に迎合しすぎると、元々は解けていた問題さえ、正しく解けなくなる、ということ。
今回も、第1文から、わからない単語はわからないまま、生徒に訳してもらったときのこと。
しかし、これが出来るのは、コミュニケーションが取れる子だということも強調したいことです。
わからない英語は英語のままで訳してと幾度促しても、わからない単語が1語あるだけで黙り込んでしまう子もまた多いのです。
それでは英語を読む練習にならないと説得しても、恥ずかしいのか、本人の中で納得できない部分があるのか、黙り込み、私の助けを待ってしまいます。
私が逐語訳をしてあげなければ結局先に進まないので、わからない単語がある中で英文を読んでいく練習になりません。
また、何度説明しても、前から順番に訳さず、日本語らしい順番にしようとして混乱し、その結果黙り込む、という子も多いです。
仕方なく私が訳すと、何だか色々とメモを取ります。
わからなかった単語の意味を書き込んでいるのですが、そんなもの、英文を読み進めていく力にはつながりません。
メモを取っただけで満足してしまう場合が多いのです。
その単語は次回はマスターしている、ということはあまり期待できません。
メモを取ることで勉強した気になってしまうのだと思うのですが、メモを取ることは、勉強ではないのです。
頭に入れることが、勉強です。
真面目なのだけれど勉強が下手な子は、そのように、何か勉強した跡を残したがります。
頭を使わない方向の勉強をしがちです。
単語の意味が知りたかったら、後で、単語集で意味を調べなさい、と繰り返し助言し、何とか自力で読み進めていける方向に指導しています。
単語の意味がわからなくて悔しいのなら、単語暗記をもっと本気でやったらいい。
それと並行して、わからない単語は、わからないまま、読み進める練習も必要。
繰り返しその話をし、わからない単語が1つあるとそこで押し黙ってしまう子も、自力で読み進めていけるよう指導しています。
そんなわけで、第1文。
In the early 1900's, Wilhelm von Osten, a German horse trainer and mathematician, told the world that his horse could do math.
「1900年代初め、ウィルヘルム・バン・オーステン、ドイツの馬のトレイナーでマスマティシャンは、世界に話した。彼の馬は数学ができると」
「・・・はい。mathematician って何でしょうね」
「・・・」
第2文。
For years, von Osten traveled Germany giving demonstrations of this phenomenon.
「何年もの間、バン・オースティンは旅行した。ドイツを。デモンストレーションを与えながら。このポネオネノンを」
「フェノメナンです」
第3文。
He would ask his horse, Clever Hans, to solve simple mathematical equation.
「彼は彼の馬、クレバー・ハンスに尋ねた。単純なマスマティカルなイクエーションを解くことを」
「mathematical って、何ですかね」
「・・・」
第4文。
In response, Hans would tap his hoof for the correct answer. (A).
「返事で、ハンスは彼のひづめをタップした。正しい答のために」
「いいですね」
ひづめは、欄外に、注釈が載っていました。
第5文。
Broad public interest in Clever Hans persuaded the German Board of Education to establish a commission to investigate the validity of von Oster's claims about his horse's abilities.
「ブロードなパブリックの興味、クレバー・ハンスの、は、パースェードした。ジャーマン・ボード・オブ・エデュケーションを。コミッションを設立するように。調べるために。バン・オースティンの主張を。彼の馬についての」
「おお。頑張った!」
第6文。
The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions.
「コミッションは、発見した。クレバー・ハンスは本当は解いていなかった。マスマティカルなイクエーションを。全く。しかし、反応していた。人々のリアクションに」
「うん」
第7文。
Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers.
「ハンスは、タップした。正しい数字まで。そしてそれは、たいてい、彼のトレイナーと群衆がブロークアウトしたときだった。チアーズの中で」
第8文。
Then he would stop.
「そのとき、彼はやめた」
第9文。
When he couldn't see or hear the audience or his trainer, (B).
「彼は見ることや聞くことができなかったとき、聴衆やトレイナーを。」
第10文。
There's a lot that computer science can learn from Hans today.
「多くのことがある。コンピュータ・サイエンスが学ぶことができる。ハンスから。今日」
第11文。
An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information.
「加速する研究分野は言う。大部分のAI、私たちがこれまでのところ作った、は、十分に学んだ。正しい答を与えられるように。しかし、本当には、情報を理解することなしに」
「すばらしい」
第12文。
Consequently, most types of artificial intelligence are relatively easy to deceive.
「コンシーケントリーに、大部分のタイプのAIは、比較的簡単だ。デシーブするのが」
「deceive、わかりませんか」
「わかりません」
「うーん、それは残念」
さて、問1から見てみましょう。
まずは、該当箇所と、そして問1を見直しましょう。
He would ask his horse, Clever Hans, to solve simple mathematical equation.
「彼は彼の馬、クレバー・ハンスに尋ねた。単純なマスマティカルなイクエーションを解くことを」
In response, Hans would tap his hoof for the correct answer. (A).
「返事の中で、ハンスは彼のひづめをタップした。正しい答のために」
問1 空所(A)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. If asked how many digits are in "4321," four taps.
b. If asked the time around noon, twelve taps
c. The numeral "9" refer to what number? Nine taps.
d. The result of dividing eight by two? Four taps.
残念ですが、上の日本語訳だけでは、正解に到達できません。
飼い主が、馬に何か解くように尋ねていて、馬が何か答えていることしか読み取れないからです。
そうなると、全ての選択肢が、何か問題の形にはなっていますし、馬が何回かタップしていますから、どれも正しく見えてしまいます。
a. 「4321」は何桁かを尋ねるならば、4回タップ。
b. 12時頃に、時刻を尋ねると、12回タップ。
c. 数字の「9」は、どんな数か?9回タップ。
d. 8を2で割った結果は?4回タップ。
mathematical の意味を知らなかったことが、ここで大きく影響しています。
mathematical は、「数学の」という意味です。
ただし、第1文に書いてあったことをしっかり覚えているのなら、「彼の馬は数学ができる」ということが大ヒントにはなったはずです。
飼い主は、ハンスという馬に、単純な数学の問題を解くよう頼んでいるのです。
ハンスはひづめをタップします。正しい答として。
ということは、空所(A)は、単純な数学の問題の具体例のはずです。
上の中で、単純な数学の問題は?
8÷2=4
という問題を説明している、d が正解です。
a や c も、数学がらみではないのか?
厳密に言えばそうなりますが、他の選択肢は、数学というよりも、言葉の意味を理解していることのほうに重点がおかれてしまいます。
これは、馬を使った見世物の話。
「計算できる馬、ハンス」をわかりやすく見せるならば、d だったはずでしょう。
ただ、
The result of dividing eight by two? Four taps.
という選択肢が、8÷2を意味していることが読み取れないと、d は早い時期に除外されてしまう可能性もあります。
英語で算数の問題をどう書くのかは、中学や高校の英語の授業で学習する内容ではないので、少し高度です。
というわけで、問1は、思いがけず、正答するのが難しい問題でした。
問1くらいは正解したい、という人の出鼻をくじく問題です。
続いて、問2を見てみましょう。
When he couldn't see or hear the audience or his trainer, (B).
問2 空所(B)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. he would feel tapping in his heart
b. he would keep tapping and tapping
c. he would start tapping the audience
d. he would tap out the right answer
ハンスは観客やトレーナーを見たり声を聞いたりできなかったときは、どうなったのか?
その前に、解説がありました。
The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions.
Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers.
ここでも、 mathematical の意味がわかっていれば、それ以外の単語の意味が多少わからなくても文意は取れると思います。
ハンスは、本当は、数学の問題を解いていなかったのです。
人々のリアクションに反応していたのでした。
トレーナーや群衆が喜んで沸き上がったところで、タップするのをやめていただけだったのです。
だから、問2の答は、b です。
When he couldn't see or hear the audience or his trainer, he would keep tapping and tapping.
ハンスは、観客やトレーナーを見たり音を聞いたりできないときは、タップし続けたのでした。
問3 下線部There's a lot that computer science can learn from Hans today. とあるが、Hans の逸話から、computer science が学べることは何か。最も適切なものを次のa~dから1つ選びなさい。
a. 賢いふるまいを見せたとしても、称賛してくれる人々がいないのなら意味がない、ということ。
b. 最初は賢くなくても、きちんと訓練すれば、数の計算を正しくできるようになる、ということ。
c. 正しい答を出しているからといって、問題を正しく理解しているとは限らない、ということ。
d . 人々の期待に迎合しすぎると、元々は解けていた問題さえ、正しく解けなくなる、ということ。
ここが、起死回生のポイントではあります。
選択肢が日本語の問題は、誤答の選択肢でさえヒントになります。
ここまで、全く話が理解できなかった人も、ここで落ち着いて選択肢を読むことで、
「こういう話なのか!」
と理解できる可能性があります。
「賢いふるまい」「賞賛してくれる人」「数の計算」「正しい答」「問題を正しく理解」
など、正解がわかっていて振り返ると、キーワードがちりばめられていることに気づきます。
ただ、これは非常に難しい読解です。
モヤモヤしている人は、こういうヒントを正しく活用できる機会はほとんどないと思います。
むしろ、意味がよく取れたその後の文が参考になるでしょう。
An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information.
「加速する研究分野は言う。大部分のAI、私たちがこれまでのところ作った、は、十分に学んだ。正しい答を与えられるように。しかし、本当には、情報を理解することなしに」
AIは、情報を理解することなしに、正しい答を出している・・・。
ここで、馬のハンスが、理解せずに問題を解いている、というおおよその状況さえ読み取れていれば、では、その逸話から、コンピュータ・サイエンスが学べることを判断することが可能です。
馬は、解いているように見えても、解いてはいない。
そのことから、コンピュータ・サイエンスが学べることは?
正解は、c です。
コンピュータが正解を出していても、それは、問題を正しく理解しているからではないのです。
馬が問題を理解していなかったように、コンピュータも、問題を理解していない。
これは、何とか正解にたどりつける問題です。
とはいえ、この英文、mathematical の意味がわかれば、もっとわかりやすかったのです。
そういう意味で、高校生が覚えておくべき基本英単語は、絶対に覚えてほしいのでもあります。
mathematics という「数学」の正式名称を知らず、math という略称しか覚えていないと、「数学」とこの単語が結びつかず、その派生語をも把握できなくなるようです。
高校生が覚えておくべき基本英単語とは、学校が、英語の授業で配布し、毎週のようにそこから単語テストをしてくれている単語集の単語です。
そういうものを迷惑がって活用せず、単語テストのときだけちょろちょろっと覚えて、すぐに忘れ、単語集が定期テストの範囲のときは、捨てる。
その繰り返しで、高3になっても中学英語しかわからない子に、何人も出会ってきました。
「覚えようとしているけれど、覚えられないんです」
という言い訳も、繰り返し聞いてきました。
でも、必要な単語が身についている英語秀才がやっていることを、彼らはやっていませんでした。
その当たり前のことに気づいてほしいのです。
英語学習には、時間が必要です。
惜しみなく、単語暗記に時間を注ぐ必要があります。
「覚えてもどうせ忘れるから、時間がもったいない」
「他にやることがあるのに、英語にそんなに時間はかけられない」
そんな言い訳をしながら、スマホばかり見ている。
スマホには、惜しみなく時間を注いでいる。
その生活を変えてください。
英単語は、たいていの人は、上手く覚えられません。
覚えようとして覚えられず、忘れて、また覚えて、の繰り返しです。
つらいし、自分の頭の悪さにうんざりするし、泣きたくなるし。
その繰り返しです。
しかし、その先、気がつくと、以前よりは英単語がわかっているのです。
いつの間にか、英文が読めるようになっています。
ただし、それには、年単位の時間がかかります。
今日から、単語暗記を。
英文が読めないのは、結局、基本単語を覚えていないことが最大の要因です。
In the early 1900's, Wilhelm von Osten, a German horse trainer and mathematician, told the world that his horse could do math. For years, von Osten traveled Germany giving demonstrations of this phenomenon. He would ask his horse, Clever Hans, to solve simple mathematical equation. In response, Hans would tap his hoof for the correct answer. (A).
Broad public interest in Clever Hans persuaded the German Board of Education to establish a commission to investigate the validity of von Oster's claims about his horse's abilities. The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions. Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers. Then he would stop. When he couldn't see or hear the audience or his trainer, (B).
There's a lot that computer science can learn from Hans today. An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information. Consequently, most types of artificial intelligence are relatively easy to deceive.
問1 空所(A)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. If asked how many digits are in "4321," four taps.
b. If asked the time around noon, twelve taps
c. The numeral "9" refer to what number? Nine taps.
d. The result of dividing eight by two? Four taps.
問2 空所(B)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. he would feel tapping in his heart
b. he would keep tapping and tapping
c. he would start tapping the audience
d. he would tap out the right answer
問3 下線部There's a lot that computer science can learn from Hans today. とあるが、Hans の逸話から、computer science が学べることとは何か。最も適切なものを次のa~dから1つ選びなさい。
a. 賢いふるまいを見せたとしても、称賛してくれる人々がいないのなら意味がない、ということ。
b. 最初は賢くなくても、きちんと訓練すれば、数の計算を正しくできるようになる、ということ。
c. 正しい答を出しているからといって、問題を正しく理解しているとは限らない、ということ。
d . 人々の期待に迎合しすぎると、元々は解けていた問題さえ、正しく解けなくなる、ということ。
今回も、第1文から、わからない単語はわからないまま、生徒に訳してもらったときのこと。
しかし、これが出来るのは、コミュニケーションが取れる子だということも強調したいことです。
わからない英語は英語のままで訳してと幾度促しても、わからない単語が1語あるだけで黙り込んでしまう子もまた多いのです。
それでは英語を読む練習にならないと説得しても、恥ずかしいのか、本人の中で納得できない部分があるのか、黙り込み、私の助けを待ってしまいます。
私が逐語訳をしてあげなければ結局先に進まないので、わからない単語がある中で英文を読んでいく練習になりません。
また、何度説明しても、前から順番に訳さず、日本語らしい順番にしようとして混乱し、その結果黙り込む、という子も多いです。
仕方なく私が訳すと、何だか色々とメモを取ります。
わからなかった単語の意味を書き込んでいるのですが、そんなもの、英文を読み進めていく力にはつながりません。
メモを取っただけで満足してしまう場合が多いのです。
その単語は次回はマスターしている、ということはあまり期待できません。
メモを取ることで勉強した気になってしまうのだと思うのですが、メモを取ることは、勉強ではないのです。
頭に入れることが、勉強です。
真面目なのだけれど勉強が下手な子は、そのように、何か勉強した跡を残したがります。
頭を使わない方向の勉強をしがちです。
単語の意味が知りたかったら、後で、単語集で意味を調べなさい、と繰り返し助言し、何とか自力で読み進めていける方向に指導しています。
単語の意味がわからなくて悔しいのなら、単語暗記をもっと本気でやったらいい。
それと並行して、わからない単語は、わからないまま、読み進める練習も必要。
繰り返しその話をし、わからない単語が1つあるとそこで押し黙ってしまう子も、自力で読み進めていけるよう指導しています。
そんなわけで、第1文。
In the early 1900's, Wilhelm von Osten, a German horse trainer and mathematician, told the world that his horse could do math.
「1900年代初め、ウィルヘルム・バン・オーステン、ドイツの馬のトレイナーでマスマティシャンは、世界に話した。彼の馬は数学ができると」
「・・・はい。mathematician って何でしょうね」
「・・・」
第2文。
For years, von Osten traveled Germany giving demonstrations of this phenomenon.
「何年もの間、バン・オースティンは旅行した。ドイツを。デモンストレーションを与えながら。このポネオネノンを」
「フェノメナンです」
第3文。
He would ask his horse, Clever Hans, to solve simple mathematical equation.
「彼は彼の馬、クレバー・ハンスに尋ねた。単純なマスマティカルなイクエーションを解くことを」
「mathematical って、何ですかね」
「・・・」
第4文。
In response, Hans would tap his hoof for the correct answer. (A).
「返事で、ハンスは彼のひづめをタップした。正しい答のために」
「いいですね」
ひづめは、欄外に、注釈が載っていました。
第5文。
Broad public interest in Clever Hans persuaded the German Board of Education to establish a commission to investigate the validity of von Oster's claims about his horse's abilities.
「ブロードなパブリックの興味、クレバー・ハンスの、は、パースェードした。ジャーマン・ボード・オブ・エデュケーションを。コミッションを設立するように。調べるために。バン・オースティンの主張を。彼の馬についての」
「おお。頑張った!」
第6文。
The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions.
「コミッションは、発見した。クレバー・ハンスは本当は解いていなかった。マスマティカルなイクエーションを。全く。しかし、反応していた。人々のリアクションに」
「うん」
第7文。
Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers.
「ハンスは、タップした。正しい数字まで。そしてそれは、たいてい、彼のトレイナーと群衆がブロークアウトしたときだった。チアーズの中で」
第8文。
Then he would stop.
「そのとき、彼はやめた」
第9文。
When he couldn't see or hear the audience or his trainer, (B).
「彼は見ることや聞くことができなかったとき、聴衆やトレイナーを。」
第10文。
There's a lot that computer science can learn from Hans today.
「多くのことがある。コンピュータ・サイエンスが学ぶことができる。ハンスから。今日」
第11文。
An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information.
「加速する研究分野は言う。大部分のAI、私たちがこれまでのところ作った、は、十分に学んだ。正しい答を与えられるように。しかし、本当には、情報を理解することなしに」
「すばらしい」
第12文。
Consequently, most types of artificial intelligence are relatively easy to deceive.
「コンシーケントリーに、大部分のタイプのAIは、比較的簡単だ。デシーブするのが」
「deceive、わかりませんか」
「わかりません」
「うーん、それは残念」
さて、問1から見てみましょう。
まずは、該当箇所と、そして問1を見直しましょう。
He would ask his horse, Clever Hans, to solve simple mathematical equation.
「彼は彼の馬、クレバー・ハンスに尋ねた。単純なマスマティカルなイクエーションを解くことを」
In response, Hans would tap his hoof for the correct answer. (A).
「返事の中で、ハンスは彼のひづめをタップした。正しい答のために」
問1 空所(A)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. If asked how many digits are in "4321," four taps.
b. If asked the time around noon, twelve taps
c. The numeral "9" refer to what number? Nine taps.
d. The result of dividing eight by two? Four taps.
残念ですが、上の日本語訳だけでは、正解に到達できません。
飼い主が、馬に何か解くように尋ねていて、馬が何か答えていることしか読み取れないからです。
そうなると、全ての選択肢が、何か問題の形にはなっていますし、馬が何回かタップしていますから、どれも正しく見えてしまいます。
a. 「4321」は何桁かを尋ねるならば、4回タップ。
b. 12時頃に、時刻を尋ねると、12回タップ。
c. 数字の「9」は、どんな数か?9回タップ。
d. 8を2で割った結果は?4回タップ。
mathematical の意味を知らなかったことが、ここで大きく影響しています。
mathematical は、「数学の」という意味です。
ただし、第1文に書いてあったことをしっかり覚えているのなら、「彼の馬は数学ができる」ということが大ヒントにはなったはずです。
飼い主は、ハンスという馬に、単純な数学の問題を解くよう頼んでいるのです。
ハンスはひづめをタップします。正しい答として。
ということは、空所(A)は、単純な数学の問題の具体例のはずです。
上の中で、単純な数学の問題は?
8÷2=4
という問題を説明している、d が正解です。
a や c も、数学がらみではないのか?
厳密に言えばそうなりますが、他の選択肢は、数学というよりも、言葉の意味を理解していることのほうに重点がおかれてしまいます。
これは、馬を使った見世物の話。
「計算できる馬、ハンス」をわかりやすく見せるならば、d だったはずでしょう。
ただ、
The result of dividing eight by two? Four taps.
という選択肢が、8÷2を意味していることが読み取れないと、d は早い時期に除外されてしまう可能性もあります。
英語で算数の問題をどう書くのかは、中学や高校の英語の授業で学習する内容ではないので、少し高度です。
というわけで、問1は、思いがけず、正答するのが難しい問題でした。
問1くらいは正解したい、という人の出鼻をくじく問題です。
続いて、問2を見てみましょう。
When he couldn't see or hear the audience or his trainer, (B).
問2 空所(B)に入る最も適切なものを、次のa~dから1つ選びなさい。
a. he would feel tapping in his heart
b. he would keep tapping and tapping
c. he would start tapping the audience
d. he would tap out the right answer
ハンスは観客やトレーナーを見たり声を聞いたりできなかったときは、どうなったのか?
その前に、解説がありました。
The commission found that Clever Hans wasn't really solving mathematical equations at all, but responding to people's reactions.
Hans would tap up until the correct number, which was usually when his trainer and the crowd broke out in cheers.
ここでも、 mathematical の意味がわかっていれば、それ以外の単語の意味が多少わからなくても文意は取れると思います。
ハンスは、本当は、数学の問題を解いていなかったのです。
人々のリアクションに反応していたのでした。
トレーナーや群衆が喜んで沸き上がったところで、タップするのをやめていただけだったのです。
だから、問2の答は、b です。
When he couldn't see or hear the audience or his trainer, he would keep tapping and tapping.
ハンスは、観客やトレーナーを見たり音を聞いたりできないときは、タップし続けたのでした。
問3 下線部There's a lot that computer science can learn from Hans today. とあるが、Hans の逸話から、computer science が学べることは何か。最も適切なものを次のa~dから1つ選びなさい。
a. 賢いふるまいを見せたとしても、称賛してくれる人々がいないのなら意味がない、ということ。
b. 最初は賢くなくても、きちんと訓練すれば、数の計算を正しくできるようになる、ということ。
c. 正しい答を出しているからといって、問題を正しく理解しているとは限らない、ということ。
d . 人々の期待に迎合しすぎると、元々は解けていた問題さえ、正しく解けなくなる、ということ。
ここが、起死回生のポイントではあります。
選択肢が日本語の問題は、誤答の選択肢でさえヒントになります。
ここまで、全く話が理解できなかった人も、ここで落ち着いて選択肢を読むことで、
「こういう話なのか!」
と理解できる可能性があります。
「賢いふるまい」「賞賛してくれる人」「数の計算」「正しい答」「問題を正しく理解」
など、正解がわかっていて振り返ると、キーワードがちりばめられていることに気づきます。
ただ、これは非常に難しい読解です。
モヤモヤしている人は、こういうヒントを正しく活用できる機会はほとんどないと思います。
むしろ、意味がよく取れたその後の文が参考になるでしょう。
An accelerating field of research tells that most of the artificial intelligence (AI) we've created so far has learned enough to give a correct answer, but without truly understanding the information.
「加速する研究分野は言う。大部分のAI、私たちがこれまでのところ作った、は、十分に学んだ。正しい答を与えられるように。しかし、本当には、情報を理解することなしに」
AIは、情報を理解することなしに、正しい答を出している・・・。
ここで、馬のハンスが、理解せずに問題を解いている、というおおよその状況さえ読み取れていれば、では、その逸話から、コンピュータ・サイエンスが学べることを判断することが可能です。
馬は、解いているように見えても、解いてはいない。
そのことから、コンピュータ・サイエンスが学べることは?
正解は、c です。
コンピュータが正解を出していても、それは、問題を正しく理解しているからではないのです。
馬が問題を理解していなかったように、コンピュータも、問題を理解していない。
これは、何とか正解にたどりつける問題です。
とはいえ、この英文、mathematical の意味がわかれば、もっとわかりやすかったのです。
そういう意味で、高校生が覚えておくべき基本英単語は、絶対に覚えてほしいのでもあります。
mathematics という「数学」の正式名称を知らず、math という略称しか覚えていないと、「数学」とこの単語が結びつかず、その派生語をも把握できなくなるようです。
高校生が覚えておくべき基本英単語とは、学校が、英語の授業で配布し、毎週のようにそこから単語テストをしてくれている単語集の単語です。
そういうものを迷惑がって活用せず、単語テストのときだけちょろちょろっと覚えて、すぐに忘れ、単語集が定期テストの範囲のときは、捨てる。
その繰り返しで、高3になっても中学英語しかわからない子に、何人も出会ってきました。
「覚えようとしているけれど、覚えられないんです」
という言い訳も、繰り返し聞いてきました。
でも、必要な単語が身についている英語秀才がやっていることを、彼らはやっていませんでした。
その当たり前のことに気づいてほしいのです。
英語学習には、時間が必要です。
惜しみなく、単語暗記に時間を注ぐ必要があります。
「覚えてもどうせ忘れるから、時間がもったいない」
「他にやることがあるのに、英語にそんなに時間はかけられない」
そんな言い訳をしながら、スマホばかり見ている。
スマホには、惜しみなく時間を注いでいる。
その生活を変えてください。
英単語は、たいていの人は、上手く覚えられません。
覚えようとして覚えられず、忘れて、また覚えて、の繰り返しです。
つらいし、自分の頭の悪さにうんざりするし、泣きたくなるし。
その繰り返しです。
しかし、その先、気がつくと、以前よりは英単語がわかっているのです。
いつの間にか、英文が読めるようになっています。
ただし、それには、年単位の時間がかかります。
今日から、単語暗記を。
英文が読めないのは、結局、基本単語を覚えていないことが最大の要因です。
2025年01月12日
小学校算数。立体の表面積。

問題 上の立体の表面積を求めなさい。
小学校の算数の問題でもありますが、中1の数学でも出題される問題です。
この問題の解き方で、その子の算数・数学の習熟度がある程度はわかります。
勿論、1問だけで何もかもがわかるわけではありませんが。
まずは、算数・数学があまり得意ではない子のやりがちな解き方から。
12×18=216
12×17=207
12×12=144
12×8=96
12×6=72
12×9=108
216+207+144+96+72+108=840
18×17=306
6×8=48
306-48=258
258×2=516
840+516=1356
答 1356㎠
うーん・・・。
正解が出ているのだから、構わないと言えば構わないのですが、この解き方で、正解が出る可能性はかなり低いのです。
これらのかけ算、そしてたし算。
そのどこかで、1回でも計算ミスをしたら、正解できないからです。
そして、立体の体積の問題はまあまあ正解できるのに、表面積になるとほとんど正答できない子の多くが、この解き方です。
これは、1面ずつの面積を丁寧に求めていく解き方です。
まずは、側面の1面ずつの面積を求め、たしています。
その後、底面積を求めています。
そして、最後にたしています。
多くの小学生が、この解き方をしてしまいます。
中学受験をしない小学生なら、まあ、これで仕方ないかとも思うのですが、中学生になっても、このままのことがあります。
また、この解き方をする子は、上のように冷静に規則的に一面ずつ立式していくことはできないことが多く、目についた面から立式し、その結果、求めていない面が出たり、同じ面を2回計算したりしてしまうのです。
計算力にも課題があり、結果、このタイプの問題を正解したことは一度もない、ということもしばしばです。
それでも、この解き方しかわからないのならば、仕方ない。
でも、できれば、改めてほしい解き方です。
ただ、こんなふうにチマチマと1本ずつ式を立てて解くのではなく、1本の式にまとめて、計算の工夫をすることが身についているのなら、正答率は上がります。
側面積は、
12×18+12×17+12×12+12×8+12×6+12×9
=12×(18+17+12+8+6+9)
=12×70
=840
底面積は、
18×17-6×8
=306-48
=258
よって、
258×2+840
=56+840
=1356
答 1356㎠
この解き方なら、計算はかなり楽になります。
ただ、一番上のような考え方でこの問題を解く子が、このように1本の式を立てて計算の工夫をする場合は少ないです。
分配法則の逆を使って、くくる・・・。
この考え方は、一般の小学生は、ほぼ身につかないのです。
教えても、そういう考え方のほうが面倒くさい、と顔をしかめます。
あるいは、そのときは理解した顔をしますが、1週間後には忘れています。
複雑な計算をすることになっても、それで計算ミスのリスクが上がっても、一番上のような解き方しかできない。
そういう子が多いのです。
スマートな解き方は後述しますが、この問題を小学生に教えたときに、不思議な解き方をする子がいました。
18×12×2=432
17×12×2=408
17×18×2=612
432+408+612=1452
答 1452㎠
無論、誤答です。
・・・何だろう、この解き方は・・・?
まだ小学生ですから、自分の考え方を説明する力に乏しく、聴き取りには苦労しました。
それでも、何とか聴き取ったことによると。
上の立体は、縦17㎝、横18㎝、高さ12㎝の直方体から、縦8㎝、横6㎝、高さ12㎝の直方体を取り除いたものです。
その子は、「直方体から直方体を取り除いたとき、表面積は変わらない」と思い込んでいたのでした。
だから、取り除く前の直方体で、表面積を求めていたのです。
直方体には、合同な長方形の面が2面ずつあります。
それごとに、面積を求めていたのです。
奇妙な誤解でした。
ただ、それは、重要な考え方も含まれていました。
一番上の地道な解き方をする子が到達できないものの見方でもあるのです。
「直方体から直方体を取り除いたとき、表面積は変わらない」は誤りです。
しかし、「直方体から直方体を取り除いたとき、側面積は変わらない」は事実です。
取り除いたために生まれたへこみの部分の面積は、取り除く前に突出していた部分と等しいからです。
それは、この立体と同じ水平面からの視点でこの立体を見たときに、真正面から見える長方形は、取り除く前に見える真正面の長方形と同じであることからもイメージできると思います。
これは、受験算数としても重要な考え方で、積み木を積み上げる問題等で活用できます。
また、円柱の上に、ひとまわり小さい円柱が載っている立体の表面積を求める際などにも、真上から見て、底面を1つの円として一気に計算するなど、応用範囲の広い考え方でもあります。
ただ、その生徒は、自分のその考え方を、側面積だけに限定せず、底面積も含めてしまったのでした。
直方体から直方体を取り除いた形の立体の場合、側面積は変わりません。
しかし、底面積は、明らかに、えぐれて減ってしまいます。
すぐれた考え方ができる一方で、まだ幼く、混線しやすかったのだと思います。
底面積は減ることを解説しても、上手く理解できない様子で混乱していました。
さて、それでは、よりスマートな解き方は、どんな解き方でしょうか?
スマート、といっても、中学数学になれば、普通に教科書にも参考書にも載っていて、当たり前にこの解き方で解きなさいよ、と推奨される解き方です。
立体の表面積は、展開図をイメージして解きます。
この立体は、底面が複雑な形をしていますが、一種の柱体です。
展開図としては、上下2つの底面と、ひと続きの側面としてとらえるのが一番楽です。
ひと続きの側面は、横に長い長方形です。
その長方形の縦の長さは、立体の高さにあたる12㎝。
横の長さは、底面の周と等しくなります。
そこで、上に書いた誤答の一部分が活用できます。
直方体から直方体を取り除いても、底面の周の長さは変わりません。
したがって、底面の周の長さは、縦17㎝、横18㎝の長方形の周の長さと等しくなります。
よって、側面の横の長さは、
17×2+18×2
=(17+18)×2
=35×2
=70
実際には、こんな途中式は不要で、1行目をしっかり書いた次は、すぐに=70として構いません。
暗算で処理できるレベルの計算となり、それだけ計算ミスの可能性は低くなります。
側面は、縦12㎝、横70㎝の長方形。
これも、暗算できるレベルの計算です。
12×70=840
あとは、底面積。
これは、一番上の解き方と同じです。
底面積は、
18×17-6×8
=306-48
=258
よって、求める表面積は、
840+258×2
=840+516
=1356
答 1356㎠
一番複雑な筆算で、18×17。
あとは、暗算も可能ですが、丁寧に筆算するもよし。
全体に計算が楽になるため、正答率が上がります。
そして、特に私立の入試問題は、そのような企みが隠されている場合が多いのです。
一番上のような地道な計算しかできない子は、時間もかかり、計算ミスにより誤答のリスクも高まります。
一方、スマートな解き方を発想できる子は、短時間で立式し、計算ミスのリスクも少なく正答に至るような数字に、あらかじめ設定されているのです。
当然ですが、一番下のスマートな解法を身に着けてくれる子に教えているときが、一番楽です。
実際は、一番上のような解き方をしてしまう子のほうが圧倒的に多く、教えても教えても、その解き方の呪縛から逃れられない子が大多数で、てのひらから砂がこぼれ落ちるような感覚を味わうのですが。
ところで、これには後日談があります。
真ん中あたりで書いた、奇妙な誤答をした生徒。
面白い視点を持っている子でした。
でも、説明する力が弱い。
このブログのかなり古い記述をたどれば、その子はときどき登場します。
小学校から公立中学に進学し、引き続き、うちの塾で学習を続けました。
中1の数学の定期テストでは、「割合」に関する問題として出題された方程式の文章題で誤答し、クラスメートに、
「式がそもそも間違っている」
と、指摘されてしょげていたりもしました。
しかし、答案を見ると、その子は、「割合」の文章題を、比例式で解いていました。
正しい比例式でした。
割合の考え方で一旦もとにする量を求めてから、ごちゃごちゃと方程式を立てて解くよりも、ずっとスマートな解法でした。
普通の中1は、比例式の形の方程式など立てません。
比例式とは、a : b=c : d という形の式です。
立てた後、どうやってその式を変形すればいいのか、覚えていない中学生も多いです。
自分が手に負えるものではない式など、普通は立てません。
その子は、比例式の変形方法も身につけていましたが、変形の直後に、本当にくだらない計算ミスをして、その問題は0点となっていました。
部分点をもらえる形式のテストではなかったからです。
この子の中には才能が眠っている。
しかし、言葉で説明する力が乏しく、論理的な思考より、ひらめきの力のほうが強いようにも感じる・・・。
集団の中では、侮られやすい子でもありました。
頭の良い子に見えなかったのだと思います。
しかし、後に、その子は、都立自校作成校に合格しました。
都立高校の中でトップクラスの、一般入試とは別の独自入試問題を使用する高校です。
小学校の算数の問題でもありますが、中1の数学でも出題される問題です。
この問題の解き方で、その子の算数・数学の習熟度がある程度はわかります。
勿論、1問だけで何もかもがわかるわけではありませんが。
まずは、算数・数学があまり得意ではない子のやりがちな解き方から。
12×18=216
12×17=207
12×12=144
12×8=96
12×6=72
12×9=108
216+207+144+96+72+108=840
18×17=306
6×8=48
306-48=258
258×2=516
840+516=1356
答 1356㎠
うーん・・・。
正解が出ているのだから、構わないと言えば構わないのですが、この解き方で、正解が出る可能性はかなり低いのです。
これらのかけ算、そしてたし算。
そのどこかで、1回でも計算ミスをしたら、正解できないからです。
そして、立体の体積の問題はまあまあ正解できるのに、表面積になるとほとんど正答できない子の多くが、この解き方です。
これは、1面ずつの面積を丁寧に求めていく解き方です。
まずは、側面の1面ずつの面積を求め、たしています。
その後、底面積を求めています。
そして、最後にたしています。
多くの小学生が、この解き方をしてしまいます。
中学受験をしない小学生なら、まあ、これで仕方ないかとも思うのですが、中学生になっても、このままのことがあります。
また、この解き方をする子は、上のように冷静に規則的に一面ずつ立式していくことはできないことが多く、目についた面から立式し、その結果、求めていない面が出たり、同じ面を2回計算したりしてしまうのです。
計算力にも課題があり、結果、このタイプの問題を正解したことは一度もない、ということもしばしばです。
それでも、この解き方しかわからないのならば、仕方ない。
でも、できれば、改めてほしい解き方です。
ただ、こんなふうにチマチマと1本ずつ式を立てて解くのではなく、1本の式にまとめて、計算の工夫をすることが身についているのなら、正答率は上がります。
側面積は、
12×18+12×17+12×12+12×8+12×6+12×9
=12×(18+17+12+8+6+9)
=12×70
=840
底面積は、
18×17-6×8
=306-48
=258
よって、
258×2+840
=56+840
=1356
答 1356㎠
この解き方なら、計算はかなり楽になります。
ただ、一番上のような考え方でこの問題を解く子が、このように1本の式を立てて計算の工夫をする場合は少ないです。
分配法則の逆を使って、くくる・・・。
この考え方は、一般の小学生は、ほぼ身につかないのです。
教えても、そういう考え方のほうが面倒くさい、と顔をしかめます。
あるいは、そのときは理解した顔をしますが、1週間後には忘れています。
複雑な計算をすることになっても、それで計算ミスのリスクが上がっても、一番上のような解き方しかできない。
そういう子が多いのです。
スマートな解き方は後述しますが、この問題を小学生に教えたときに、不思議な解き方をする子がいました。
18×12×2=432
17×12×2=408
17×18×2=612
432+408+612=1452
答 1452㎠
無論、誤答です。
・・・何だろう、この解き方は・・・?
まだ小学生ですから、自分の考え方を説明する力に乏しく、聴き取りには苦労しました。
それでも、何とか聴き取ったことによると。
上の立体は、縦17㎝、横18㎝、高さ12㎝の直方体から、縦8㎝、横6㎝、高さ12㎝の直方体を取り除いたものです。
その子は、「直方体から直方体を取り除いたとき、表面積は変わらない」と思い込んでいたのでした。
だから、取り除く前の直方体で、表面積を求めていたのです。
直方体には、合同な長方形の面が2面ずつあります。
それごとに、面積を求めていたのです。
奇妙な誤解でした。
ただ、それは、重要な考え方も含まれていました。
一番上の地道な解き方をする子が到達できないものの見方でもあるのです。
「直方体から直方体を取り除いたとき、表面積は変わらない」は誤りです。
しかし、「直方体から直方体を取り除いたとき、側面積は変わらない」は事実です。
取り除いたために生まれたへこみの部分の面積は、取り除く前に突出していた部分と等しいからです。
それは、この立体と同じ水平面からの視点でこの立体を見たときに、真正面から見える長方形は、取り除く前に見える真正面の長方形と同じであることからもイメージできると思います。
これは、受験算数としても重要な考え方で、積み木を積み上げる問題等で活用できます。
また、円柱の上に、ひとまわり小さい円柱が載っている立体の表面積を求める際などにも、真上から見て、底面を1つの円として一気に計算するなど、応用範囲の広い考え方でもあります。
ただ、その生徒は、自分のその考え方を、側面積だけに限定せず、底面積も含めてしまったのでした。
直方体から直方体を取り除いた形の立体の場合、側面積は変わりません。
しかし、底面積は、明らかに、えぐれて減ってしまいます。
すぐれた考え方ができる一方で、まだ幼く、混線しやすかったのだと思います。
底面積は減ることを解説しても、上手く理解できない様子で混乱していました。
さて、それでは、よりスマートな解き方は、どんな解き方でしょうか?
スマート、といっても、中学数学になれば、普通に教科書にも参考書にも載っていて、当たり前にこの解き方で解きなさいよ、と推奨される解き方です。
立体の表面積は、展開図をイメージして解きます。
この立体は、底面が複雑な形をしていますが、一種の柱体です。
展開図としては、上下2つの底面と、ひと続きの側面としてとらえるのが一番楽です。
ひと続きの側面は、横に長い長方形です。
その長方形の縦の長さは、立体の高さにあたる12㎝。
横の長さは、底面の周と等しくなります。
そこで、上に書いた誤答の一部分が活用できます。
直方体から直方体を取り除いても、底面の周の長さは変わりません。
したがって、底面の周の長さは、縦17㎝、横18㎝の長方形の周の長さと等しくなります。
よって、側面の横の長さは、
17×2+18×2
=(17+18)×2
=35×2
=70
実際には、こんな途中式は不要で、1行目をしっかり書いた次は、すぐに=70として構いません。
暗算で処理できるレベルの計算となり、それだけ計算ミスの可能性は低くなります。
側面は、縦12㎝、横70㎝の長方形。
これも、暗算できるレベルの計算です。
12×70=840
あとは、底面積。
これは、一番上の解き方と同じです。
底面積は、
18×17-6×8
=306-48
=258
よって、求める表面積は、
840+258×2
=840+516
=1356
答 1356㎠
一番複雑な筆算で、18×17。
あとは、暗算も可能ですが、丁寧に筆算するもよし。
全体に計算が楽になるため、正答率が上がります。
そして、特に私立の入試問題は、そのような企みが隠されている場合が多いのです。
一番上のような地道な計算しかできない子は、時間もかかり、計算ミスにより誤答のリスクも高まります。
一方、スマートな解き方を発想できる子は、短時間で立式し、計算ミスのリスクも少なく正答に至るような数字に、あらかじめ設定されているのです。
当然ですが、一番下のスマートな解法を身に着けてくれる子に教えているときが、一番楽です。
実際は、一番上のような解き方をしてしまう子のほうが圧倒的に多く、教えても教えても、その解き方の呪縛から逃れられない子が大多数で、てのひらから砂がこぼれ落ちるような感覚を味わうのですが。
ところで、これには後日談があります。
真ん中あたりで書いた、奇妙な誤答をした生徒。
面白い視点を持っている子でした。
でも、説明する力が弱い。
このブログのかなり古い記述をたどれば、その子はときどき登場します。
小学校から公立中学に進学し、引き続き、うちの塾で学習を続けました。
中1の数学の定期テストでは、「割合」に関する問題として出題された方程式の文章題で誤答し、クラスメートに、
「式がそもそも間違っている」
と、指摘されてしょげていたりもしました。
しかし、答案を見ると、その子は、「割合」の文章題を、比例式で解いていました。
正しい比例式でした。
割合の考え方で一旦もとにする量を求めてから、ごちゃごちゃと方程式を立てて解くよりも、ずっとスマートな解法でした。
普通の中1は、比例式の形の方程式など立てません。
比例式とは、a : b=c : d という形の式です。
立てた後、どうやってその式を変形すればいいのか、覚えていない中学生も多いです。
自分が手に負えるものではない式など、普通は立てません。
その子は、比例式の変形方法も身につけていましたが、変形の直後に、本当にくだらない計算ミスをして、その問題は0点となっていました。
部分点をもらえる形式のテストではなかったからです。
この子の中には才能が眠っている。
しかし、言葉で説明する力が乏しく、論理的な思考より、ひらめきの力のほうが強いようにも感じる・・・。
集団の中では、侮られやすい子でもありました。
頭の良い子に見えなかったのだと思います。
しかし、後に、その子は、都立自校作成校に合格しました。
都立高校の中でトップクラスの、一般入試とは別の独自入試問題を使用する高校です。
2025年01月06日
どうすれば、テストの得点が上がるのか。

どうすればテストの得点を上げていくことができるでしょうか。
どうすれば、成績は上がるのか。
評判の良い塾に通えば、夢のように成績は上がるのか?
評判の良い授業動画を見れば、たちまち成績は上がるのか?
何にでも即効性を求める風潮があります。
また、誰でも必ず成績は上がり、東大にも合格できるといった風評のようなものがネットを中心に蔓延しています。
そのせいか、テストの点数を上げることを簡単なことのように思う保護者の方もいるかもしれませんが、実際はそんなに簡単なことではありません。
成績が上がるまでには、時間が必要です。
年単位の時間がかかることも珍しくありません。
本人が抱えている学習上の課題を1つ1つ解決していかなければならないからです。
そのため、何が課題であるのか、まずその現実を把握する必要があります。
その現実を、生徒本人に自覚してもらう必要もあります。
保護者の方が考えるよりもはるか手前に課題があり、それが学習に影響している場合が多いのです。
そもそも、生徒にやる気がない。
保護者の方が、
「だったら、やる気を出させてくださいよ」
と思う気持ちが切実なのはよくわかるのですが、それは、簡単なことではありません。
生徒自身の中に、できればやる気を出したい、でも、やる気が出なくて困っているという気持ちがあるのならまだ何とかなるかもしれません。
しかし、子どもは、どんなに幼くても、本人なりに判断をしています。
「勉強は、しない」
という強い判断を本人がしている場合があります。
「今は勉強なんか必要ない。受験前になったら、やる」
と本人が判断している場合、大人による説得はかなり難しいです。
客観的には愚かな判断でも、それは、本人の判断です。
本人の判断は、何よりも本人が一番に尊重します。
心は動きません。
せめてその点はクリアしていて、本人にも何とかしたいという気持ちがある場合でも、課題は山積しています。
かつてうちの塾の生徒で最も困難だったのが、学校で今何を勉強しているのかわからない、という場合でした。
「うちの先生は教科書を使わない。いつもプリントだから、わからない」
というのです。
プリント学習といっても学校の教科書に載っていない特殊なことをやっている場合は少なく、教科書と同じ単元をプリントで演習している場合がほとんどですが、そのことを理解していませんでした。
本人の理解力不足ということもありますが、中学生くらいですと勉強しない理由を無意識に探す傾向もありますから、
「学校の先生が悪いんだ。自分は悪くない」
とするのに好都合で、本人もつきつめて考えてみなかったのかもしれません。
じゃあ私がプリントを見るから塾に持ってきなさいと言っても毎回忘れてきました。
口頭で、学習内容を説明してもらっても、下手をすると大単元の名前さえ言い間違えるほどで、全てが曖昧でした。
保護者に連絡をして、その点から改善していきました。
先を見ることができない子も多いです。
「テスト範囲がまだ出ていないから、テスト勉強はできない」
と言う子もいました。
「でもね、テスト範囲の始まりは、前のテスト範囲の次からでしょう?そして、テスト範囲の終わりは、今やっているところか、その少し先くらいでしょう」
と説明すると、初めてそのことに気がついたという様子で、驚いていました。
そういうことを考えたことがなかったのでしょう。
テスト範囲が正式に発表されるテスト1週間前からしかテスト勉強はできない。
それは学校が悪いので自分の責任ではない。
本気でそう思っていたのです。
あるいはそのように言い訳している場合もあるでしょう。
定期テスト当日に提出するワークや準拠問題集などの課題に関してもそうです。
「学校はテストが近くなってから急に何十ページも宿題を出す。ひどい」
と言う子もいました。
しかし、テストの度にそうなのですから、学校で勉強したことは同じ週のうちに学校のワークを解いておけば、良い家庭学習になります。
まとめのページは残しておいてテスト前にやるとテスト対策になります。
学校の先生は当然そのつもりでそういう課題を出しているでしょう。
勉強のできる子の多くは、そのように学校の課題を活用しています。
なかには塾のハイレベルな課題を解くのに忙しく、学校の課題をテスト直前に丸々残してしまう秀才というのもいますが、あの人たちは、学校の課題は1時間か2時間で解いてしまえるので、真似しているとひどい目にあいます。
私立の中高一貫校は年間の進度とテスト範囲を書面にして配っていることも多いのですが、そうではない場合、次に何を学習するのか生徒は知らない、もちろん私にもわからないということもあります。
教科書の順番通りにやってくれれば良いけれど、そうとは限りません。
代数と幾何を分けていない学校の場合、今までずっと代数をやっていたのに、突然幾何に入ったということもありました。
そういう報告を受けて、
「うん、わかった。じゃあ幾何の問題集を出して」
と言うと、
「あ。持ってきていない・・・」
とその子は答えました。
「え?だって、学校は幾何の勉強に入ったんでしょう?」
「・・・」
英語の教科書を置いてきてしまう子もいました。
公立中学は「置き勉」推奨のこともあります。
しかし、それは普段の家庭学習で使うことはなさそうな重い教科書や資料集の話で、英語の教科書なんて薄いですし、毎日家庭で使うべきものなのに、学校に置いてきてしまうのです。
高校生になってもその習慣は消えませんでした。
「・・・教科書がないのに、どうやって予習をするんですか?」
私がそう問うと、呆然としていました。
宿題に出したテキストしか持ってこない子もいました。
塾は宿題の答えあわせしかしないわけではありません。
学校は今何をやっているのか。
それにあわせて塾の授業は何をやることになるのか。
そのために必要なテキストは何なのか。
それを考えて用意してきなさい。
そういう話をすると耳を塞いでしまう子もいました。
「そういうの、私は一番苦手だから。わからないから」
「・・・・・だったら、全部持ってきなさい。勝手に判断して教材を置いてきたらダメだよ。置いてくるのは、一種の判断でしょう?判断が苦手なら、何も判断しないほうがいい。全部持ってきなさい」
何を持ってきたら良いかの判断はできない。
何を置いてくるかの判断は勝手にしてしまう・・・。
子どもは、判断をしないわけではないのです。
間違った判断をしてしまうだけなのです。
個別指導ですから、生徒の通う学校もバラバラです。
その生徒の情報収集力がそのままテスト対策のクオリティになってしまうのが歯がゆいところです。
例えば、夏休みの課題だった問題集から十数ページがテスト範囲だと発表されます。
10日前くらいに急にそんなことを言われても対策できません。
しかし、それは本当に突然言われたことなのか?
実は前からわかっていたことなのではないか?
それを予測し準備していた子もいたのではないか?
いや、むしろそういう子のほうが多いということもあり得るのではないか?
次のテストも同じ問題集からまた出題されるのではないか?
だとしたら、どこが出るのか本当はもうわかっているのではないか?
そのように問いかけても、その子の表情はぼんやりしています。
本当にわからない様子です。
学校の宿題だけはいつもしっかり持ってくるのに、塾で渡した問題集やプリントは忘れてくる子というのもいました。
これは、かなり意図的な匂いがしました。
他に教材がないので、塾で学校の宿題を解くしかなくなります。
とにかく学校の宿題がわからない。
自力で解けない。
本人はそう言うのですが、そういうのは嘘とは言わないまでも大袈裟な表現である場合がほとんどで、大半は自力で解けるのです。
わからない問題も中にはあるでしょう。
そうした1問2問を質問したいというのはわかるのですが、塾で学校の宿題をやりたい、個別指導はそういうことをしてくれるはずという願望が本人にある場合、学校の宿題だけはしっかり持ってくる、塾のテキストや宿題は置いてくるということがしばらく続きました。
しかし、学校の宿題を塾でやったら、家では何をやるのでしょう。
おそらく何もしないでしょう。
私が教えながら解いたらスラスラと進むので、1週間の家庭学習は塾で学校の宿題を解いた90分だけ。
そんなことになってしまいます。
こういう形をとると、学校の宿題は今までになくスムーズにこなせるものですから、本人も、そして場合によっては保護者の方も、勘違いをしてしまうことがあります。
ああ、塾に行くと何もかも上手くいく。
これは、テストの点数も上がるはず。
・・・・・・上がるわけがないんです。
こんな勉強をしていたら、むしろ、確実に下がります。
そのように説明するのですが、それでも「学校の宿題がー」「宿題がー」と言い続ける場合は、実際にテストの結果が出るのを待つしかありません。
テストで悪い結果が出て、何が問題であるか向き合う気持ちになってくれたら、それからが本当の始まりです。
学校の宿題を自分で解けるように。
それが目標であるなら、地力をつけなければなりません。
そのためには、これまでの学習量の不足を改めなければなりません。
以前に未消化だった内容のせいで今の勉強がわからないのなら、そこに戻って復習しなればなりません。
しかし、本人にとっては塾の宿題も上手くこなせず、学校の宿題と塾の宿題と、結局宿題が2倍になって苦しいばかりとなります。
塾の宿題の答え合わせをしても、最初のうちは不正解や解いていない問題があまりにも多く、90分かけても宿題の解き直しが終わりません。
その間にも学校の授業は先に進み、わからないことはたまっていきます。
毎回、塾の宿題が負担だ。
しかも、学校の宿題を解くのに何の助けにもならない。
苦しい時期が続きます。
錆びた大型機械が動き出すには、まず動きだすために多くのエネルギーが必要です。
錆びていた時期が長いほど、動きだすための時間も長く必要となります。
とにかく、動くようにすること。
自力で走行できるようにすること。
自分で学習できるようにすること。
そのための苦しさに耐えることができるかどうか。
それが最初の課題です。
こうした課題の解決に、年単位の時間のかかる子もいますが、通塾期間が長くなるにつれて、徐々に解決していきます。
そうは言っても、高校生の場合、英語は、単語集や熟語集のテスト範囲を平気で捨てるので、その分の-20点は最初から確定していたり。
公立中学の生徒の場合、数学は、見たことのない「活用」の文章題が何問も出ていたり。
1つのことが解決すれば、また次の課題が見えてきます。
そんな中でも、焦らず、一歩ずつ前に進んでいきましょう。
うちの塾に中2から通っているある生徒は、その当時、father と family の見分けがつきませんでした。
「ああ・・・、似てますね。・・・って、fa だけじゃないの!」
と、突っ込む繰り返しでした。
英語に対する識字の感覚が驚くほど雑な子は、たまにいます。
英文字は26文字しかないので、雑に言えばどんな単語も他の何かと似ています。
その区別がつかなかったのでした。
能力的な問題の場合もありますが、本人の意識が低いだけの場合なら、改善可能です。
今、その子は、志望大学の過去問を、まがりなりにも自力で読んでいます。
何という成長だろう、と感じます。
即効性を期待するから、挫折感もすぐにやってきます。
前よりも良くなっていることが、必ずあるはずです。
2024年12月28日
冬休みなので、難問を。円に外接する多角形の1辺の長さ。
冬休みなので、難問を解いてみましょう。
中3または高校数学の知識で解くことができる問題です。
問題1 半径1の円に外接する正六角形の1辺の長さを求めよ。
問題2 半径1の円に外接する正十二角形の1辺の長さを求めよ。
自分で解きたい方は、ここでブログを閉じてください。
以下は、解説です。
まずは問題1から。
こういう問題では、図を自分で描く必要がありますが、幾度それを助言されても、絶対に図を描かない生徒もいます。
描き方がわからない、と本人たちは言うのですが、その「わからない」の何がわからないのかは、不可解です。
円を描いて、その周りに、下手でもいいから正六角形を描くことの何がわからないのか?
上手く描ける気がしないし、描いたからといって、それで解ける気がしない。
そういう気持ちのほうが強いのではないかと思うのです。
結局、本人の中で、図を描くことが、自分の気持ちを少し犠牲にしてでも行うべきことだと思えないのではないか。
生徒は、どんなに数学が苦手な子でも、本人なりに何かを判断しています。
その判断が間違っているから、数学が得意にならないのだと思うのです。
一方、数学が好きな人は、
「この問題で図を描かないなんて、それじゃ解けないのに。何でそんな気持ち悪いことができるんだろう。図を描けば、解けるのに」
という確信が強いのです。
というわけで、図を描きましょう。
画像の左側が、半径1の円に外接する正六角形の図です。

円の中心をOとし、正六角形の頂点を図のように、点A、点Bとしてみました。
正六角形ですので、辺の長さはすべて等しいです。
中心Oと正六角形の角頂点を結んでできる三角形は、すべて合同です。
360÷6=60 で、
∠AOB=60° となります。
また、△OABは、OA=OBの二等辺三角形です。
頂角が60°の二等辺三角形。
つまり、△ABCは、正三角形だとわかります。
これでわかりました。
正三角形も一種の二等辺三角形ですから、頂角の二等分線は底辺を垂直に二等分します。
よって、OM⊥AB
また、AM=BM
∠BOM=30°
∠OBM=60°
です。
△OMBは、内角が30°、60°、90° の特別な比の三角形だとわかりました。
辺の比は、1:2:√3
ここで、OMは、円の半径ですから、OM=1
よって、BM=1÷√3=1/√3=√3/3
AB=2BM=2√3 / 3
したがって、外接する正六角形の1辺の長さは、2√3 / 3 です。
続いて、問題2を解きましょう。
問題2 半径1の円に外接する正十二角形の1辺の長さを求めよ。

今度は右側の図を見てください。
半径1の円に外接する正十二角形を、正六角形を用いて描き起こそうとしています。
正十二角形の各頂点と円の中心Oとを結べば、12個の合同な二等辺三角形を描くことができます。
その二等辺三角形の頂角は、
360÷12=30
で、30°
頂角30°の二等辺三角形を1つ描いてみましょう。
OBと円との交点をEとします。
∠MOBの二等分線とMBとの交点をCとします。
∠COE=15°
CEの延長上に、∠EOD=15° となる点Dをとります。
△OCDは、頂角30°の二等辺三角形となります。
二等辺三角形の性質から、OE⊥CDで、CE=DEとなります。
さあ、準備は整いました。
CEの長さがわかれば、それを2倍すれば、正十二角形の1辺の長さです。
CEを1辺に持つ直角三角形があれば・・・。
あります!
△BCEが、直角三角形です。
OEは、円の半径ですから、
OE=1
△OABは正三角形でしたから、問題1より、
OB=2√3 / 3
よって、BE=2√3/3 -1
∠B=60°
∠CEB=90° ですから、
△BCEも、特別な比の直角三角形です!
よって、
CE=√3・BE=√3(2√3/3-1)=2-√3
正十二角形の1辺はCDです。
CD=2CE=2(2-√3)=4-2√3
したがって、正十二角形の1辺の長さは、4-2√3 です。
図を描いたからこそ、この解き方にたどりつくことができました!
図は大切。
「描き方がわからないし」
「どうせ、描いてもわからないから、無駄だし」
という気持ちもわかるのですが、そんなふうにくさらず、諦めないで、描き続けましょう。
描いたからこそ解けた問題に、いつか必ず到達します。
中3または高校数学の知識で解くことができる問題です。
問題1 半径1の円に外接する正六角形の1辺の長さを求めよ。
問題2 半径1の円に外接する正十二角形の1辺の長さを求めよ。
自分で解きたい方は、ここでブログを閉じてください。
以下は、解説です。
まずは問題1から。
こういう問題では、図を自分で描く必要がありますが、幾度それを助言されても、絶対に図を描かない生徒もいます。
描き方がわからない、と本人たちは言うのですが、その「わからない」の何がわからないのかは、不可解です。
円を描いて、その周りに、下手でもいいから正六角形を描くことの何がわからないのか?
上手く描ける気がしないし、描いたからといって、それで解ける気がしない。
そういう気持ちのほうが強いのではないかと思うのです。
結局、本人の中で、図を描くことが、自分の気持ちを少し犠牲にしてでも行うべきことだと思えないのではないか。
生徒は、どんなに数学が苦手な子でも、本人なりに何かを判断しています。
その判断が間違っているから、数学が得意にならないのだと思うのです。
一方、数学が好きな人は、
「この問題で図を描かないなんて、それじゃ解けないのに。何でそんな気持ち悪いことができるんだろう。図を描けば、解けるのに」
という確信が強いのです。
というわけで、図を描きましょう。
画像の左側が、半径1の円に外接する正六角形の図です。

円の中心をOとし、正六角形の頂点を図のように、点A、点Bとしてみました。
正六角形ですので、辺の長さはすべて等しいです。
中心Oと正六角形の角頂点を結んでできる三角形は、すべて合同です。
360÷6=60 で、
∠AOB=60° となります。
また、△OABは、OA=OBの二等辺三角形です。
頂角が60°の二等辺三角形。
つまり、△ABCは、正三角形だとわかります。
これでわかりました。
正三角形も一種の二等辺三角形ですから、頂角の二等分線は底辺を垂直に二等分します。
よって、OM⊥AB
また、AM=BM
∠BOM=30°
∠OBM=60°
です。
△OMBは、内角が30°、60°、90° の特別な比の三角形だとわかりました。
辺の比は、1:2:√3
ここで、OMは、円の半径ですから、OM=1
よって、BM=1÷√3=1/√3=√3/3
AB=2BM=2√3 / 3
したがって、外接する正六角形の1辺の長さは、2√3 / 3 です。
続いて、問題2を解きましょう。
問題2 半径1の円に外接する正十二角形の1辺の長さを求めよ。

今度は右側の図を見てください。
半径1の円に外接する正十二角形を、正六角形を用いて描き起こそうとしています。
正十二角形の各頂点と円の中心Oとを結べば、12個の合同な二等辺三角形を描くことができます。
その二等辺三角形の頂角は、
360÷12=30
で、30°
頂角30°の二等辺三角形を1つ描いてみましょう。
OBと円との交点をEとします。
∠MOBの二等分線とMBとの交点をCとします。
∠COE=15°
CEの延長上に、∠EOD=15° となる点Dをとります。
△OCDは、頂角30°の二等辺三角形となります。
二等辺三角形の性質から、OE⊥CDで、CE=DEとなります。
さあ、準備は整いました。
CEの長さがわかれば、それを2倍すれば、正十二角形の1辺の長さです。
CEを1辺に持つ直角三角形があれば・・・。
あります!
△BCEが、直角三角形です。
OEは、円の半径ですから、
OE=1
△OABは正三角形でしたから、問題1より、
OB=2√3 / 3
よって、BE=2√3/3 -1
∠B=60°
∠CEB=90° ですから、
△BCEも、特別な比の直角三角形です!
よって、
CE=√3・BE=√3(2√3/3-1)=2-√3
正十二角形の1辺はCDです。
CD=2CE=2(2-√3)=4-2√3
したがって、正十二角形の1辺の長さは、4-2√3 です。
図を描いたからこそ、この解き方にたどりつくことができました!
図は大切。
「描き方がわからないし」
「どうせ、描いてもわからないから、無駄だし」
という気持ちもわかるのですが、そんなふうにくさらず、諦めないで、描き続けましょう。
描いたからこそ解けた問題に、いつか必ず到達します。
2024年12月21日
高校英語長文読解。間違っているものを選ぶ四択問題。

さて、こんな長文問題を生徒と解いたときのことです。
Is there a creative writer who hasn't at times wondered what drives thousands of people to spend thousands of hours thinking about and writing made-up stories? At best these stories will be read by thousands of people who have got nothing better to do than read made-up stories! Is there some evolutionary need that has molded our minds to seek stories? Steven Pinker, the author of How the Mind Works, controversially tells that music confers no survival advantage but that fiction can "supply us with a mental catalogue of the fatal difficulties we might face someday and the outcome of strategies we could make use of in them." Perhaps for writers of fiction the truth of this is even greater. But what does this mean for the mind? Does it tell we have special systems in our brains that have evolved for the purpose of creating stories that might some day be useful in our real lives? And why is it that some people are better at making up stories than others, and if they are, are they therefore better prepared for whatever life throws at them?
問 This paragraph asks all of the following questions EXCEPT
あ. Why do people read and write fiction?
い. Dose the brain have a need to create stories?
う. What is the relation between music and fiction?
え. Does writing stories help us deal with real life?
かなり難しいですが、例によって、わからないところはわからないまま、読んでもらいました。
まずは、第1文。
Is there a creative writer who hasn't at times wondered what drives thousands of people to spend thousands of hours thinking about and writing made-up stories?
「創造的な作家はいるだろうか。ときどき不思議に思うことがない。何が運転するのか。何千人の人々に。費やすように。何千時間考えて書くことを。メイドアップな物語を」
「ここのdrive は、運転するという意味ではなさそうですので、ドライブのままで理解しましょう」
続けて、第2文。
At best these stories will be read by thousands of people who have got nothing better to do than read made-up stories!
「せいぜい、これらの物語は、読まれるだろう。何千人の人々に。何も得ていない。メイドアップな物語を読むよりも良いことを」
第3文。
Is there some evolutionary need that has molded our minds to seek stories?
「何かエボルーショナルな必要があるだろうか。私たちの心に物語をシークするようモールドする」
「・・・はい」
第4文。
Steven Pinker, the author of How the Mind Works, controversially tells that music confers no survival advantage but that fiction can "supply us with a mental catalogue of the fatal difficulties we might face someday and the outcome of strategies we could make use of in them."
「スティーブン・ピンカー、How the Mind Works の著者は、コントラバースリーに言う。音楽はコンファーしない。生き残る有利を。しかし、フィクションは、私たちに供給する。心のカタログで。フェイタルな困難の。私たちがいつか直面するかもしれない。そして、戦略のアウトカムを。私たちが利用できる。その中で」
かなり単語を覚えているほうです。
第5文。
Perhaps for writers of fiction the truth of this is even greater.
「多分、フィクションの作家にとって、この真実は、より偉大ですらある」
第6文。
But what does this mean for the mind?
「しかし、これは何を意味するのだろうか。精神にとって」
第7文。
Does it tell we have special systems in our brains that have evolved for the purpose of creating stories that might some day be useful in our real lives?
「それは言うだろうか。私たちが特別なシステムを持っていることを。私たちの脳の中に。エボルブした。物語を作る目的のために。いつか役に立つ。私たちの本当の人生に」
第8文。
And why is it that some people are better at making up stories than others, and if they are, are they therefore better prepared for whatever life throws at them?
「そして、なぜだろう。ある人々のほうが得意なのは。物語を作るのが。他人よりも。そして、もし彼らがそうならば、彼らはそれゆえに、よりよく準備しているのだろうか。どんな人生が彼らに投げられても」
問 This paragraph asks all of the following questions EXCEPT
あ. Why do people read and write fiction?
い. Dose the brain have a need to create stories?
う. What is the relation between music and fiction?
え. Does writing stories help us deal with real life?
英文が、このように多少難しくても、選択肢のほうは比較的易しいということは多いです。
選択肢が日本語の場合すらあります。
このように平易な選択肢が並んでいれば、それでむしろ、この英文は何について書かれているのか、理解の助けになります。
英文の内容を整理し、要約してくれています。
有難い。
この4つのうち、3つは、正しい選択肢なのですよ。
こういうことが書いてある英文なのですね。
そのつもりで見直すと、わかりにくかった英文がほぐれて、ああそういう意味か、と理解しやすくなるのです。
あ. なぜ人々はフィクションを読んだり書いたりするのか。
い. 脳は物語を創造する必要があるのだろうか。
う. 音楽とフィクションとの関係は何だろうか。
え. 物語を書くことは、私たちが現実生活に対処するのを助けるだろうか。
「答は?」
「え」
「・・・違います」
完璧でないとしても、この程度は意味を取ることができているのなら、正解しても良いはずなのに、なぜか誤答してしまう・・・。
そういう不器用なタイプの生徒もいます。
「問の This paragraph asks all of the following questions EXCEPT の意味はわかりますか?」
「・・・このパラグラフは、尋ねる。すべての以下の質問を。~を除いて」
「そうです。よくわかっているじゃないですか。つまり、この段落には、多くの疑問が提示されているのですが、あ~えの選択肢の中で、1つだけ示されていない疑問があります。それを選ぶんですよね?」
「はい」
「間違っている選択肢を選ぶ問題ですよね?正しい選択肢を選んでしまった、ということではないですよね?」
「はい」
「え. Does writing stories help us deal with real life? を訳してください」
「・・・書かれた物語は助ける。私たちを。本当の人生を処理することを」
「・・・writing stories は、書かれた物語、ではないです。書かれた物語ならば、written stories 。writing stories は、動名詞。そうすると、そこのところは、どういう意味でしょうか」
「書いている物語は・・・」
「・・・動名詞ですよ。分詞じゃないんです。耳に届いてますか?動名詞、です」
一度思い込むと、修正が効かないということは、生徒にはよくあります。
動名詞という文法事項を知らないわけではないのに、間違えるとパニックを起こして、ヒントが耳に届きにくくなります。
「動名詞です。~すること、です。物語を書くこと、です」
「ああ・・・。どう見分けるんですか」
「文脈で判断します。ストーリーさんが何かを書くわけがないので、分詞だとは思えません。だから、動名詞です」
「ああ・・・」
「物語を書くことが、私たちを助けるんです。私たちが何をすることを助けるんですか」
「本当の人生を・・・」
「・・・間違ってはいないですが、何か少し変ですね。real life は『現実生活』という意味です」
「どう見分けるんですか」
「本当の人生ならば、true life じゃないですかね」
おそらく、中学生の頃から、really を見慣れ過ぎていて、それはいつも「本当に」と訳してきたので、そこからの類推で、real life を、本当の人生、と訳してしまうのだと思います。
完全に間違っているわけではないですが、訳し方のバリエーションが不足していて、いつも1つの固定した訳しかできない子は、少しずつニュアンスのズレた訳が集まって集まって、結果として英文全体の意味がよくわからない、ということが起こりやすいです。
「deal with の意味は?」
「処理する」
「うーん・・・。では、全体の訳をもう一度」
「物語を書くことは、私たちを助ける。現実生活を処理することを」
「うーん・・・。やはり、処理するが少し気持ち悪いですね。deal with は、対処する、という意味で覚えておいほうが使いまわしが効きますよ」
「・・・」
書いてある物語は、私たちが本当の人生を処理するのを助ける。
という誤訳。
物語を書くことは、私たちが現実生活に対処するのを助ける。
という訳。
似ていますし、上の誤訳で十分正答に至ることのできる生徒もいますが、若干頭が固くて、だから、訳も固くなるタイプの子は、自分の誤訳が、本文のどこかに書いてあるとは思えず、そうすると「え」が答、となってしまうようです。
この問いかけは、第7文に書いてありました。
Does it tell we have special systems in our brains that have evolved for the purpose of creating stories that might some day be useful in our real lives?
「私たちの脳の中には、特別なシステムがあるというのだろうか / 物語を作る目的のために進化した / いつか、私たちの現実生活に役にたつかもしれない」
日本語らしい順番に並べれば、
私たちの脳の中には、いつか現実生活に役にたつかもしれない物語を作るために進化した特別なシステムがあるというのだろうか。
書いてありますね。
では、「え」は正解ではないです。
間違っているものを選ぶ四択問題は、選択肢を読んでいるうちに正しい選択肢を選んでしまうという失敗をしてしまう子が多いです。
さすがに高校生ですから、設問を読んで、間違っている選択肢を選ぶのだと一応認識しているのですが、読んでいるうちに忘れてしまうようです。
それがまず、初歩のつまずき。
次に、間違っている選択肢を選ぶということは理解しているものの、英文を読む力が弱く、本文も、選択肢も、実際のところほとんど読み通すことができない場合。
何度も書いてきましたが、本文と同じ語句が使われている選択肢が正しい選択肢、使っていなければ間違っている選択肢、という判断しかできない学力の子たちもいます。
しかし、むしろ、正しい選択肢は、本文を言い換えていることのほうが多いのです。
とはいえ、今回は、どの選択肢も、本文中に使われている言葉が入っているので、そういう観点で選択肢を選ぶことはできません。
第三段階になると、上のように、意味の取り方が固いため、本文に書かれていることとはニュアンスが異なってしまって、
「こんなことは書いていない」
と思って選んでしまう子。
単語暗記はしているのですが、1単語について1つの訳して覚えていないので、すべてが固いのです。
これは、経験不足によるところが大きいです。
教科書の英文を自分で日本語に訳して、模範の訳と照らし合わせて、正しいニュアンスの訳をつかんでいく練習。
あるいは、日本語から英語に直すことで、この日本語がこんな英語になるんだいう感覚を養っていく練習。
そういう基本の積み重ねが、初見の長文を読む際に、底力となります。
とはいえ、この問題、本文の多少の難しさとバランスをとるように、設問自体は非常に簡単です。
正解は、「う. What is the relation between music and fiction?」です。
音楽とフィクションとの間の関係は何であるか。
そんな話、してないですよね。
音楽という単語は、1回だけ出てきますが。
第4文。
Steven Pinker, the author of How the Mind Works, controversially tells that music confers no survival advantage but that fiction can "supply us with a mental catalogue of the fatal difficulties we might face someday and the outcome of strategies we could make use of in them."
「スティーブン・ピンカー、How the Mind Works の著者は、コントラバースリーに言う。音楽はコンファーしない。生き残る有利を。しかし、フィクションは、私たちに供給する。心のカタログで。フェイタルな困難の。私たちがいつか直面するかもしれない。そして、戦略のアウトカムを。私たちが利用できる。その中で」
生徒のこの訳で、十分だと思います。
音楽ができないことをフィクションは行うと語っているだけで、『関係』は語っていません。
そのことは、この訳で十分わかります。
長文読解は、どれだけ単語を覚えても、自分が第一志望とする大学や、受けようと思う英検の級では、知らない単語が出てくるのは仕方ありません。
全て知っている単語ばかりの長文は、自分にとって完全に格下レベルの長文です。
滑り止めの大学ならわかりますが、第一志望でそれはないでしょう。
英検ならば、もう1つ上の級を受けたらいいのです。
つまり、知らない単語は、問題文の中に常に出てきます。
知らない単語は英語のままで読み通していけばよいのです。
それには、常にこのような練習をしていく必要があります。
前から順番に訳すのも、そのためです。
日本語の順番に整えようとし、修飾関係を考えて訳そうとすると、負荷がかかり、混乱します。
それは、「和訳せよ」という設問のときにのみ、対応すればいいことです。
読み進めていくときに、そんなことは必要ありません。
わからない単語は、わかってみれば、どうでもいい単語のことが多いのです。
意味をちょっと強めているか、弱めているだけ。
副詞の場合は特にそうです。
それでも気になる人は、辞書ではなく、自分の単語集の索引で、わからなかった単語を引いてみるのをお勧めします。
単語集に載っているのにわからなかった単語のことは、多少反省したほうがいいです。
覚え直しましょう。
しかし、単語集にも載っていない単語なら、入試問題としては、どうでもいいと見切るのも、実践的な英語学習法です。
2024年12月13日
中1数学「反比例」と計算力。

中1の数学「比例と反比例」は、半分以上は小6の復習ですので、習得できない内容ではないはずなのですが、特に反比例の場合、計算力の壁が立ちはだかる場合があります。
まずは、計算力をそれほど問われない、簡単な問題から。
例えば、こんな問題です。
問題 y=6 / x とする。x=2 のときの y の値を求めなさい。
与えられた式に代入すればいいだけだということを、ほとんどの生徒が知っています。
y=6 / 2
=3
と、簡単に解くことができます。
しかし、以下のような問題になると、もう解けない子が現れます。
問題 y=3 / x とする。x=2/3 のときの y の値を求めなさい。
数学が苦手な子は、数の扱いが不器用であることが多く、分数の分母が分数になるときにどうしたらいいのか、もうわからないのです。
分数というのは、わり算です。
分子÷分母です。
だから、
y=3÷2/3
=3×3/2
=9/2
と、解いていくことができます。
しかし、数学が苦手な子は、「分数は、分子÷分母のわり算である」という知識が身につきません。
分母が分数になった瞬間に、計算できなくなります。
1÷3=1/ 3
こうした式を例に挙げ、分数は「分子÷分母」であることを実感で理解してもらおうとします。
そのときは、理解した顔をします。
しかし、宿題に出すと、またわからない。
「わからなかった」
と言って、解いてきません。
翌週の授業でも、もう忘れています。
なぜか、定着しないのです。
こんな問題も、数学が苦手な子は対応できません。
問題 y=3/x とする。y=2/5のときの x の値を求めなさい。
代入することはできますが、
2/5=3/x
と代入したまま、立ち往生となります。
分母が x の方程式をどう解いていいのか、わからないのです。
まずは両辺をx倍して、
2/5x=3
両辺に5/2をかけて、
x=15/2
このようにスマートに解いていける中1は、相当に数学が得意な子のみです。
実は、分数=分数 の形になったときには、もっと簡単な解き方があって、互いの分母と分子をたすきにかけて、式を変形することが可能です。
比例式を解く際の、(内項の積)=(外項の積) と同じ考え方ですが、比と分数は同じカテゴリーのものであるというのは、小学校で学習している割に定着しない学習内容です。
2/5=3/x より
2x=15
x=15/2
です。
慣れれば簡単です。
高校生になったら、特に、「三角比」の正弦定理を利用した問題を解くときに、この解き方を知っていると計算が速く正確になります。
しかし、これは、高校生でも数学が得意な子でないと定着しないことが多く、中1に教えるのはまだ早い解き方ではあります。
もっと数学が苦手な子になると、yの値が整数でも、解けなくなります。
問題 y=3/x とする。y=6のときの x の値を求めなさい。
6=3/x
までは、式を立てることができるのですが、その後、どうしていいかわからず、あてずっぽうで、
x=18
といった答を書き、それが不正解となるとさらに混乱していきます。
数の扱いと方程式の解法に習熟していないのです。
特に、分数の扱い方がわかっていません。
小学校の頃から分数が苦手で、分数は「分数」という単元が終わればもう忘れていいもの、という希望的観測で生きてきたような気配を感じます。
中1の「比例・反比例」以前の単元を学習していても、その兆候は感じます。
方程式の計算のとき、答が分数になると、
「割り切れない」
と訴えてきます。
「割り切れないときは、分数ですよ」
と説明すると、ひるんだ顔をします。
そんなことがあるとは予想していなかった。
分数の単元でもないのに、分数を出してくるなんて、卑怯だ。
・・・と、そこまで思っているかどうかはわかりませんが、とにかく、分数を使わないで数学の問題を解きたいという意志を強く感じるのです。
まだ中1くらいですと、答が整数にならないときは、小数で解いてくる子も多いです。
別に間違ってはいないですが、「データ」に関する単元のとき以外は、基本的には小数は使わず、分数で処理しましょう、小数は割り切れない、という限界がありますが、分数は全ての実数を表すことができますから。
そう説明しても、乗り気でない顔をするばかりです。
余程分数に関して苦手意識があるのでしょう。
実際、本当に数学が苦手な子になると、分数の加減乗除のやり方を忘れていることがあります。
「通分」「約分」といった言葉の意味も忘れています。
それでは分数を避けたがるだろうなあとは思うのです。
やり方をただ丸暗記して、その単元が終われば忘れて、を繰り返してきた子は、分数の計算ができないのです。
分数の計算に習熟してもらうという課題は課題として。
反比例の問題は、もっと簡単に解く方法があります。
反比例の式を答えなさいという問題ならば、フォーマルな形の、
y=a / x
で答える必要がありますが、自分で計算するときには、この形にこだわる必要はありません。
それを変形した、
xy=a
を使えば、計算はどれも簡単になります。
問題 y=3 / x とする。x=2/3 のときの y の値を求めなさい。
この場合は、xy=3 ということですから、
x=2/3 を代入して、
2/3y=3
両辺に3/2をかけて、
y=9/2
とすぐに答が出ます。
ただし、上の解き方は、できない子もいます。
その場合は、もっと段階を踏んで、
2/3y=3
両辺を3倍して、
2y=9
両辺を2で割って、
y=9/2
でも、大丈夫です。
y について解くということは、y の係数を1にするということ。
2/3はどうすれば1になるか?
逆数の3/2をかければいい。
この考え方も、数学が苦手な子にはあまり理解できない考え方なので、その理解には時間がかかります。
数理の基盤がないことが、こういう細部で露呈します。
小学校の6年間、やり方を覚えて忘れてを繰り返すのみという間違った学習を続けてきたので、そう簡単には定着しません。
しかし、絶望する必要もないのです。
高校生になる頃には、案外するっと理解できたりしますから、時機を待ちましょう。
問題 y=3/x とする。y=2/5のときの x の値を求めなさい。
これも、xy=3 の式に代入するのなら、楽に計算していけます。
2/5x=3
x=15/2
です。
このように計算すれば、計算力の乏しい子も、正解を出すことができます。
しかし、残念なことに、計算力の乏しい子、数学が苦手な子ほど、この解き方も定着しない傾向があります。
y=a / x の式にこだわらず、計算過程では、xy=a を使っていく。
その解き方を、
「あ、便利ですね」
とスッと理解し、さっと利用するのは、もともと数学が得意な子たちです。
数学が苦手な子たちは、こうした楽な解き方を解説しても、それもまたすぐに忘れ、宿題は、y=a / x の式に代入する杓子定規な解き方をしようとして上手くできず、白紙とするか、計算ミスをするか、となりがちです。
数学が得意な子と苦手な子との格差は、このようにして開いていくばかりです。
なぜ定着しないのでしょうか?
理由はその子によって色々です。
まず、便利であることは一応理解できるが、すぐに忘れてしまう子が大多数です。
記憶がもたないのです。
宿題を解く頃には、もう忘れています。
教わったことを復習してから宿題を解く、という習慣もありません。
身につかないことは、永久に身につかずに終わっていきます。
解説を黙って聞いているが、心の中で却下している子もいるのでしょう。
「学校で習っていない。学校で習っていない解き方をすると、学校の先生に目をつけられる」
そのような意識が強い場合もあれば、
「そんな解き方は良くない」
となぜか根拠のない本人の判断を絶対視しているタイプの子もいます。
「解き方を2つも覚えられない。1つだけでいい」
と思っている場合もあると思います。
数学は色々な解き方が可能な、のびやかな教科です。
それなのに、1つの解き方を丸暗記する解き方しかできない・・・。
数理の基盤が本人の中にないので、何をしても良くて何をしたらダメなのか、本人には判断できないのです。
頭が本当に硬い子になると、比例の問題でも不正解となります。
問題 y=5x とする。y=3 のときの x の値を求めなさい。
3=5x
という代入した式を立てることはできますが、その先が上手く計算できません。
5x=3
と、左辺と右辺を取り換えれば簡単な方程式ですよと助言しても、不可解なほどに、その助言には従いません。
3=5x
という方程式を睨みつけ、長考の末、
x=15
と答えたりします。
これも、「答が分数になるのは嫌だ」という感情が働いてのこともあるのでしょうが、右辺と左辺を取り換えないのは、数学が苦手な子の特徴です。
いちいち書き換えるのが面倒なら、最初から、
5x=3
と書けばいいのですが。
y=5x に y=3を代入して、
5x=3
と書いてある答案に、どこの誰がケチをつけるというのか?
でも、なぜか、
「そういうことはしてはいけない!」
と思い込んでしまうようです。
それでいて、
3=5x
と書いた後に、
5x=3
と書き換えることもしない・・・。
頭の疲れる暗算に自分を追い込み、そして間違えてしまうのです。
比例・反比例の理解よりもはるか手前の段階で、つまずいている子は多いです。
計算力が足りないのが根本ですが、それは小学校の計算ドリルや、今はあまり言われなくなった「百マス計算」で解決がつくことではない、もっと伸びやかな計算力が足りないのです。
小学生のうちに身についていてほしい数理の基盤が形成されていない・・・。
数に対する感覚が、育っていない・・・。
だから、分数をひたすら忌避するような、数学的原始人の状態に陥っています。
基盤がないから、中1の1学期に学習した「等式の性質」も、血肉となっていない。
だから、方程式の解き方が、ただの作業手順となり、そこから少しでも外れると、できなくなってしまう・・・。
数学が苦手な原因は何なのか?
どこでつまずいているのか。
まずは、その正確な分析をし、一つ一つ、克服していきましょう。
壁は、この先も、いくつもいくつも立ちはだかると思います。
しかし、全ての壁は、扉なのです。
まずは、計算力をそれほど問われない、簡単な問題から。
例えば、こんな問題です。
問題 y=6 / x とする。x=2 のときの y の値を求めなさい。
与えられた式に代入すればいいだけだということを、ほとんどの生徒が知っています。
y=6 / 2
=3
と、簡単に解くことができます。
しかし、以下のような問題になると、もう解けない子が現れます。
問題 y=3 / x とする。x=2/3 のときの y の値を求めなさい。
数学が苦手な子は、数の扱いが不器用であることが多く、分数の分母が分数になるときにどうしたらいいのか、もうわからないのです。
分数というのは、わり算です。
分子÷分母です。
だから、
y=3÷2/3
=3×3/2
=9/2
と、解いていくことができます。
しかし、数学が苦手な子は、「分数は、分子÷分母のわり算である」という知識が身につきません。
分母が分数になった瞬間に、計算できなくなります。
1÷3=1/ 3
こうした式を例に挙げ、分数は「分子÷分母」であることを実感で理解してもらおうとします。
そのときは、理解した顔をします。
しかし、宿題に出すと、またわからない。
「わからなかった」
と言って、解いてきません。
翌週の授業でも、もう忘れています。
なぜか、定着しないのです。
こんな問題も、数学が苦手な子は対応できません。
問題 y=3/x とする。y=2/5のときの x の値を求めなさい。
代入することはできますが、
2/5=3/x
と代入したまま、立ち往生となります。
分母が x の方程式をどう解いていいのか、わからないのです。
まずは両辺をx倍して、
2/5x=3
両辺に5/2をかけて、
x=15/2
このようにスマートに解いていける中1は、相当に数学が得意な子のみです。
実は、分数=分数 の形になったときには、もっと簡単な解き方があって、互いの分母と分子をたすきにかけて、式を変形することが可能です。
比例式を解く際の、(内項の積)=(外項の積) と同じ考え方ですが、比と分数は同じカテゴリーのものであるというのは、小学校で学習している割に定着しない学習内容です。
2/5=3/x より
2x=15
x=15/2
です。
慣れれば簡単です。
高校生になったら、特に、「三角比」の正弦定理を利用した問題を解くときに、この解き方を知っていると計算が速く正確になります。
しかし、これは、高校生でも数学が得意な子でないと定着しないことが多く、中1に教えるのはまだ早い解き方ではあります。
もっと数学が苦手な子になると、yの値が整数でも、解けなくなります。
問題 y=3/x とする。y=6のときの x の値を求めなさい。
6=3/x
までは、式を立てることができるのですが、その後、どうしていいかわからず、あてずっぽうで、
x=18
といった答を書き、それが不正解となるとさらに混乱していきます。
数の扱いと方程式の解法に習熟していないのです。
特に、分数の扱い方がわかっていません。
小学校の頃から分数が苦手で、分数は「分数」という単元が終わればもう忘れていいもの、という希望的観測で生きてきたような気配を感じます。
中1の「比例・反比例」以前の単元を学習していても、その兆候は感じます。
方程式の計算のとき、答が分数になると、
「割り切れない」
と訴えてきます。
「割り切れないときは、分数ですよ」
と説明すると、ひるんだ顔をします。
そんなことがあるとは予想していなかった。
分数の単元でもないのに、分数を出してくるなんて、卑怯だ。
・・・と、そこまで思っているかどうかはわかりませんが、とにかく、分数を使わないで数学の問題を解きたいという意志を強く感じるのです。
まだ中1くらいですと、答が整数にならないときは、小数で解いてくる子も多いです。
別に間違ってはいないですが、「データ」に関する単元のとき以外は、基本的には小数は使わず、分数で処理しましょう、小数は割り切れない、という限界がありますが、分数は全ての実数を表すことができますから。
そう説明しても、乗り気でない顔をするばかりです。
余程分数に関して苦手意識があるのでしょう。
実際、本当に数学が苦手な子になると、分数の加減乗除のやり方を忘れていることがあります。
「通分」「約分」といった言葉の意味も忘れています。
それでは分数を避けたがるだろうなあとは思うのです。
やり方をただ丸暗記して、その単元が終われば忘れて、を繰り返してきた子は、分数の計算ができないのです。
分数の計算に習熟してもらうという課題は課題として。
反比例の問題は、もっと簡単に解く方法があります。
反比例の式を答えなさいという問題ならば、フォーマルな形の、
y=a / x
で答える必要がありますが、自分で計算するときには、この形にこだわる必要はありません。
それを変形した、
xy=a
を使えば、計算はどれも簡単になります。
問題 y=3 / x とする。x=2/3 のときの y の値を求めなさい。
この場合は、xy=3 ということですから、
x=2/3 を代入して、
2/3y=3
両辺に3/2をかけて、
y=9/2
とすぐに答が出ます。
ただし、上の解き方は、できない子もいます。
その場合は、もっと段階を踏んで、
2/3y=3
両辺を3倍して、
2y=9
両辺を2で割って、
y=9/2
でも、大丈夫です。
y について解くということは、y の係数を1にするということ。
2/3はどうすれば1になるか?
逆数の3/2をかければいい。
この考え方も、数学が苦手な子にはあまり理解できない考え方なので、その理解には時間がかかります。
数理の基盤がないことが、こういう細部で露呈します。
小学校の6年間、やり方を覚えて忘れてを繰り返すのみという間違った学習を続けてきたので、そう簡単には定着しません。
しかし、絶望する必要もないのです。
高校生になる頃には、案外するっと理解できたりしますから、時機を待ちましょう。
問題 y=3/x とする。y=2/5のときの x の値を求めなさい。
これも、xy=3 の式に代入するのなら、楽に計算していけます。
2/5x=3
x=15/2
です。
このように計算すれば、計算力の乏しい子も、正解を出すことができます。
しかし、残念なことに、計算力の乏しい子、数学が苦手な子ほど、この解き方も定着しない傾向があります。
y=a / x の式にこだわらず、計算過程では、xy=a を使っていく。
その解き方を、
「あ、便利ですね」
とスッと理解し、さっと利用するのは、もともと数学が得意な子たちです。
数学が苦手な子たちは、こうした楽な解き方を解説しても、それもまたすぐに忘れ、宿題は、y=a / x の式に代入する杓子定規な解き方をしようとして上手くできず、白紙とするか、計算ミスをするか、となりがちです。
数学が得意な子と苦手な子との格差は、このようにして開いていくばかりです。
なぜ定着しないのでしょうか?
理由はその子によって色々です。
まず、便利であることは一応理解できるが、すぐに忘れてしまう子が大多数です。
記憶がもたないのです。
宿題を解く頃には、もう忘れています。
教わったことを復習してから宿題を解く、という習慣もありません。
身につかないことは、永久に身につかずに終わっていきます。
解説を黙って聞いているが、心の中で却下している子もいるのでしょう。
「学校で習っていない。学校で習っていない解き方をすると、学校の先生に目をつけられる」
そのような意識が強い場合もあれば、
「そんな解き方は良くない」
となぜか根拠のない本人の判断を絶対視しているタイプの子もいます。
「解き方を2つも覚えられない。1つだけでいい」
と思っている場合もあると思います。
数学は色々な解き方が可能な、のびやかな教科です。
それなのに、1つの解き方を丸暗記する解き方しかできない・・・。
数理の基盤が本人の中にないので、何をしても良くて何をしたらダメなのか、本人には判断できないのです。
頭が本当に硬い子になると、比例の問題でも不正解となります。
問題 y=5x とする。y=3 のときの x の値を求めなさい。
3=5x
という代入した式を立てることはできますが、その先が上手く計算できません。
5x=3
と、左辺と右辺を取り換えれば簡単な方程式ですよと助言しても、不可解なほどに、その助言には従いません。
3=5x
という方程式を睨みつけ、長考の末、
x=15
と答えたりします。
これも、「答が分数になるのは嫌だ」という感情が働いてのこともあるのでしょうが、右辺と左辺を取り換えないのは、数学が苦手な子の特徴です。
いちいち書き換えるのが面倒なら、最初から、
5x=3
と書けばいいのですが。
y=5x に y=3を代入して、
5x=3
と書いてある答案に、どこの誰がケチをつけるというのか?
でも、なぜか、
「そういうことはしてはいけない!」
と思い込んでしまうようです。
それでいて、
3=5x
と書いた後に、
5x=3
と書き換えることもしない・・・。
頭の疲れる暗算に自分を追い込み、そして間違えてしまうのです。
比例・反比例の理解よりもはるか手前の段階で、つまずいている子は多いです。
計算力が足りないのが根本ですが、それは小学校の計算ドリルや、今はあまり言われなくなった「百マス計算」で解決がつくことではない、もっと伸びやかな計算力が足りないのです。
小学生のうちに身についていてほしい数理の基盤が形成されていない・・・。
数に対する感覚が、育っていない・・・。
だから、分数をひたすら忌避するような、数学的原始人の状態に陥っています。
基盤がないから、中1の1学期に学習した「等式の性質」も、血肉となっていない。
だから、方程式の解き方が、ただの作業手順となり、そこから少しでも外れると、できなくなってしまう・・・。
数学が苦手な原因は何なのか?
どこでつまずいているのか。
まずは、その正確な分析をし、一つ一つ、克服していきましょう。
壁は、この先も、いくつもいくつも立ちはだかると思います。
しかし、全ての壁は、扉なのです。
2024年12月04日
高校数学B「統計的な推測」二項分布の平均と分散。

数B「統計的な推測」は、旧課程の頃は、この単元丸ごと学習しない高校が多かったのです。
しかし、新課程になり、大学入試共通テストの範囲が数学B・Cとなってからは、文系の生徒が数学Cの「複素数平面」で受験するよりは、「統計的な推測」のほうがまだ理解しやすいのではないかという判断からか、高校でも扱う学校が増えてきました。
同時に、あまりのわかりにくさに悲鳴も上がっています。
公式を理解し、覚えてしまえばあとは簡単なのですが、数Ⅰ「データの分析」のときから、統計に苦手意識があり、どうにも公式が理解しづらい様子です。
そもそも、用語がわかりづらい・・・。
聞いたことのない用語が一気に出てくるので、それで面食らう、ということがあるようです。
これは、覚えるしかないので、用語の意味がわからなくなったら、逐一、定義に戻って意味を確認してください。
とはいえ、定義もかなり難しい・・・。
まず、二項分布の定義から見ていきましょう。
1回の試行で事象Aの起こる確率が p である独立試行を n 回繰り返し、Aの起こる回数を確率変数 X とすると、
P(X=r)
=nCr・p^r(1-p)^n-r
である。
このとき、Xの確率分布を二項分布といい、
B(n , p )
で表す。
平均は、
E(X)=np
分散は、
V(X)=np(1-p)
標準偏差は、
σ(X)=√np(1-p)
である。
・・・何、それ?
まずは、具体的に考えてみましょう。
問題 1個のさいころを5回投げるとき、3の目が出る回数を X とする。確率変数 X の平均と標準偏差を求めよ。
これは、数Aで学習した、反復試行の確率の問題と似ていますよね。
反復試行は、大丈夫でしょうか?
というわけで、反復試行の確率の問題を復習しておきましょう。
復習問題 1個のさいころを5回投げるとき、3の目が2回出る確率を求めよ。
このように、同じ試行を繰り返していく場合の確率が、反復試行の確率です。
さいころを5回投げるとき、3の目が2回出る・・・。
具体的に考えます。
まず、単純に、1回目と2回目に3の目が出て、以降は3以外の目が出たのだとしてみましょう。
その確率は、
1/6・1/6・5/6・5/6・5/6
しかし、これだけでは、1回目と2回目に3が出た場合のみの確率です。
3の目が2回出るのは、1回目と2回目に出る場合だけではありません。
1回目と3回目に3が出て、他はそれ以外の目。
2回目と3回目に3が出て、他はそれ以外の目。
・・・など、複数の出方があります。
その全ての場合で、それぞれの確率は、
1/6・1/6・5/6・5/6・5/6
です。
そして、それらの目の出方は、互いに排反。
すなわち、かぶりませんから、確率を足せばいいのだとわかります。
では、5回のうち、3の目が2回だけ出る場合の数は?
それは、5回のうち、3の目が出る2か所を選ぶ場合の数と考えられますから、組み合わせの公式を用いて、
5C2
となります。
したがって、1個のさいころを5回投げるとき、3の目が2回出る確率は、
5C2・(1/6)^2・(5/6)^3
という式で求めることができます。
これが、反復試行の確率の求め方です。
では、少しずつ、一般化しましょう。
さいころを n 回投げて、3の目が r 回出る確率は、
nCr・(1/6)^r・(5/6)^n-r
さらに一般化しましょう。
さいころから離れ、3の目からも離れます。
1回の試行で事象Aが起こる確率が p である独立試行を n 回繰り返すとき、Aの起こる回数が r 回である確率は、
nCr・p^r・(1-p)^n-r
ここまで、いいでしょうか?
さて、そこで、二項分布の定義を見直しましょう。
1回の試行で事象Aの起こる確率がpである独立試行を n 回繰り返し、Aの起こる回数を確率変数 X とすると、
P(X=r)
=nCr・p^r(1-p)^n-r
である。
このとき、Xの確率分布を二項分布といい、
B(n , p )
で表す。
これが定義です。
P(X=r) というのは、この「統計的な推測」という単元の一番最初に学習した表し方でした。
X が r のときの確率、という意味でした。
ということは、書き方が少し複雑なだけで、これは、反復試行の公式そのままです。
確率が、反復試行の公式をそのまま使うことになることが明白な場合、きっと確率の分布に何かルールがあるぞ、ということは推測できます。
こういう形の確率分布を、二項分布と呼ぶ、というのが、まずは定義です。
・・・なぜ二項という名前を使うのか?
というと、それは、数Ⅱで学習した「二項定理」が関係しているのです。
二項定理は覚えているでしょうか。
こういうものでした。
例えば、
(x+3)^5=5C0・x^5+5C1・x^4・3+5C2・x^3・3^2+5C3・x^2・3^3+5C4・x・3^4+5C5・3^5
=x^5+3x^4+90x^3+270x^2+405x+243
公式は、
(p+q)^n=nC0・p^n+nC1・p^n-1・q+nC2・p^n-2・q^2+・・・+nCn-1・pq^n-1+nCn・q^n
・・・何か似てる!
反復試行の確率の公式に似てる!
というか、そっくりです。
だから、二項分布という名前なのです。
何か知らないけど、そう呼ぶのだな、という把握で、今は大丈夫です。
とりあえず、反復試行の確率の確率分布を、二項分布と呼びます。
そして、B(n , p)で表します。
・・・なぜB?
「二項分布」は、英語で、binominal distribution と呼びます。
その頭文字のBです。
B(n , p)
Bは、「これは二項分布、つまり反復試行の確率の確率分布ですよー」という合図。
そして、試行回数はnですよー。
1回の試行で、ある事象Aが起こる確率はpですよー。
そういう意味です。
そして、n と p、その2つの数値さえわかれば、反復試行の確率の式は立つのです。
重要な数値は、この2つ。
これで確率分布は決まるよー。
そういう意味だと、ざっくりとらえれば、大丈夫です。
さて、ここまで、まあ何とか呑み込んだとして。
ここからが重要。
3本の公式が出てきます。
平均は、
E(X)=np
分散は、
V(X)=np(1-p)
標準偏差は、
σ(X)=√np(1-p)
この公式が、あまりにもシンプル過ぎて、逆に意味がわからない・・・。
そういう悩みがあるかと思います。
なぜ、X の平均、すなわち期待値が、npで出るのか?
何で、そこがかけ算なのか?
どういう意味?
でも、これも、現実に即して考えれば、当たり前です。
例えば、こんな例で考えてみましょう。
例 1個のさいころを6回投げるとき、2の目は何回出ると期待できるか?
2の目がX 回出るとしましょう。
さいころの目は6種類あります。
そのうちの2の目は、6回投げたら、1回くらいは出ると期待できるんじゃないでしょうか。
6回に1回。
1/6の確率なのですから、6回に1回は出てもいいでしょう。
これがまさに、二項分布B(6 , 1/6) において、
E(X)=np=6・1/6=1
です。
公式と感覚が完全に一致します。
X は、この例では、1個のさいころを6回投げるのとき、2の目が X 回出る、という意味の X です。
X は確率変数ですので、何種類かの値を取ります。
今、さいころを6回投げていますから、Xは、
X=0 , 1 , 2 , 3 , 4 , 5 , 6
の7通りが考えられますが、
6回も投げたのに、2の目が0回ということは、そんなにあることではない。(勿論、実際はありえます)
6回も投げて、6回とも2の目ということも、そんなにあることではない。(勿論、これも可能性はあります)
実際のところ、1回投げるごとの、2の目が出る確率は1/6なのだから、その1/6が、集まって集まって集まって、
1/6+1/6+1/+1/6+1/6+1/6
=1/6・6
=1
となり、6回投げたら、1回くらいは2の目が出ると期待できる。
2の目が出る平均の回数は、1回である。
そういう意味でとらえれば、この公式は、するっと頭に入ると思います。
式として、比較的しっかりと証明するならば、
1回の試行で事象Aの起こる確率を p とする。
この試行を n 回繰り返すとき、
第 k 回の試行でAが起これば1、起こらなければ0の値をとる確率変数をXk とする。
・・・ついてきてますかー?
k=0,1,2,3,・・・,n
となります。
そのそれぞれで、実際に A という事象が起これば1、起こらなければ0の値を取ります。
ここも難しいところです。
期待値のこれまでの学習と混ざって、kの値×確率pではないのか、という混乱が起こりそうですが、実際には、そんなかけ算はあり得ません。
k は、第 k 回の試行というだけの数字なので、2回目だから急に値が2に増えるということはありません。
第何回でも、平等に、事象 A が起これば1、起こらなければ0。
そうとらえます。
このとき、
P(Xk=1)=p、P(Xk=0)=q (q=1-p)
です。
これも書き方が難しいですが、
Xkが1である、すなわち第k回目に、Aという事象が起こる確率は、pである。
Xkが0である、すなわち第k回目に、Aという事象が起こらない確率は、q (ただしq=1-p)。
ということです。
となると、k 回目にAという事象が起こる期待値は、
E(Xk=1)=1・p+0・q=p
となります。
で、実際に、X1 や X2 が1になるか0になるかは、そのとき次第ですが、
X=X1+X2+X3+X4+・・・+Xn
とおくと、この X は、n 回のうち A が起こる回数ということですから、その平均、すなわち期待値は、
E(X)=E(X1)+E(X2)+E(X3)+・・・+E(Xn)
=p+p+p+・・・+p
=np
となります。
実感は簡単なのに、証明するとなると難しい・・・。
次に課題となるのが、分散の公式の意味です。
分散は、
V(X)=np(1-p)
これも、もう諦めてこのまま覚えますというのなら、それでも良いと思うのですが、やはり、それでは不安定で、覚えづらく、脳からすぐ消えていきそうな気がします。
一度はしっかりと、理解しておきたい。
分散の公式は大丈夫でしょうか?
数Ⅰ「データの分析」で分散を学習したときに、定義通りの1本目の公式しか覚えなかった人もいると思いますが、分散の公式は、2本目のほうが使い道があるのです。
数学の公式は、大体そうです。
2本あるときは、2本目に意味があります。
難しい問題ほど、2本目のほうが威力を発揮します。
分散の公式の2本目とは、
分散=2乗の値の平均値-平均の2乗
という公式です。
V(X)=E(X^2)-{E(X)}^2
ここで、平均と期待値は同じ意味だということも、改めて把握しましょう。
平均でどれくらいなのかと、どれくらい期待できるのかは、同じ意味です。
したがって、
分散=(X^2の期待値)-(Xの期待値)^2
となります。
さきほど、
E(Xk)=1・p+0・q=p
でした。
また、
E(Xk^2)=1^2・p+0^2・q=p
となります。
よって、
V(Xk)=E(Xk^2)-{E(Xk)}^2
=p-p^2
=p(1-p)
=pq
つまり、
V(X1)=pq
ですし、
V(X2)=pq
です。
ここで、確率変数X1,X2,X3,・・・Xnは互いに独立だから、
V(X)=V(X1)+V(X2)+V(X3)+・・・+V(Xn)
=pq+pq+pq+・・・+pq
=npq
=np(1-p)
となります。
標準偏差は、分散の正の平方根のことですので、証明は不要ですね。
何とか呑み込んだら、後は、使うのみです。
問題に戻りましょう。
問題 1個のさいころを5回投げるとき、3の目が出る回数をXとする。確率変数Xの平均と標準偏差を求めよ。
さいころを1回投げて3の目が出る確率は1/6。
明らかに反復試行ですので、確率変数 X は、二項分布 B(5 , 1/6) に従います。
平均というのは期待値のことですから、
E(X)=np=5・1/6=5/6
よって、平均は、5/6。
分散は、
V(X)=npq
=5・1/6・5/6
=25/36
標準偏差は、分散の正の平方根ですから、
σ=√25/36=5/6
標準偏差は、5/6 です。























