2021年08月07日
夏休みは難問を。二等辺三角形と3つの内接円の問題。
問題 3辺の長さがそれぞれ10、10、12である二等辺三角形があり、3つの円がその内側にある。3つの円は図のように、それぞれ各辺に接し、またお互いに接している。3つの円の半径の長さを求めよ。
さて、この問題、10秒と経たずに解法に気づく人もいると思いますが、パっとみて気づかないと、かなりハマることになる問題です。
該当学年は中3。
単元は「平面図形と三平方の定理」です。
この問題、外側の三角形が正三角形の場合は、少し発展的な問題集には必ず載っている典型題です。
相似な三角形と三平方の定理で解くことが可能です。
むしろ、その印象が強すぎると、そこにとらわれて、ひどく複雑な連立方程式を立てることになり、何時間でもうなってしまうことになります。
こんな問題、成立するの?
二等辺三角形の中に、3つの内接円なんて描けないんじゃないの?
と疑問を抱くことになるほどハマる場合もあるかと思います。
夏休みで、時間も十分ありますので、数学の問題を楽しみたいと思う方は、ここでいったん図だけを書き写し、このブログを読むのをやめて、この問題に挑戦していただければと思います。
さて、ここからは解決編です。
まず、二等辺三角形の対称性から、円O2とO3は、半径が等しい合同な円だということがわかります。
二等辺三角形の頂角の二等分線は底辺を垂直に2等分します。
その二等分線は、円O1の中心を通り、円O2とO3の接点を通ります。
その二等分線で、この三角形を半分に切りましょう。
下の図が、半分に切った三角形の左側です。
直角三角形となります。
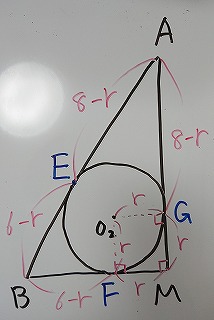
三平方の定理により、3辺の長さは6、8、10となります。
そこに、円O2だけを描くと、問題は極めてシンプルであることがわかると思います。
円O2の半径をrとします。
円と接線の定理を使えます。
円外の点から、その円へは2本の接線がひけます。
円外のその点から接点までの距離は等しいです。
図では、長さ6の辺の、円との接点から直角の頂点のところまでが、円の半径と等しく、rとなります。
すると、長さ6の辺の残りの部分BFは、6-r。
長さ8の辺の、線分MGも、rです。
すると、長さ8の辺の残りの部分AGは、8-r。
したがって、
長さ10の辺の、BEは、6-r。
長さ10の辺の、AEは、8-r。
その和が10ですから、
(6-r)+(8-r)=10
14-2r=10
-2r=-4
r=2
よって、円O2の半径は2です。
合同な円なので、円O3の半径も2です。
この発想をパッと見た瞬間に思いつくことさえできたら、この問題は何でもないのですが、このことに気づかないと、延々と苦しむことになります。
これがわかれば、円O1は、計算が多少面倒くさいだけで、発想は難しくないと思います。

他にもっとスマートな解き方があるかもしれませんが、地道な解き方としては、上の図の直角三角形O1O2Gで、三平方の定理を用いて方程式を立てましょう。
そのために、O1Gの長さを文字を使って表すことが必要です。
それには、まず、円O1の左半分も書き込んで考えます。
円O1の半径をxとします。
円O1の中心と円O1の接点Dを結びます。
それによって作られた小さな三角形ADO1は、直角三角形。
2組の角がそれぞれ等しいことから、全体の三角形と相似です。
辺の比は、短い辺から順に、3: 4:5。
したがって、AO1の長さは、5/3x。
また、GMの長さは円O2の半径と等しいので、2です。
よって、
O1G=8-5/3 x-2
=6-5/3 x
三平方の定理により、
(6-5/3 x)2+2^2=(x+2)2
展開して整理しましょう。
36-20x+25/9 x2+4=x2+4x+4
25/9 x2-24x+36=0
25x2-24・9x+36・9=0
4x2-54x+81=0
解の公式で解きます。
x=27±√(27^2-324) / 4
=27±√405 / 4
=27±9√5 / 4
0<x<6より
x=27-9√5 / 4
よって、円O1の半径は、27-9√5 / 4 です。
さて、この問題、10秒と経たずに解法に気づく人もいると思いますが、パっとみて気づかないと、かなりハマることになる問題です。
該当学年は中3。
単元は「平面図形と三平方の定理」です。
この問題、外側の三角形が正三角形の場合は、少し発展的な問題集には必ず載っている典型題です。
相似な三角形と三平方の定理で解くことが可能です。
むしろ、その印象が強すぎると、そこにとらわれて、ひどく複雑な連立方程式を立てることになり、何時間でもうなってしまうことになります。
こんな問題、成立するの?
二等辺三角形の中に、3つの内接円なんて描けないんじゃないの?
と疑問を抱くことになるほどハマる場合もあるかと思います。
夏休みで、時間も十分ありますので、数学の問題を楽しみたいと思う方は、ここでいったん図だけを書き写し、このブログを読むのをやめて、この問題に挑戦していただければと思います。
さて、ここからは解決編です。
まず、二等辺三角形の対称性から、円O2とO3は、半径が等しい合同な円だということがわかります。
二等辺三角形の頂角の二等分線は底辺を垂直に2等分します。
その二等分線は、円O1の中心を通り、円O2とO3の接点を通ります。
その二等分線で、この三角形を半分に切りましょう。
下の図が、半分に切った三角形の左側です。
直角三角形となります。

三平方の定理により、3辺の長さは6、8、10となります。
そこに、円O2だけを描くと、問題は極めてシンプルであることがわかると思います。
円O2の半径をrとします。
円と接線の定理を使えます。
円外の点から、その円へは2本の接線がひけます。
円外のその点から接点までの距離は等しいです。
図では、長さ6の辺の、円との接点から直角の頂点のところまでが、円の半径と等しく、rとなります。
すると、長さ6の辺の残りの部分BFは、6-r。
長さ8の辺の、線分MGも、rです。
すると、長さ8の辺の残りの部分AGは、8-r。
したがって、
長さ10の辺の、BEは、6-r。
長さ10の辺の、AEは、8-r。
その和が10ですから、
(6-r)+(8-r)=10
14-2r=10
-2r=-4
r=2
よって、円O2の半径は2です。
合同な円なので、円O3の半径も2です。
この発想をパッと見た瞬間に思いつくことさえできたら、この問題は何でもないのですが、このことに気づかないと、延々と苦しむことになります。
これがわかれば、円O1は、計算が多少面倒くさいだけで、発想は難しくないと思います。

他にもっとスマートな解き方があるかもしれませんが、地道な解き方としては、上の図の直角三角形O1O2Gで、三平方の定理を用いて方程式を立てましょう。
そのために、O1Gの長さを文字を使って表すことが必要です。
それには、まず、円O1の左半分も書き込んで考えます。
円O1の半径をxとします。
円O1の中心と円O1の接点Dを結びます。
それによって作られた小さな三角形ADO1は、直角三角形。
2組の角がそれぞれ等しいことから、全体の三角形と相似です。
辺の比は、短い辺から順に、3: 4:5。
したがって、AO1の長さは、5/3x。
また、GMの長さは円O2の半径と等しいので、2です。
よって、
O1G=8-5/3 x-2
=6-5/3 x
三平方の定理により、
(6-5/3 x)2+2^2=(x+2)2
展開して整理しましょう。
36-20x+25/9 x2+4=x2+4x+4
25/9 x2-24x+36=0
25x2-24・9x+36・9=0
4x2-54x+81=0
解の公式で解きます。
x=27±√(27^2-324) / 4
=27±√405 / 4
=27±9√5 / 4
0<x<6より
x=27-9√5 / 4
よって、円O1の半径は、27-9√5 / 4 です。
Posted by セギ at 13:15│Comments(2)
│算数・数学
この記事へのコメント
O₁Mではなく、O₁Gの長さです。O₁Gの長さを求められていますが、表記がO₁Mになっています。
Posted by あー at 2022年02月09日 18:45
ご指摘ありがとうございました。
Posted by セギ at 2022年03月01日 17:55
at 2022年03月01日 17:55
 at 2022年03月01日 17:55
at 2022年03月01日 17:55※このブログではブログの持ち主が承認した後、コメントが反映される設定です。



























