2020年06月30日
小学校算数。点対称の図形。
「対称な図形」は、小学校6年生で学習する単元です。
教科書によるのですが、この単元が6年生の教科書の冒頭にあり、しかも、学校が休校のため、これを独学するのが宿題だった子も多かったようです。
なお、三鷹市で採択されている教科書では、最初の単元が「ならべ方・組み合わせ方」でした。
樹形図の描き方は、手取り足取りで教えないと中学生でもなかなか定着しないのに大丈夫なのかしらと、これも心配でした。
そして、登校が始まったらあっという間に1つの単元が終了し、カラーテストを受けることとなり、苦労した子も今年は多いようです。
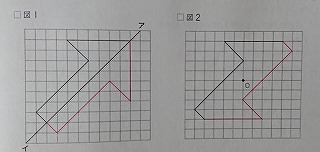
さて、まずは、線対称。
折り紙のように真ん中で折り重ねたとき、ぴったりと重なる図形が、線対称な図形です。
方眼紙に線対称な図形の半分が描かれていて、残り半分を完成させる問題が典型題です。
対称の軸が方眼紙上に垂直または水平に引かれている場合は、易しいです。
これは、理解できない子はほとんどいません。
ところが、上の図1のように、対称の軸が斜めになると、少し混乱する子が現れます。
完成図を正しくイメージすることができないのです。
頭の中に誤ったイメージが浮かびやすく、それが邪魔になる様子です。
例題などで最初に練習した問題の対象の軸が垂直方向だったため、対応する点や線分はすべて水平移動だと思い込んでしまう場合があります。
上の図1でいえば、矢印の先端部分の線分が、水平移動だと思い込むのです。
「・・・方眼紙から飛び出すけど、いいですか」
という質問をするので、え?と思い、その子がどういう誤解をしているのか気づくことがあります。
図1で、水平方向の線分は、対称移動すると垂直方向の線分になります。
それをイメージできないのです。
図形のイメージ力は個人差が大きいです。
頭の中に描くイメージだけで図を完成させられる子もいます。
しかし、本人のイメージ力が弱い、あるいは誤謬が多い場合は、想像するだけでは図を完成させることができません。
その場合は、理屈で図を完成させればよいのです。
それは「逃げ」ではありません。
線対称の図形の性質を正しく使用して作図するのですから、それもまた数学的な態度です。
では、線対称な図形の性質とは何か?
①対応する辺の長さは等しい。
②対応する角の大きさは等しい。
③対応する点を結んだ線分は、対称の軸と垂直に交わる。
④対応する点と対称の軸との距離は等しい。
これらの性質を利用し、図中に描かれている点を対称移動することで、残り半分を描いていきます。
上の図1でいえば、一番上の「矢印のてっぺんの点」は、対称の軸上にある点なので、移動せず、そのままです。
いや、完成図が「矢印」になるとわかっている時点で正しいイメージができているのですが、それは説明のための方便としてお許しください。
てっぺんから「左に5」だけ移動した位置にある点を正しく打ち込めるかが、最初の鍵です。
対称の軸が方眼紙に垂直だろうが斜めだろうが、対応する点を水平に移動させる間違ったイメージが邪魔をします。
その最初の点を打ち間違えたら、もう残りはぐちゃぐちゃです。
方眼紙に描く場合でも、定規をあてるとかなり楽になります。
理想は三角定規ですが、おそらく道具袋の奥にあり、探すのが大変でしょうから、普通の定規で大丈夫です。
短い定規は、ペンケースに常に入れておくと便利です。
その定規を、対称の軸と垂直の位置におきます。
大体で構いません。
対称移動する方向さえ見えてくればよいのです。
矢印のてっぺんから「左に5」の位置にある点は、どこに移動するか?
予想外に下のほうに移動するのだと、定規を使うことでイメージできます。
距離は?
対応する点と対称の軸との距離はそれぞれ等しいのだから、大体このあたりの点?
では、正確には?
対応する辺の長さは等しいのだから、てっぺんの点から下に5の位置?
これで正確な点の位置が判断できます。
この点を1つ打ち、てっぺんの点と結べば、残りのイメージは正確に描ける子が多いです。
ああ、こういう向きだったのかあ。
わかったー。
感動の声を上げて、残りは自力で描きあげていきます。
しかし、イメージ力には個人差があり、それでもその先をイメージできない子も中にはいます。
その場合は、次の点も、上と同じ作業を繰り返し、定規をあてて、対称移動した先のおおよその位置を特定していきます。
線対称の場合は、上の作業で大多数の子が描けるようになりますが、点対称の場合は、もっと苦闘する場合があります。
図2を見てください。
描かれている半分は図1と同じですが、完成される図は「矢印」ではありません。
「矢印を描く」という固定観念にしばられ、完成イメージを思い描けない子が多いです。
点対称の図を描いているつもりでも、途中から線対称の「矢印」を描き始めてしまうのです。
正しい点を打っているのに、矢印にならないことに混乱してしまう子もいます。
完成させるべき図は矢印ではないのに、矢印を描こうとして苦闘するのです。
図2の問題は、大人の人でも苦戦される方がいらっしゃると思います。
何の手がかりもなく、上の図2を見ただけで点対称の図形の完成図をイメージできる人のほうがむしろ少ないでしょう。
それは特別なイメージ力を持っている方だと思います。
しかし、そんな特別な才能を持っていなくても、点対称の図形を完成させることはできます。
こちらも、点対称の図形の性質を使えば、正しく作図できます。
では、点対称な図形の性質とは何か?
①対応する辺の長さは等しい。
②対応する角の大きさは等しい。
③対応する点を結んだ線分は、対称の中心を通る。
④対応する点と対称の中心との距離は等しい。
つまり、これも、定規を使用すれば、正しい位置に対応する点を打っていくことが可能です。
まず、移動したい点と対称の中心を直線で結びます。
その直線上のどこかに、対応する点があります。
対応すると点と対称の中心との距離は等しいです。
どの点から始めても大丈夫ですが、点Oに近いところから始めたほうが混乱を避けられると思います。
まず、点Oから上に2の位置にある点から移動しましょう。
その点と点Oとを結んだ直線は、方眼の垂直方向の直線です。
距離は、点Oから2。
よって、点Oから下に2の位置にこの点は移動します。
ここからは何通りかのやり方がありますが、移動した点から次の点に移動するほうが楽かもしれません。
最初に注目した点から、次の点は、左に2、上に2だけ移動した位置にあります。
点対称は180度回転するのですから、移動後の点から右に2、下に2だけ移動したのが次の点です。
点を打ったら、すぐに前の点と結び、線分を明らかにしておきましょう。
点だけ先に全部打って後で結ぼうとすると、間違った点どうしを結んでしまい、混乱を助長させてしまう可能性があるのです。
移動前の点と移動後の点に定規を当て、ちゃんと対称の中心を通っているかも確認します。
この繰り返しで点を移動していくと、徐々に図形が見えてきます。
完成図のおおよそがイメージできるようになったら、上の作業を省略し、自分の力で次の点を打っていっても大丈夫でしょう。
ときどき定規を当て、対応する点を結んだ線分が対称の中心を通っているか確認すれば、さらに間違いないです。
そのようにして完成した図が、下の図となります。
Posted by セギ at 13:24│Comments(0)
│算数・数学
※このブログではブログの持ち主が承認した後、コメントが反映される設定です。


























